3.4 实际问题与一元一次方程(配套与工程问题(第1课时))课件(PPT27张)
文档属性
| 名称 | 3.4 实际问题与一元一次方程(配套与工程问题(第1课时))课件(PPT27张) |  | |
| 格式 | rar | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-04 09:31:43 | ||
图片预览








文档简介
(共27张PPT)
义务教育教科书 数学 七年级 上册
3.4实际问题与一元一次方程
配套问题和工程问题
第1课时
1.会通过列方程解决“配套问题”和“工程问题”
2.掌握列方程解决实际问题的一般步骤
3.通过列方程解决实际问题的过程,体会建模思想
学习目标
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
复习导入
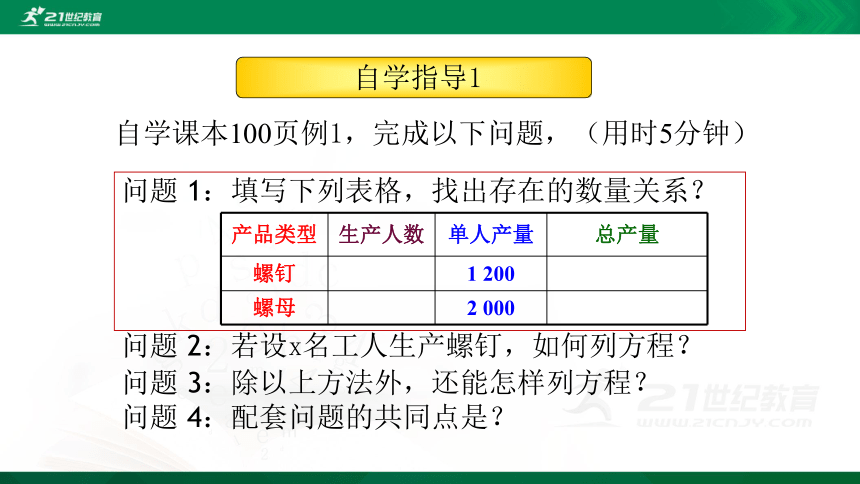
自学课本100页例1,完成以下问题,(用时5分钟)
问题 1:填写下列表格,找出存在的数量关系?
问题 2:若设x名工人生产螺钉,如何列方程?
问题 3:除以上方法外,还能怎样列方程?
问题 4:配套问题的共同点是?
自学指导1
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
列表分析:
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
22﹣x
2 000(22-x)
1 200 x
x
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x
解方程,得: 5(22-x)=6x
110-5x=6x
x=10
生产螺母有:22-x=12(人)
答:应安排10名工人生产螺钉,12名工人生产螺母.
问题3:以上问题还有其他的解决方法吗?
如果设生产螺母的有x人,那方程应该怎么列呢?用上面那个解题的思路来做一下吧!
解:设生产螺母的有x人,生产螺钉的人有(22-x)人,由题意得:
2000x=2×1200×(22-x)
x
22﹣x
2000x
1200(22-x)
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
自学课本100页例1,完成以下问题,(用时5分钟)
问题 1:填写下列表格,找出存在的数量关系?
问题 2:若设x名工人生产螺钉,如何列方程?
问题 3:除以上方法外,还能怎样列方程?
问题 4:配套问题的共同点是?
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
1、同时生产两种不同的东西;
3、两种东西在数量上存在数量关系;以这种数量关系找出相等关系,建立方程。
2、工人、器械或者原料数量一定;
动动脑,动动手。
练习一:某服装厂加工车间有54人,每人每天可以加工上衣8件或裤子10条。应怎样分配人数,才能使每天生产的上衣和裤子配套?(一件上衣与一条裤子为一套)
练习二:在加固某段河坝时,需要动用15台挖土、运土机械,每台机械每小时能挖土18立方米或运土12立方米,为了使挖出的土能及时运走,如何安排机械?
动动脑,动动手。
练习三:一张方桌由1个桌面、4个桌腿组成,如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好能配成方桌?
自学课本100页例2,完成以下问题,(用时5分钟)
问题 1:工作量、工作效率、工作时间之间存在什么样的数量关系?
问题 2:一般把工作量看做什么?
问题 3:填写下列表格?
问题 4:如何列方程?列方程解决实际问题的的基本过程是什么?一般步骤是什么?
自学指导1
人均效率 人数 时间 工作量
前一部分工作 4
后一部分工作 8
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:经常在题目中未给出工作总量时,设工作总量为单位1。
工程问题中的三个量及其关系为:
工作量=工作效率×工作时间
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:经常在题目中未给出工作总量时,设工作总量为单位1。
工程问题中的三个量及其关系为:
工作量=工作效率×工作时间
x
x+2
人均效率 人数 时间 工作量
前一部分工作 4
后一部分工作 8
解:设X人先做,依题意得:
4x+8(x+2)=40
4x+8x+16=40
12x=24
答:应先安排 2人做4 h.
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
一元一次方程的解
(x = a)
实际问题的答案
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
a1、某工程由甲、乙两队完成,甲队单独完成需16天,乙队单独完成需12天。如先由甲队做4天,然后两队合做,问再做几天后可完成工程?
2、一项工作甲工程队单独施工需要30天才能完成,乙队单独需要20天才能完成。现在由甲队单独工作5天之后,剩下的工作再由两队合作完成,问他们需要合作多少天?
3、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
分析:工作总量=工作效率×工作时间 。
两个队用的时间相同吗?
甲队的工作量+乙队的工作量=1
解:设 x多少天可以铺好这条管线.
当堂检测
1.课本101页练习题
1.对自己说,你有什么收获?
作业和总结
2.对老师说,你还有什么困惑?
作业:
课本106页复习巩固第2.3.4.5题
总结:
先小组讨论,再举手发言
1、同时生产两种不同的东西;
3、两种东西在数量上存在数量关系;以这种数量关系找出相等关系,建立方程。
2、工人、器械或者原料数量一定;
归纳总结
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
一元一次方程的解
(x = a)
实际问题的答案
归纳总结
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
归纳总结
没有比你更聪明的,只有比你更努力的!
——人生下来都是一样的,没有谁一生下来就是天才,之所以别人比你优秀,因为他付出了更多的努力。
解读格言:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
义务教育教科书 数学 七年级 上册
3.4实际问题与一元一次方程
配套问题和工程问题
第1课时
1.会通过列方程解决“配套问题”和“工程问题”
2.掌握列方程解决实际问题的一般步骤
3.通过列方程解决实际问题的过程,体会建模思想
学习目标
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
复习导入
自学课本100页例1,完成以下问题,(用时5分钟)
问题 1:填写下列表格,找出存在的数量关系?
问题 2:若设x名工人生产螺钉,如何列方程?
问题 3:除以上方法外,还能怎样列方程?
问题 4:配套问题的共同点是?
自学指导1
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
列表分析:
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
22﹣x
2 000(22-x)
1 200 x
x
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x
解方程,得: 5(22-x)=6x
110-5x=6x
x=10
生产螺母有:22-x=12(人)
答:应安排10名工人生产螺钉,12名工人生产螺母.
问题3:以上问题还有其他的解决方法吗?
如果设生产螺母的有x人,那方程应该怎么列呢?用上面那个解题的思路来做一下吧!
解:设生产螺母的有x人,生产螺钉的人有(22-x)人,由题意得:
2000x=2×1200×(22-x)
x
22﹣x
2000x
1200(22-x)
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
自学课本100页例1,完成以下问题,(用时5分钟)
问题 1:填写下列表格,找出存在的数量关系?
问题 2:若设x名工人生产螺钉,如何列方程?
问题 3:除以上方法外,还能怎样列方程?
问题 4:配套问题的共同点是?
产品类型 生产人数 单人产量 总产量
螺钉 1 200
螺母 2 000
1、同时生产两种不同的东西;
3、两种东西在数量上存在数量关系;以这种数量关系找出相等关系,建立方程。
2、工人、器械或者原料数量一定;
动动脑,动动手。
练习一:某服装厂加工车间有54人,每人每天可以加工上衣8件或裤子10条。应怎样分配人数,才能使每天生产的上衣和裤子配套?(一件上衣与一条裤子为一套)
练习二:在加固某段河坝时,需要动用15台挖土、运土机械,每台机械每小时能挖土18立方米或运土12立方米,为了使挖出的土能及时运走,如何安排机械?
动动脑,动动手。
练习三:一张方桌由1个桌面、4个桌腿组成,如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好能配成方桌?
自学课本100页例2,完成以下问题,(用时5分钟)
问题 1:工作量、工作效率、工作时间之间存在什么样的数量关系?
问题 2:一般把工作量看做什么?
问题 3:填写下列表格?
问题 4:如何列方程?列方程解决实际问题的的基本过程是什么?一般步骤是什么?
自学指导1
人均效率 人数 时间 工作量
前一部分工作 4
后一部分工作 8
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:经常在题目中未给出工作总量时,设工作总量为单位1。
工程问题中的三个量及其关系为:
工作量=工作效率×工作时间
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:经常在题目中未给出工作总量时,设工作总量为单位1。
工程问题中的三个量及其关系为:
工作量=工作效率×工作时间
x
x+2
人均效率 人数 时间 工作量
前一部分工作 4
后一部分工作 8
解:设X人先做,依题意得:
4x+8(x+2)=40
4x+8x+16=40
12x=24
答:应先安排 2人做4 h.
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
一元一次方程的解
(x = a)
实际问题的答案
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
a1、某工程由甲、乙两队完成,甲队单独完成需16天,乙队单独完成需12天。如先由甲队做4天,然后两队合做,问再做几天后可完成工程?
2、一项工作甲工程队单独施工需要30天才能完成,乙队单独需要20天才能完成。现在由甲队单独工作5天之后,剩下的工作再由两队合作完成,问他们需要合作多少天?
3、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
分析:工作总量=工作效率×工作时间 。
两个队用的时间相同吗?
甲队的工作量+乙队的工作量=1
解:设 x多少天可以铺好这条管线.
当堂检测
1.课本101页练习题
1.对自己说,你有什么收获?
作业和总结
2.对老师说,你还有什么困惑?
作业:
课本106页复习巩固第2.3.4.5题
总结:
先小组讨论,再举手发言
1、同时生产两种不同的东西;
3、两种东西在数量上存在数量关系;以这种数量关系找出相等关系,建立方程。
2、工人、器械或者原料数量一定;
归纳总结
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
一元一次方程的解
(x = a)
实际问题的答案
归纳总结
1. 审:审题,分析题目中的数量关系;
2. 设:设未知数,可直接设也可间接设;
3. 列:根据题目中的数量相等关系列方程;
4. 解:解这个方程;
5. 检:检验所求的解是否符合题意.
列方程解应用问题的一般步骤是?
6. 答:写出答案(有单位的要在答案中注明).
归纳总结
没有比你更聪明的,只有比你更努力的!
——人生下来都是一样的,没有谁一生下来就是天才,之所以别人比你优秀,因为他付出了更多的努力。
解读格言:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
