北师大版数学必修4同步教学课:第2章-3.1 数乘向量
文档属性
| 名称 | 北师大版数学必修4同步教学课:第2章-3.1 数乘向量 |

|
|
| 格式 | zip | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览








文档简介
课件29张PPT。§3 从速度的倍数到数乘向量
3.1 数乘向量
内容要求 1.掌握向量数乘的运算及其运算律(重点).2.理解数乘向量的几何意义(重点).3.掌握向量共线的判定定理和性质定理(难点).
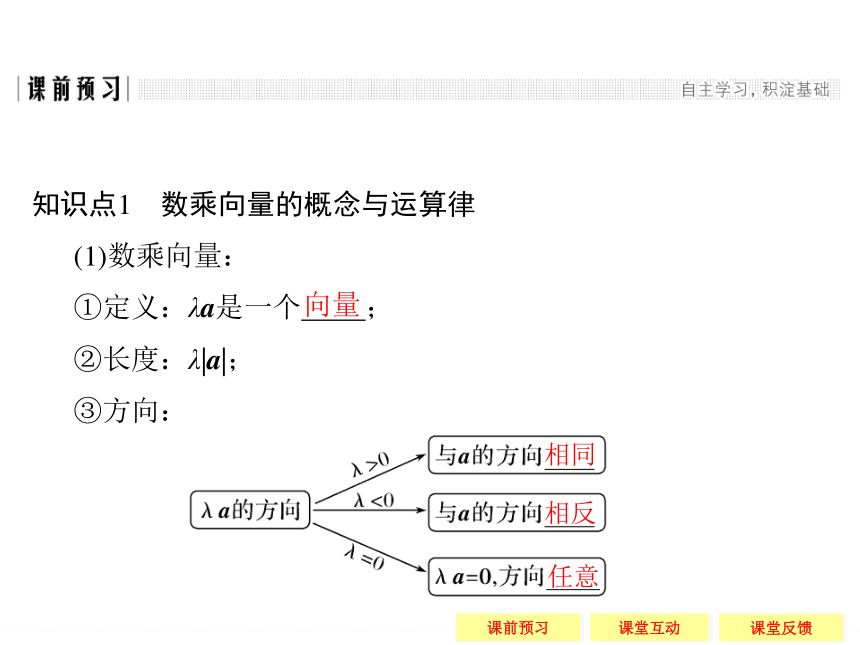
知识点1 数乘向量的概念与运算律
(1)数乘向量:
①定义:λa是一个 ;
②长度:λ|a|;
③方向:向量 相同 相反 任意 (2)数乘向量的运算律:
①λ(μa)= (λ,μ∈R);
②(λ+μ)a= (λ,μ∈R);
③λ(a+b)= (λ∈R).(λμ)a λa+μa λa+λb ××√知识点2 向量共线的判定定理与性质定理
(1)判定定理:a是一个非零向量,若存在一个实数λ,使得b=λa,则向量b与非零向量a共线.
(2)性质定理:若向量b与非零向量a共线,则存在一个实数λ,使得b=λa.【预习评价】
1.若a∥b,b∥c,那么一定有a∥c吗?
提示 不一定,若b=0,此时必有a∥b,b∥c成立,但a与c不一定共线.
2.如果向量a,b共线,一定有b=λa(λ∈R)吗?
提示 不一定.当a=0,b≠0时,λ不存在.规律方法 对数乘向量的四点说明
(1)λa的实数λ叫作向量a的系数.
(2)向量数乘运算的几何意义是把a沿着a的方向或a的反方向扩大或缩小.
(3)当λ=0或a=0时,λa=0.注意是0,而不是0.
(4)向量的运算不满足消去律,不能除以一个向量.【训练1】 已知λ,μ∈R,则在下列各命题中,正确的命题有( )
①λ<0,a≠0时,λa与a的方向一定相反;
②λ>0,a≠ 0时,λa与a的方向一定相同;
③λμ>0,a≠ 0时,λa与μa的方向一定相同;
④λμ<0,a≠ 0时,λa与μa的方向一定相反.
A.1个 B.2个
C.3个 D.4个解析 由λ与向量a的积λa的方向规定,易知①②正确,对于命题③④,当λμ>0时,λ,μ同正或同负,∴λa与μa或者都与a同向,或者都与a反向,∴λa与μa同向,当λμ<0时,则λ与μ异号,λa与μa中,一个与a同向,一个与a反向,∴λa与μa反向,故③④也正确.
答案 D规律方法 向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取公因式”,但这里的“同类项”“公因式”指向量,实数看作是向量的系数.【训练2】 若a=b+c,化简3(a+2b)-2(3b+c)-2(a+b)的结果为( )
A.-a B.-4b
C.c D.a-b
解析 3(a+2b)-2(3b+c)-2(a+b)=(3-2)a+(6-6-2) b-2 c =a-2(b+ c)=a-2a=-a.
答案 A规律方法 应用向量共线定理时的注意点
(1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.
(2)向量a,b共线是指存在不全为零的实数λ1,λ2,使λ1a+λ2b=0成立,若λ1a+λ2b=0,当且仅当λ1=λ2=0时成立,则向量a,b不共线. 解析 向量的数乘运算结果仍为向量,显然只有|3a|不是向量.
答案 C 答案 C 答案 2 答案 -3
3.1 数乘向量
内容要求 1.掌握向量数乘的运算及其运算律(重点).2.理解数乘向量的几何意义(重点).3.掌握向量共线的判定定理和性质定理(难点).
知识点1 数乘向量的概念与运算律
(1)数乘向量:
①定义:λa是一个 ;
②长度:λ|a|;
③方向:向量 相同 相反 任意 (2)数乘向量的运算律:
①λ(μa)= (λ,μ∈R);
②(λ+μ)a= (λ,μ∈R);
③λ(a+b)= (λ∈R).(λμ)a λa+μa λa+λb ××√知识点2 向量共线的判定定理与性质定理
(1)判定定理:a是一个非零向量,若存在一个实数λ,使得b=λa,则向量b与非零向量a共线.
(2)性质定理:若向量b与非零向量a共线,则存在一个实数λ,使得b=λa.【预习评价】
1.若a∥b,b∥c,那么一定有a∥c吗?
提示 不一定,若b=0,此时必有a∥b,b∥c成立,但a与c不一定共线.
2.如果向量a,b共线,一定有b=λa(λ∈R)吗?
提示 不一定.当a=0,b≠0时,λ不存在.规律方法 对数乘向量的四点说明
(1)λa的实数λ叫作向量a的系数.
(2)向量数乘运算的几何意义是把a沿着a的方向或a的反方向扩大或缩小.
(3)当λ=0或a=0时,λa=0.注意是0,而不是0.
(4)向量的运算不满足消去律,不能除以一个向量.【训练1】 已知λ,μ∈R,则在下列各命题中,正确的命题有( )
①λ<0,a≠0时,λa与a的方向一定相反;
②λ>0,a≠ 0时,λa与a的方向一定相同;
③λμ>0,a≠ 0时,λa与μa的方向一定相同;
④λμ<0,a≠ 0时,λa与μa的方向一定相反.
A.1个 B.2个
C.3个 D.4个解析 由λ与向量a的积λa的方向规定,易知①②正确,对于命题③④,当λμ>0时,λ,μ同正或同负,∴λa与μa或者都与a同向,或者都与a反向,∴λa与μa同向,当λμ<0时,则λ与μ异号,λa与μa中,一个与a同向,一个与a反向,∴λa与μa反向,故③④也正确.
答案 D规律方法 向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取公因式”,但这里的“同类项”“公因式”指向量,实数看作是向量的系数.【训练2】 若a=b+c,化简3(a+2b)-2(3b+c)-2(a+b)的结果为( )
A.-a B.-4b
C.c D.a-b
解析 3(a+2b)-2(3b+c)-2(a+b)=(3-2)a+(6-6-2) b-2 c =a-2(b+ c)=a-2a=-a.
答案 A规律方法 应用向量共线定理时的注意点
(1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.
(2)向量a,b共线是指存在不全为零的实数λ1,λ2,使λ1a+λ2b=0成立,若λ1a+λ2b=0,当且仅当λ1=λ2=0时成立,则向量a,b不共线. 解析 向量的数乘运算结果仍为向量,显然只有|3a|不是向量.
答案 C 答案 C 答案 2 答案 -3
