北师大版数学必修4同步教学课:第2章-6 平面向量数量积的坐标表示
文档属性
| 名称 | 北师大版数学必修4同步教学课:第2章-6 平面向量数量积的坐标表示 |

|
|
| 格式 | zip | ||
| 文件大小 | 608.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览











文档简介
课件30张PPT。§6 平面向量数量积的坐标表示内容要求 1.掌握数量积的坐标表达式,会进行平面向量数量积的运算(重点).2.能运用向量数量积的坐标表达式表示两个向量的夹角,会判断两个向量的垂直关系(难点).
知识点1 平面向量的数量积、模、夹角、垂直的坐标表示
(1)数量积的坐标表示:
设向量a=(x1,y1),b=(x2,y2),则a·b= .
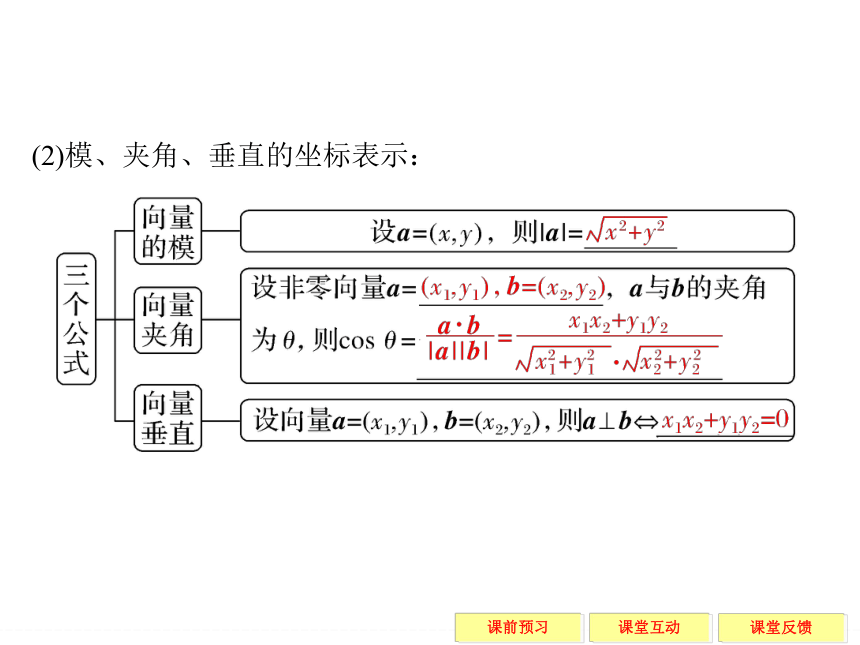
x1x2+y1y2 (2)模、夹角、垂直的坐标表示:
【预习评价】
1.已知向量a=(-4,7),向量b=(5,2),则a·b的值是( )
A.34 B.27
C.-43 D.-6
解析 a·b=(-4,7)·(5,2)=-4×5+7×2=-6.
答案 D 答案 C知识点2 直线的方向向量
(1)定义:与直线l 的非零向量m称为直线l的方向向量.
(2)性质:给定斜率为k的直线l的一个方向向量为m= .共线 (1,k) 【预习评价】
1.直线2x-3y+1=0的一个方向向量是( )
A.(2,-3) B.(2,3)
C.(-3,2) D.(3,2)
答案 D
2.过点A(-2,1)且与向量a=(3,1)平行的直线方程为_____.
答案 x-3y+5=0题型一 平面向量数量积的坐标运算
【例1】 已知向量a与b同向,b=(1,2),a·b=10,求:
(1)向量a的坐标;(2)若c=(2,-1),求(a·c)·b.规律方法 进行向量的数量积运算,前提是牢记有关的运算法则和运算性质.解题时通常有两条途径:一是先将各向量用坐标表示,直接进行数量积的坐标运算;二是先利用数量积的运算律将原式展开,再依据已知计算.【训练1】 已知向量a=(1,3),b=(2,5),c=(2,1).求:(1)a·b;(2)(a+b)·(2a-b);(3)(a·b)·c,a·(b·c).
解 (1)a·b=(1,3)·(2,5)=1×2+3×5=17.
(2)∵a+b=(1,3)+(2,5)=(3,8),
2a-b=2(1,3)-(2,5)=(2,6)-(2,5)=(0,1),
∴(a+b)·(2a-b)=(3,8)·(0,1)=3×0+8×1=8.
(3)(a·b)·c=17c=17(2,1)=(34,17),
a·(b·c)=a·[(2,5)·(2,1)]=(1,3)·(2×2+5×1)=9(1,3)=(9,27).规律方法 利用数量积求两向量夹角的步骤【训练2】 已知向量a=e1-e2,b=4e1+3e2,其中e1=(1,0),e2=(0,1).
(1)试计算a·b及|a+b|的值;
(2)求向量a与b夹角的余弦值.【例3】 设平面向量a=(1,1),b=(0,2).
求a-2b的坐标和模的大小.【迁移1】 若c=3a-(a·b)b,求|c|.【迁移2】 若ka-b与a+b共线,求k的值.
解 ∵a=(1,1),b=(0,-2),
ka-b=k(1,1)-(0,-2)=(k,k+2).
a+b=(1,1)+(0,-2)=(1,-1).
∵ka-b与a+b共线,
∴k+2-(-k)=0.∴k=-1.答案 B 答案 23.若a=(2,3),b=(-4,7),则a在b方向上的射影是________.4.已知平面向量a=(2,4),b=(-1,2),若c=a-(a·b)b,则|c|=________.5.已知a=(4,3),b=(-1,2).
(1)求a与b的夹角θ的余弦值;
(2)若(a-λb)⊥(2a+b),求实数λ的值.课堂小结
1.设a=(x1,y1),b=(x2,y2),则a⊥b?x1x2+y1y2=0.
应用该条件要注意:由a⊥b可得x1x2+y1y2=0;反过来,由x1x2+y1y2=0可得a⊥b.
2.向量的坐标表示与运算可以大大简化数量积的运算,由于有关长度、角度和垂直的问题可以利用向量的数量积来解决,因此可利用向量的坐标求出向量的长度、平面内两点间的距离、两个向量的夹角,可判断两向量是否垂直.
知识点1 平面向量的数量积、模、夹角、垂直的坐标表示
(1)数量积的坐标表示:
设向量a=(x1,y1),b=(x2,y2),则a·b= .
x1x2+y1y2 (2)模、夹角、垂直的坐标表示:
【预习评价】
1.已知向量a=(-4,7),向量b=(5,2),则a·b的值是( )
A.34 B.27
C.-43 D.-6
解析 a·b=(-4,7)·(5,2)=-4×5+7×2=-6.
答案 D 答案 C知识点2 直线的方向向量
(1)定义:与直线l 的非零向量m称为直线l的方向向量.
(2)性质:给定斜率为k的直线l的一个方向向量为m= .共线 (1,k) 【预习评价】
1.直线2x-3y+1=0的一个方向向量是( )
A.(2,-3) B.(2,3)
C.(-3,2) D.(3,2)
答案 D
2.过点A(-2,1)且与向量a=(3,1)平行的直线方程为_____.
答案 x-3y+5=0题型一 平面向量数量积的坐标运算
【例1】 已知向量a与b同向,b=(1,2),a·b=10,求:
(1)向量a的坐标;(2)若c=(2,-1),求(a·c)·b.规律方法 进行向量的数量积运算,前提是牢记有关的运算法则和运算性质.解题时通常有两条途径:一是先将各向量用坐标表示,直接进行数量积的坐标运算;二是先利用数量积的运算律将原式展开,再依据已知计算.【训练1】 已知向量a=(1,3),b=(2,5),c=(2,1).求:(1)a·b;(2)(a+b)·(2a-b);(3)(a·b)·c,a·(b·c).
解 (1)a·b=(1,3)·(2,5)=1×2+3×5=17.
(2)∵a+b=(1,3)+(2,5)=(3,8),
2a-b=2(1,3)-(2,5)=(2,6)-(2,5)=(0,1),
∴(a+b)·(2a-b)=(3,8)·(0,1)=3×0+8×1=8.
(3)(a·b)·c=17c=17(2,1)=(34,17),
a·(b·c)=a·[(2,5)·(2,1)]=(1,3)·(2×2+5×1)=9(1,3)=(9,27).规律方法 利用数量积求两向量夹角的步骤【训练2】 已知向量a=e1-e2,b=4e1+3e2,其中e1=(1,0),e2=(0,1).
(1)试计算a·b及|a+b|的值;
(2)求向量a与b夹角的余弦值.【例3】 设平面向量a=(1,1),b=(0,2).
求a-2b的坐标和模的大小.【迁移1】 若c=3a-(a·b)b,求|c|.【迁移2】 若ka-b与a+b共线,求k的值.
解 ∵a=(1,1),b=(0,-2),
ka-b=k(1,1)-(0,-2)=(k,k+2).
a+b=(1,1)+(0,-2)=(1,-1).
∵ka-b与a+b共线,
∴k+2-(-k)=0.∴k=-1.答案 B 答案 23.若a=(2,3),b=(-4,7),则a在b方向上的射影是________.4.已知平面向量a=(2,4),b=(-1,2),若c=a-(a·b)b,则|c|=________.5.已知a=(4,3),b=(-1,2).
(1)求a与b的夹角θ的余弦值;
(2)若(a-λb)⊥(2a+b),求实数λ的值.课堂小结
1.设a=(x1,y1),b=(x2,y2),则a⊥b?x1x2+y1y2=0.
应用该条件要注意:由a⊥b可得x1x2+y1y2=0;反过来,由x1x2+y1y2=0可得a⊥b.
2.向量的坐标表示与运算可以大大简化数量积的运算,由于有关长度、角度和垂直的问题可以利用向量的数量积来解决,因此可利用向量的坐标求出向量的长度、平面内两点间的距离、两个向量的夹角,可判断两向量是否垂直.
