北师大版数学必修4同步教学课:第2章-7 向量应用举例
文档属性
| 名称 | 北师大版数学必修4同步教学课:第2章-7 向量应用举例 |

|
|
| 格式 | zip | ||
| 文件大小 | 496.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览










文档简介
课件33张PPT。§7 向量应用举例 内容要求 1.能运用向量的有关知识解决解析几何中直线方程的问题,以及在平面几何中的线段平行、垂直、相等等问题(重点).2.能运用向量的有关知识解决物理中有关力、速度、功等问题(难点).
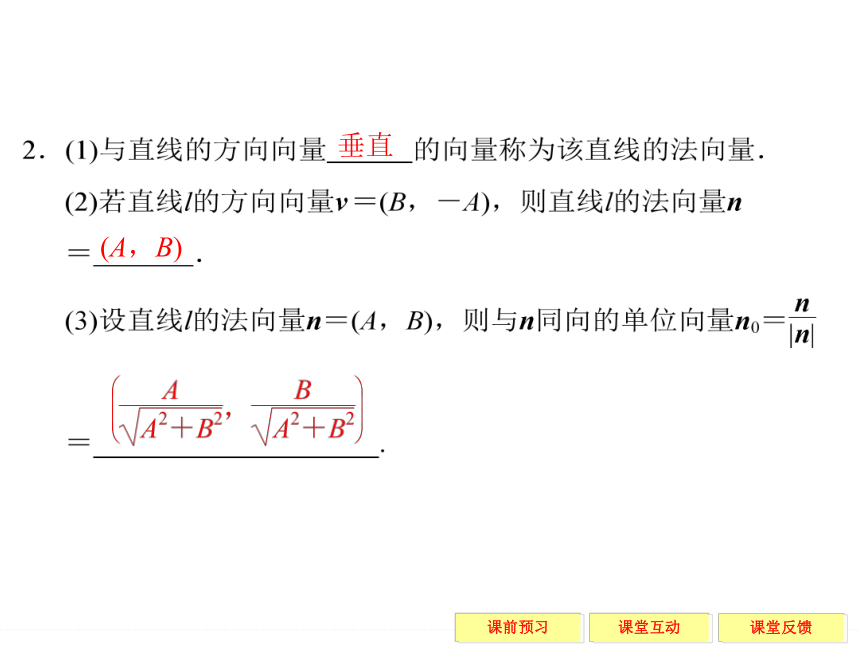
知识点1 点到直线的距离公式及直线的法向量
1.点M(x0,y0)到直线l:Ax+By+C=0的距离d= .垂直 (A,B) 【预习评价】
1.点P0(-1,2)到直线l:2x+y-10=0的距离为________.
2.直线2x-y+1=0的一个法向量是( )
A.(2,1) B.(-1,-2)
C.(1,2) D.(2,-1)
答案 D知识点2 向量的应用
向量的应用主要有两方面:一是在 中的应用;二是在 中的应用.几何 物理 答案 C2.已知F=(2,3)作用一物体,使物体从A(2,0)移动到B(4,0),则力F对物体作的功为________.
答案 4方向2 坐标法解决平面几何问题
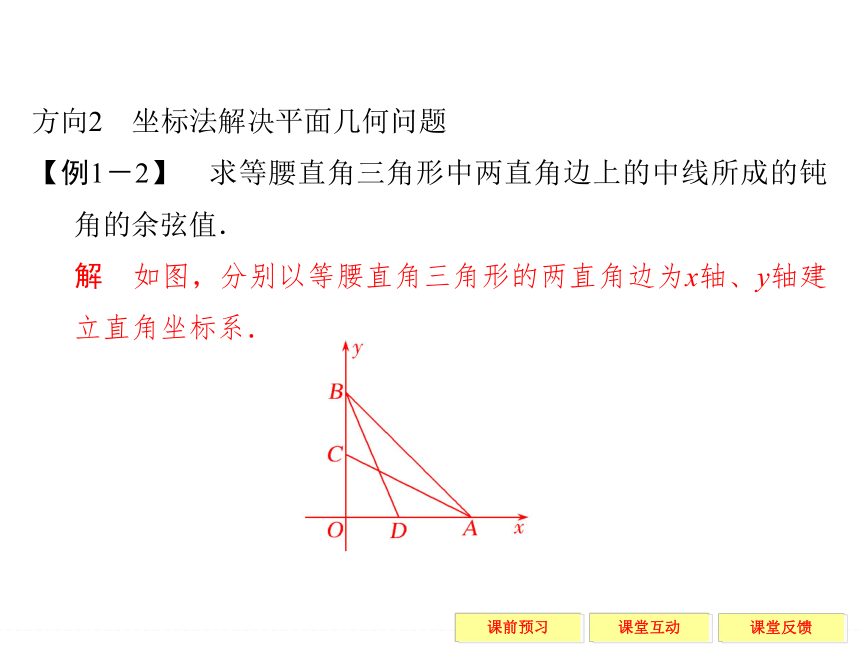
【例1-2】 求等腰直角三角形中两直角边上的中线所成的钝角的余弦值.
解 如图,分别以等腰直角三角形的两直角边为x轴、y轴建立直角坐标系.规律方法 用向量解平面几何问题的方法
(1)基底法(基向量法):选择两个不共线的向量作为基底,用基底表示有关向量,把问题转化为只含有基底向量的运算.
(2)坐标法:建立适当的坐标系,用坐标表示向量,把问题转化为向量的坐标运算.题型二 向量在解析几何中的应用
【例2】 已知直线l过点A(1,1),且它的一个法向量为n=(-2,1).
(1)求直线l的一般方程;
(2)若与直线l垂直的直线l1经过点B(2,0),求l1的一般方程.解 (1)∵直线l的一个法向量为n=(-2,1),
∴直线l的一个方向向量为v=(1,2).
∴直线l的斜率为2.
∴直线l的点斜式方程为y-1=2(x-1).
整理得2x-y-1=0.
故直线l的一般方程为2x-y-1=0.【训练1】
如图,在?OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若=x,=y(0(1)求y=f(x)的解析式;
(2)令F(x)=+x,判断F(x)的单调性,并给出你的证明.
规律方法 1.用向量解决物理问题首先要建立数学模型,把物理问题转化为数学问题,其次要注意物理中的矢量与数学中向量的区别与联系.
2.速度、加速度、位移、力的合成和分解,实质上就是向量的加减法运算,求解时常用向量求和的平行四边形法则和三角形法则.
3.在数学中,向量数量积的运算是由物理中力对物体所做的功抽象出来的,这也是向量在物理中的主要应用之一.【训练2】 一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4米/秒,这时气象台报告实际风速为2米/秒.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三对相对速度,汽车对地的速度为v车地、风对车的速度为v风车、风对地的速度为v风地,风对地的速度可以看成车对地与风对车的速度的合速度,即v风地=v风车+v车地. 答案 A 答案 D3.已知A(1,2),B(-2,1),以AB为直径的圆的方程是_______.
答案 x2+y2+x-3y=0 答案 305.正方形OABC的边长为1,点D,E分别为AB,BC的中点,试求cos∠DOE的值.课堂小结
1.用向量方法解决几何问题的关键是将几何问题转化为向量问题.对具体的问题是选用向量几何法还是向量坐标法是解题的关键.
2.用向量解决物理问题需注意:
(1)用向量方法解决相关的物理问题,要将相关物理量用几何图形表示出来.
(2)要根据它的物理意义列出数学模型,将物理问题转化为数学问题求解.
(3)要将数学问题还原为物理问题.
知识点1 点到直线的距离公式及直线的法向量
1.点M(x0,y0)到直线l:Ax+By+C=0的距离d= .垂直 (A,B) 【预习评价】
1.点P0(-1,2)到直线l:2x+y-10=0的距离为________.
2.直线2x-y+1=0的一个法向量是( )
A.(2,1) B.(-1,-2)
C.(1,2) D.(2,-1)
答案 D知识点2 向量的应用
向量的应用主要有两方面:一是在 中的应用;二是在 中的应用.几何 物理 答案 C2.已知F=(2,3)作用一物体,使物体从A(2,0)移动到B(4,0),则力F对物体作的功为________.
答案 4方向2 坐标法解决平面几何问题
【例1-2】 求等腰直角三角形中两直角边上的中线所成的钝角的余弦值.
解 如图,分别以等腰直角三角形的两直角边为x轴、y轴建立直角坐标系.规律方法 用向量解平面几何问题的方法
(1)基底法(基向量法):选择两个不共线的向量作为基底,用基底表示有关向量,把问题转化为只含有基底向量的运算.
(2)坐标法:建立适当的坐标系,用坐标表示向量,把问题转化为向量的坐标运算.题型二 向量在解析几何中的应用
【例2】 已知直线l过点A(1,1),且它的一个法向量为n=(-2,1).
(1)求直线l的一般方程;
(2)若与直线l垂直的直线l1经过点B(2,0),求l1的一般方程.解 (1)∵直线l的一个法向量为n=(-2,1),
∴直线l的一个方向向量为v=(1,2).
∴直线l的斜率为2.
∴直线l的点斜式方程为y-1=2(x-1).
整理得2x-y-1=0.
故直线l的一般方程为2x-y-1=0.【训练1】
如图,在?OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若=x,=y(0
(2)令F(x)=+x,判断F(x)的单调性,并给出你的证明.
规律方法 1.用向量解决物理问题首先要建立数学模型,把物理问题转化为数学问题,其次要注意物理中的矢量与数学中向量的区别与联系.
2.速度、加速度、位移、力的合成和分解,实质上就是向量的加减法运算,求解时常用向量求和的平行四边形法则和三角形法则.
3.在数学中,向量数量积的运算是由物理中力对物体所做的功抽象出来的,这也是向量在物理中的主要应用之一.【训练2】 一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4米/秒,这时气象台报告实际风速为2米/秒.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三对相对速度,汽车对地的速度为v车地、风对车的速度为v风车、风对地的速度为v风地,风对地的速度可以看成车对地与风对车的速度的合速度,即v风地=v风车+v车地. 答案 A 答案 D3.已知A(1,2),B(-2,1),以AB为直径的圆的方程是_______.
答案 x2+y2+x-3y=0 答案 305.正方形OABC的边长为1,点D,E分别为AB,BC的中点,试求cos∠DOE的值.课堂小结
1.用向量方法解决几何问题的关键是将几何问题转化为向量问题.对具体的问题是选用向量几何法还是向量坐标法是解题的关键.
2.用向量解决物理问题需注意:
(1)用向量方法解决相关的物理问题,要将相关物理量用几何图形表示出来.
(2)要根据它的物理意义列出数学模型,将物理问题转化为数学问题求解.
(3)要将数学问题还原为物理问题.
