北师大版数学必修4同步教学课:第3章-2.1+2.2 两角差的余弦函数 两角和与差的正弦、余弦函数
文档属性
| 名称 | 北师大版数学必修4同步教学课:第3章-2.1+2.2 两角差的余弦函数 两角和与差的正弦、余弦函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览










文档简介
课件33张PPT。§2 两角和与差的三角函数
2.1 两角差的余弦函数
2.2 两角和与差的正弦、余弦函数内容要求 1.会用向量的数量积推导出两角差的余弦公式(重点).2.能利用两角差的余弦公式导出两角差的正弦公式.3.能利用两角差的余弦公式导出两角和的正弦、余弦公式,了解它们的内在联系(重点).4.能运用上述公式进行简单恒等变换(难点).
知识点1 两角和与差的余弦公式
Cα+β:cos(α+β)= . (3.3)
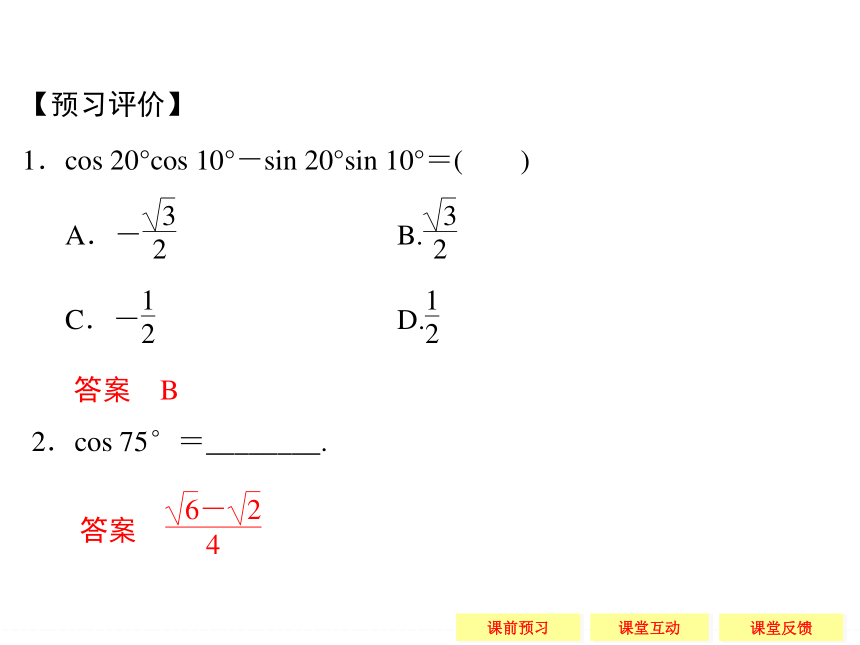
Cα-β:cos(α-β)= . (3.4)cos αcos β-sin αsin β cos αcos β+sin αsin β 答案 B
2.cos 75°=________.知识点2 两角和与差的正弦公式
Sα+β:sin(α+β)= . (3.5)
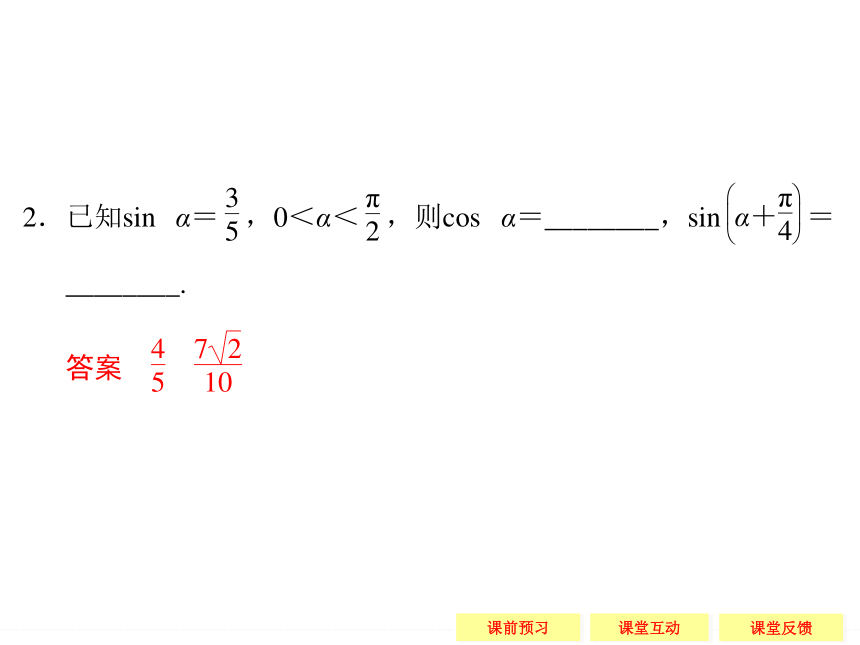
Sα-β:sin(α-β)= . (3.6)sin αcos β+cos αsin β sin αcos β-cos αsin β 答案 A题型一 给角求值
【例1】 求值:(1)sin 15°+cos 15°;
(2)sin 119°sin 181°-sin 91°sin 29°.规律方法 解此类题的关键是将非特殊角向特殊角转化,充分利用拆角、凑角的技巧转化为和、差角的正弦、余弦公式的形式,同时注意活用、逆用公式,“大角”利用诱导公式化为“小角”.【训练1】 求下列式子的值:
(1)cos(-15°);
(2)sin 795°;
(3)cos 43°cos 77°+sin 43°cos 167°.规律方法 在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角.具体做法是:
(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差.
(2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.答案 B 答案 B课堂小结
1.两角和与差的三角函数公式可以看成是诱导公式的推广,诱导公式可以看成两角和与差的三角函数公式的特例,例如:sin(π+α)=sin πcos α+cos πsin α=-sin α.2.使用和差公式时不仅要会正用,还要能够逆用公式,如化简sinβcos(α+β)-cos βsin(α+β)时,不要将cos(α+β)和sin(α+β)展开,而应采用整体思想,作如下变形:
sin βcos(α+β)-cos βsin(α+β)
=sin[β-(α+β)]=sin(-α)=-sin α.
3.运用和差公式求值、化简、证明时要注意灵活进行三角变换,有效地取得条件中的角与问题结论中的角之间的联系,选用恰当的公式快捷求解.
2.1 两角差的余弦函数
2.2 两角和与差的正弦、余弦函数内容要求 1.会用向量的数量积推导出两角差的余弦公式(重点).2.能利用两角差的余弦公式导出两角差的正弦公式.3.能利用两角差的余弦公式导出两角和的正弦、余弦公式,了解它们的内在联系(重点).4.能运用上述公式进行简单恒等变换(难点).
知识点1 两角和与差的余弦公式
Cα+β:cos(α+β)= . (3.3)
Cα-β:cos(α-β)= . (3.4)cos αcos β-sin αsin β cos αcos β+sin αsin β 答案 B
2.cos 75°=________.知识点2 两角和与差的正弦公式
Sα+β:sin(α+β)= . (3.5)
Sα-β:sin(α-β)= . (3.6)sin αcos β+cos αsin β sin αcos β-cos αsin β 答案 A题型一 给角求值
【例1】 求值:(1)sin 15°+cos 15°;
(2)sin 119°sin 181°-sin 91°sin 29°.规律方法 解此类题的关键是将非特殊角向特殊角转化,充分利用拆角、凑角的技巧转化为和、差角的正弦、余弦公式的形式,同时注意活用、逆用公式,“大角”利用诱导公式化为“小角”.【训练1】 求下列式子的值:
(1)cos(-15°);
(2)sin 795°;
(3)cos 43°cos 77°+sin 43°cos 167°.规律方法 在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角.具体做法是:
(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差.
(2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.答案 B 答案 B课堂小结
1.两角和与差的三角函数公式可以看成是诱导公式的推广,诱导公式可以看成两角和与差的三角函数公式的特例,例如:sin(π+α)=sin πcos α+cos πsin α=-sin α.2.使用和差公式时不仅要会正用,还要能够逆用公式,如化简sinβcos(α+β)-cos βsin(α+β)时,不要将cos(α+β)和sin(α+β)展开,而应采用整体思想,作如下变形:
sin βcos(α+β)-cos βsin(α+β)
=sin[β-(α+β)]=sin(-α)=-sin α.
3.运用和差公式求值、化简、证明时要注意灵活进行三角变换,有效地取得条件中的角与问题结论中的角之间的联系,选用恰当的公式快捷求解.
