北师大版数学必修4同步教学课:第3章-2.3 两角和与差的正切函数
文档属性
| 名称 | 北师大版数学必修4同步教学课:第3章-2.3 两角和与差的正切函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览











文档简介
课件30张PPT。2.3 两角和与差的正切函数 内容要求 能够利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式,并能灵活运用公式及变形解决相关问题(重、难点).
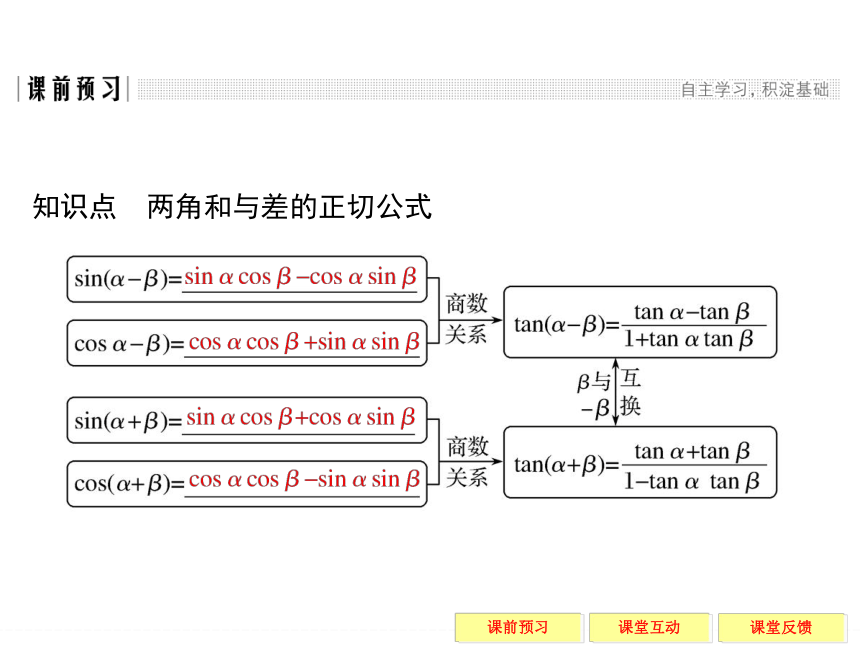
知识点 两角和与差的正切公式 答案 A【探究4】 已知A、B、C是三角形ABC的三个内角,且tan A、tan B是方程3x2+8x-1=0的两个实根,求tan C.规律方法 “给值求值”即给出某些角的三角函数的值,求另外一些角的三角函数值,解题的关键在于先用公式分析待求问题需要什么,然后利用化归的思想,把未知向已知转化.解题过程中须多加注意角的范围,必要时实行拆分角.规律方法 在求角问题中,常常出现忽视角的范围而出现增根不能排除的错误,因此在解答该类问题时,应尽量缩小角的范围,使得该范围内的角和所求得的函数值一一对应. 答案 A2.已知A+B=45°,则(1+tan A)(1+tan B)的值为( )
A.1 B.2
C.-2 D.不确定
解析 (1+tan A)(1+tan B)
=1+(tan A+tan B)+tan Atan B
=1+tan(A+B)(1-tan Atan B)+tan Atan B
=1+1-tan Atan B+tan Atan B=2.
答案 B5.若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.3.公式Tα±β的变形应用
只要见到tan α±tan β,tan αtan β时,要有灵活应用公式Tα±β的意识,就不难想到解题思路.
知识点 两角和与差的正切公式 答案 A【探究4】 已知A、B、C是三角形ABC的三个内角,且tan A、tan B是方程3x2+8x-1=0的两个实根,求tan C.规律方法 “给值求值”即给出某些角的三角函数的值,求另外一些角的三角函数值,解题的关键在于先用公式分析待求问题需要什么,然后利用化归的思想,把未知向已知转化.解题过程中须多加注意角的范围,必要时实行拆分角.规律方法 在求角问题中,常常出现忽视角的范围而出现增根不能排除的错误,因此在解答该类问题时,应尽量缩小角的范围,使得该范围内的角和所求得的函数值一一对应. 答案 A2.已知A+B=45°,则(1+tan A)(1+tan B)的值为( )
A.1 B.2
C.-2 D.不确定
解析 (1+tan A)(1+tan B)
=1+(tan A+tan B)+tan Atan B
=1+tan(A+B)(1-tan Atan B)+tan Atan B
=1+1-tan Atan B+tan Atan B=2.
答案 B5.若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.3.公式Tα±β的变形应用
只要见到tan α±tan β,tan αtan β时,要有灵活应用公式Tα±β的意识,就不难想到解题思路.
