1.1.2 弧度制:28张PPT
图片预览








文档简介
课件28张PPT。1.1.2 弧度制内容要求 1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换(重点).2.体会引入弧度制的必要性,建立角的集合与实数集的一一对应关系.3.掌握并能应用弧度制下的弧长公式和扇形面积公式(重、难点).知识点1 弧度制
1.度量角的两种制度度 弧度 半径长 rad 2.弧度数的计算
(1)正角:正角的弧度数是一个_______.
(2)负角:负角的弧度数是一个_______.
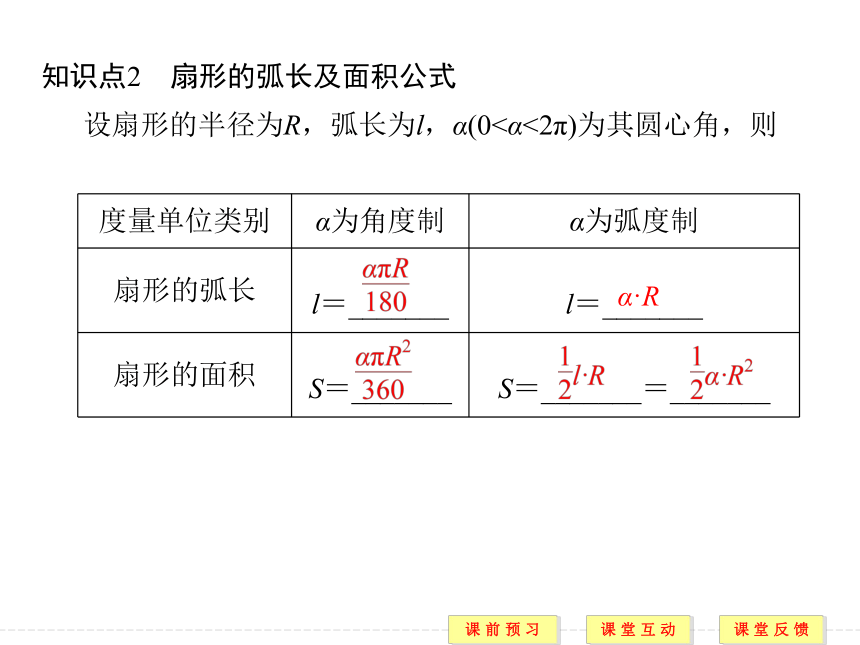
(3)零角:零角的弧度数是_______.正数 负数 0 3.角度制与弧度制的换算2π rad 360° π rad 180° 知识点2 扇形的弧长及面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则α·R 【预习评价】
圆的半径是6 cm,则圆心角为15°的扇形面积是________.题型一 角度与弧度的互化及应用【例2】 用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图).题型二 用弧度制表示角的集合
规律方法 根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.【例3】 已知一个扇形的周长为a,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.题型三 扇形的弧长公式及面积公式的应用【训练3】 已知扇形AOB的周长为10 cm.
(1)若这个扇形的面积为4 cm2,求扇形圆心角的弧度数;
(2)求该扇形的面积取得最大值时圆心角的大小及弧长. 解析 根据1度、1弧度的定义可知只有D为假命题,故选D.
答案 D课堂达标 答案 B 答案 C4.若θ=-5,则角θ的终边在( )
A.第四象限 B.第三象限
C.第二象限 D.第一象限 答案 D
5.已知α=1 690°.
(1)把α写成2kπ+β(k∈Z,β∈[0,2π))的形式;
(2)求θ,使θ与α终边相同,且θ∈(-4π,4π).1.角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
2.解答角度与弧度的互化问题的关键在于充分利用“180°=π rad”这一关系式.
3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.课堂小结
1.度量角的两种制度度 弧度 半径长 rad 2.弧度数的计算
(1)正角:正角的弧度数是一个_______.
(2)负角:负角的弧度数是一个_______.
(3)零角:零角的弧度数是_______.正数 负数 0 3.角度制与弧度制的换算2π rad 360° π rad 180° 知识点2 扇形的弧长及面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则α·R 【预习评价】
圆的半径是6 cm,则圆心角为15°的扇形面积是________.题型一 角度与弧度的互化及应用【例2】 用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图).题型二 用弧度制表示角的集合
规律方法 根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.【例3】 已知一个扇形的周长为a,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.题型三 扇形的弧长公式及面积公式的应用【训练3】 已知扇形AOB的周长为10 cm.
(1)若这个扇形的面积为4 cm2,求扇形圆心角的弧度数;
(2)求该扇形的面积取得最大值时圆心角的大小及弧长. 解析 根据1度、1弧度的定义可知只有D为假命题,故选D.
答案 D课堂达标 答案 B 答案 C4.若θ=-5,则角θ的终边在( )
A.第四象限 B.第三象限
C.第二象限 D.第一象限 答案 D
5.已知α=1 690°.
(1)把α写成2kπ+β(k∈Z,β∈[0,2π))的形式;
(2)求θ,使θ与α终边相同,且θ∈(-4π,4π).1.角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
2.解答角度与弧度的互化问题的关键在于充分利用“180°=π rad”这一关系式.
3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.课堂小结
