1.2.1 任意角的三角函数(二):27张PPT
文档属性
| 名称 | 1.2.1 任意角的三角函数(二):27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 20:41:05 | ||
图片预览






文档简介
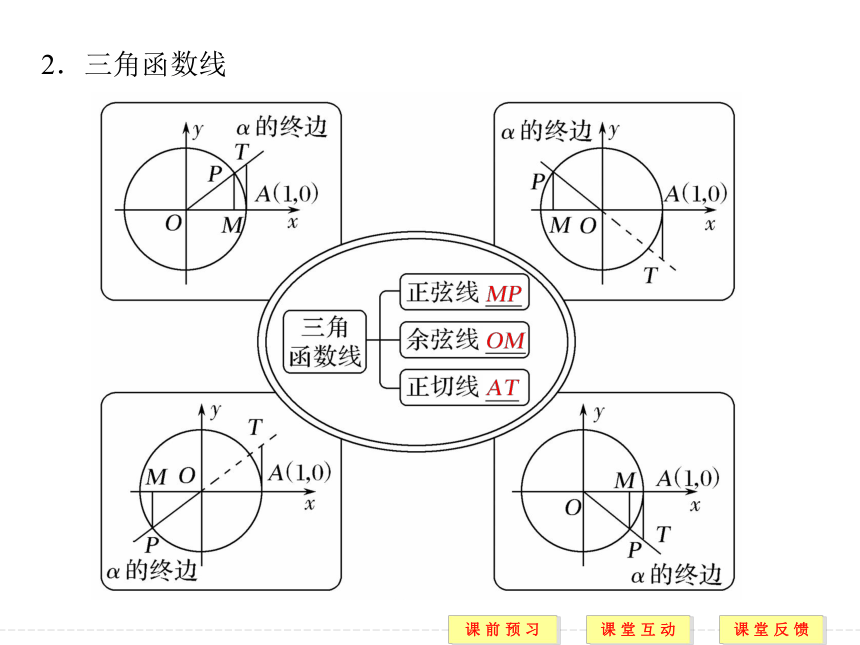
课件27张PPT。1.2.1 任意角的三角函数(二)内容要求 1.掌握正弦、余弦、正切函数的定义域(重点).2.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切(重点).3.能利用三角函数线解决一些简单的三角函数问题(难点).R R 知识点2 三角函数线
1.相关概念
(1)单位圆:
以原点O为圆心,以单位长度为半径的圆.
(2)有向线段:
带有_______ (规定了起点和终点)的线段.
规定:方向与x轴或y轴的正方向一致的为正值,反之为负值.
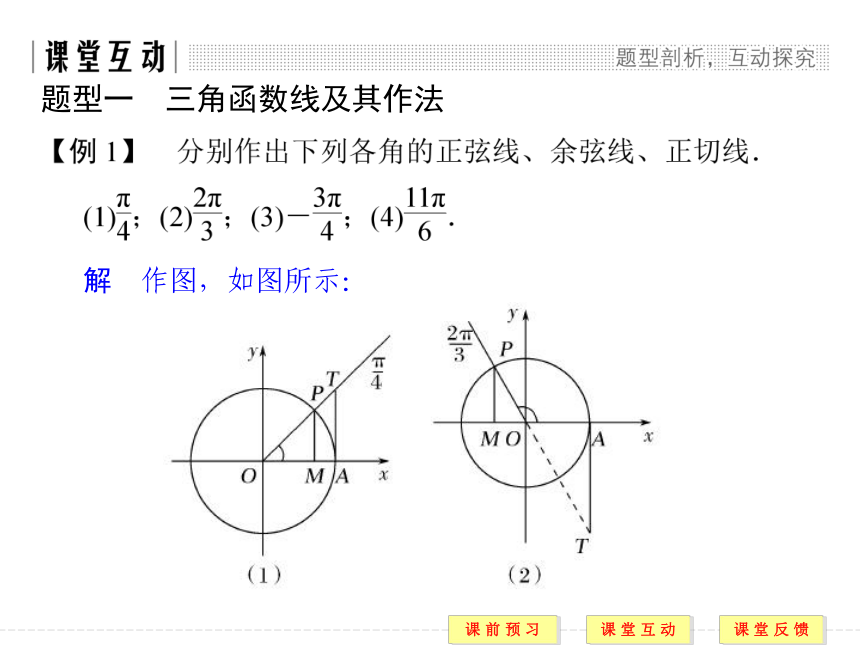
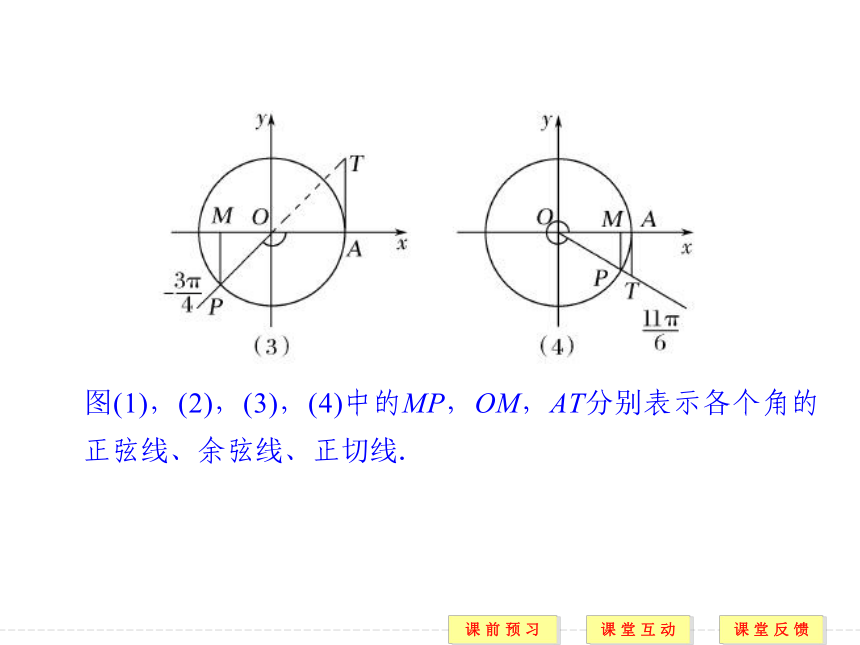
方向 2.三角函数线 解 作图,如图所示:题型一 三角函数线及其作法 图(1),(2),(3),(4)中的MP,OM,AT分别表示各个角的正弦线、余弦线、正切线. 规律方法 三角函数线的画法
(1)作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.
(2)作正切线时,应从A(1,0)点引x轴的垂线,交α的终边(α为第一或第四象限角)或α终边的反向延长线(α为第二或第三象限角)于点T,即可得到正切线AT.方向2 利用三角函数线解不等式
【例2-2】 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合: 规律方法 1.利用三角函数线比较大小的两个注意点
(1)角的终边的位置要找准;
(2)比较两个三角函数值的大小,不仅要看其长度,还要看其方向.
2.利用三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边范围.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,抓住边界值,然后再注意角的范围的写法要求. 规律方法 求三角函数定义域的方法
(1)求函数的定义域,就是求使解析式有意义的自变量的取值范围,一般通过解不等式或不等式组求得,对于三角函数的定义域问题,还要考虑三角函数自身定义域的限制.
(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时,可以用取特殊值把不固定的集合写成若干个固定集合再求交集.1.下列四个命题中:
①α一定时 ,单位圆中的正弦线一定;
②单位圆中,有相同正弦线的角相等;
③α和α+π有相同的正切线;
④具有相同正切线的两个角终边在同一条直线上.
不正确命题的个数是( )
A.0 B.1
C.2 D.3
解析 由三角函数线的定义①③④正确,②不正确.
答案 B课堂达标 方法二 如图所示,在单位圆中分别作出α的正弦线MP、余弦线OM、正切线AT,则OM sin α 答案 A 答案 <
1.相关概念
(1)单位圆:
以原点O为圆心,以单位长度为半径的圆.
(2)有向线段:
带有_______ (规定了起点和终点)的线段.
规定:方向与x轴或y轴的正方向一致的为正值,反之为负值.
方向 2.三角函数线 解 作图,如图所示:题型一 三角函数线及其作法 图(1),(2),(3),(4)中的MP,OM,AT分别表示各个角的正弦线、余弦线、正切线. 规律方法 三角函数线的画法
(1)作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.
(2)作正切线时,应从A(1,0)点引x轴的垂线,交α的终边(α为第一或第四象限角)或α终边的反向延长线(α为第二或第三象限角)于点T,即可得到正切线AT.方向2 利用三角函数线解不等式
【例2-2】 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合: 规律方法 1.利用三角函数线比较大小的两个注意点
(1)角的终边的位置要找准;
(2)比较两个三角函数值的大小,不仅要看其长度,还要看其方向.
2.利用三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边范围.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,抓住边界值,然后再注意角的范围的写法要求. 规律方法 求三角函数定义域的方法
(1)求函数的定义域,就是求使解析式有意义的自变量的取值范围,一般通过解不等式或不等式组求得,对于三角函数的定义域问题,还要考虑三角函数自身定义域的限制.
(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时,可以用取特殊值把不固定的集合写成若干个固定集合再求交集.1.下列四个命题中:
①α一定时 ,单位圆中的正弦线一定;
②单位圆中,有相同正弦线的角相等;
③α和α+π有相同的正切线;
④具有相同正切线的两个角终边在同一条直线上.
不正确命题的个数是( )
A.0 B.1
C.2 D.3
解析 由三角函数线的定义①③④正确,②不正确.
答案 B课堂达标 方法二 如图所示,在单位圆中分别作出α的正弦线MP、余弦线OM、正切线AT,则OM
