1.4.2 正弦函数、余弦函数的性质(二):30张PPT
文档属性
| 名称 | 1.4.2 正弦函数、余弦函数的性质(二):30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 20:47:36 | ||
图片预览










文档简介
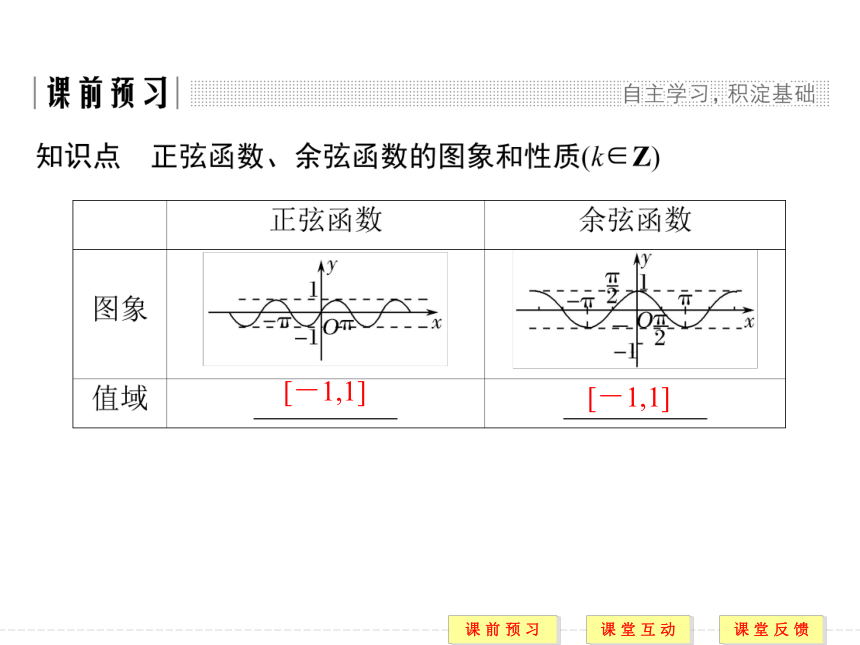
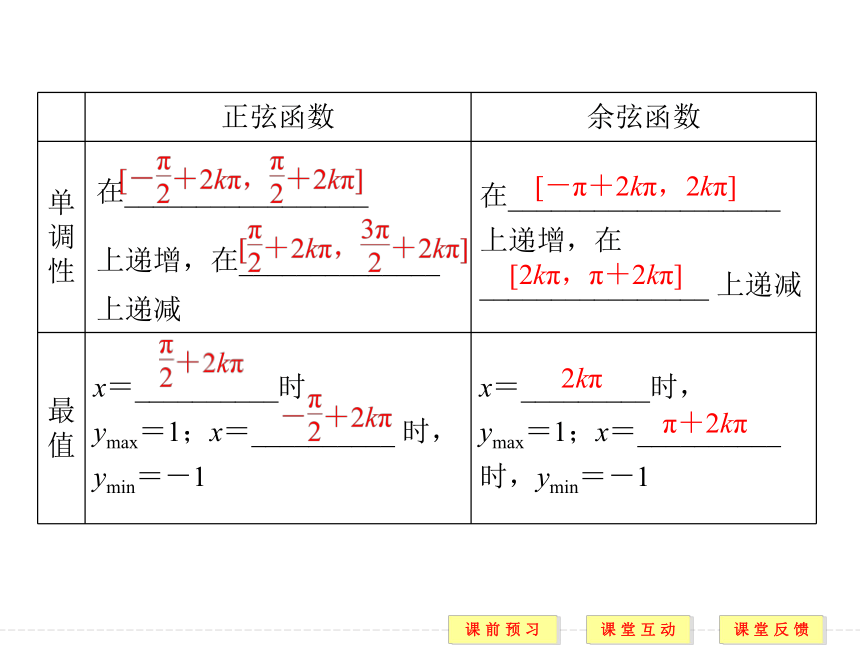
课件30张PPT。1.4.2 正弦函数、余弦函数的性质(二)内容要求 1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值(重点).2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小(重、难点).3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间(重点).[-1,1] [-1,1] [-π+2kπ,2kπ] [2kπ,π+2kπ] 2kπ π+2kπ 答案 C2.函数y=2-sin x取得最大值时x的值为________.题型一 正弦函数、余弦函数的单调性 答案 D
规律方法 单调区间的求法
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)的函数的单调区间,要先把ω化为正数,
(1)当A>0时,把ωx+φ整体放入y=sin x或y=cos x的单调增区间内,求得的x的范围即函数的增区间;放入y=sin x或y=cos x的单调减区间内,可求得函数的减区间.
(2)当A<0时,把ωx+φ整体放入y=sin x或y=cos x的单调增区间内,求得的x的范围即函数的减区间;放入y=sin x或y=cos x的单调减区间内,可求得函数的增区间.
提醒 求函数y=Asin(ωx+φ)的单调区间时,把ωx+φ看作一个整体,借助y=sin x的单调区间来解决.当A<0或ω<0时,要注意原函数的单调性与y=sin x的单调性的关系.题型二 利用正弦函数、余弦函数的单调性比较大小 规律方法 比较三角函数值的大小的步骤
(1)依据诱导公式把几个三角函数化为同名函数.
(2)依据诱导公式把角化到属于同一个单调增(减)区间.
(3)依据三角函数的单调性比较大小后写出结论. 规律方法 求三角函数值域或最值的常用方法
(1)可化为单一函数y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k,其最大值为|A|+k,最小值-|A|+k(其中A,ω,k,φ为常数,A≠0,ω≠0).
(2)可化为y=Asin2x+Bsin x+C或y=Acos2x+Bcos x+C (A≠0),最大值、最小值可利用二次函数在定义域上的最大值、最小值的求法来求(换元法).课堂达标 答案 A2.下列关系式中正确的是( )
A.sin 11° B.sin 168° C.sin 11° D.sin 168° 答案 C课堂小结2.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.
3.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
规律方法 单调区间的求法
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)的函数的单调区间,要先把ω化为正数,
(1)当A>0时,把ωx+φ整体放入y=sin x或y=cos x的单调增区间内,求得的x的范围即函数的增区间;放入y=sin x或y=cos x的单调减区间内,可求得函数的减区间.
(2)当A<0时,把ωx+φ整体放入y=sin x或y=cos x的单调增区间内,求得的x的范围即函数的减区间;放入y=sin x或y=cos x的单调减区间内,可求得函数的增区间.
提醒 求函数y=Asin(ωx+φ)的单调区间时,把ωx+φ看作一个整体,借助y=sin x的单调区间来解决.当A<0或ω<0时,要注意原函数的单调性与y=sin x的单调性的关系.题型二 利用正弦函数、余弦函数的单调性比较大小 规律方法 比较三角函数值的大小的步骤
(1)依据诱导公式把几个三角函数化为同名函数.
(2)依据诱导公式把角化到属于同一个单调增(减)区间.
(3)依据三角函数的单调性比较大小后写出结论. 规律方法 求三角函数值域或最值的常用方法
(1)可化为单一函数y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k,其最大值为|A|+k,最小值-|A|+k(其中A,ω,k,φ为常数,A≠0,ω≠0).
(2)可化为y=Asin2x+Bsin x+C或y=Acos2x+Bcos x+C (A≠0),最大值、最小值可利用二次函数在定义域上的最大值、最小值的求法来求(换元法).课堂达标 答案 A2.下列关系式中正确的是( )
A.sin 11°
3.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
