1.4.2 正弦函数、余弦函数的性质(一):31张PPT
文档属性
| 名称 | 1.4.2 正弦函数、余弦函数的性质(一):31张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 20:50:22 | ||
图片预览










文档简介
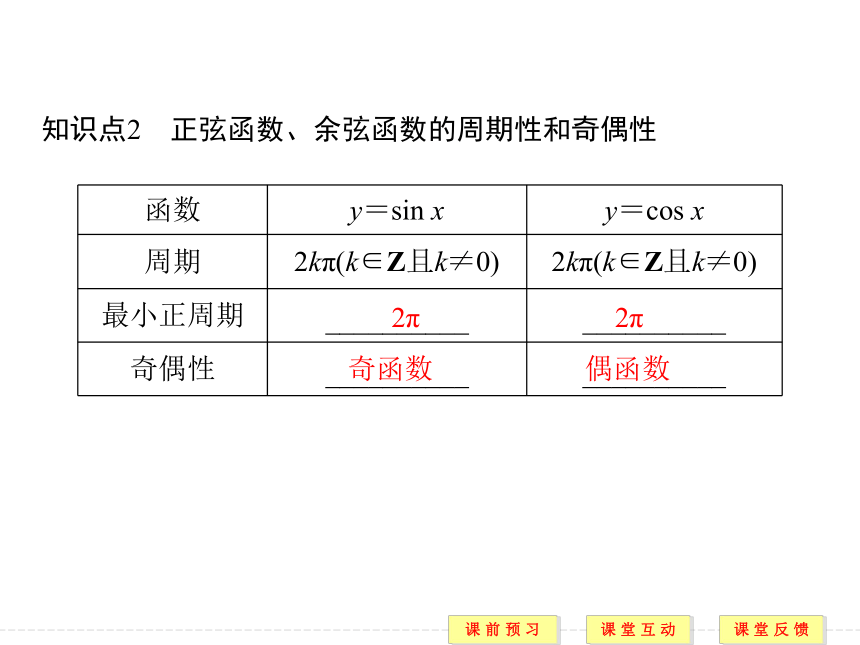
课件31张PPT。1.4.2 正弦函数、余弦函数的性质(一)内容要求 1.了解周期函数、周期、最小正周期的定义(重点).2.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的周期(重点).3.掌握函数y=sin x、y=cos x的奇偶性,会判断简单三角函数的奇偶性(重点).非零 f(x+T) 2.最小正周期正数 正数 【预习评价】 (正确的打“√”,错误的打“×”)
(1)周期函数y=f(x)的定义域可以为[a,b](a,b∈R).( )
(2)任何周期函数都有最小正周期.( )
(3)若存在正数T,使f(x+T)=-f(x),则函数f(x)的周期为2T.( )
提示 (1)×,周期函数的定义域一定为无限集,且无上下界.
(2)×,常数函数f(x)=c,任意一个正实数都是其周期,因而不存在最小正周期.
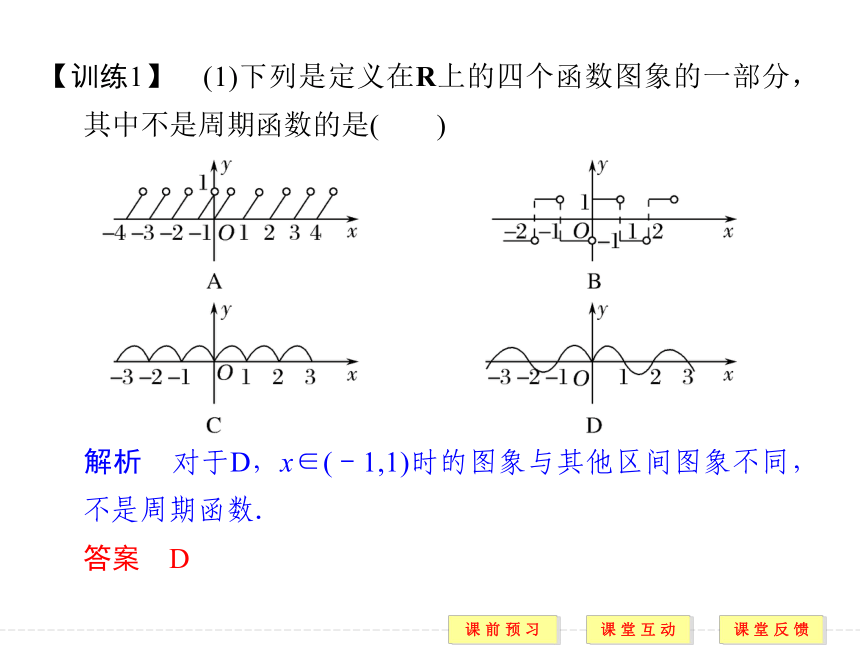
(3)√,f(x+2T)=f[(x+T)+T]=-f(x+T)=-[-f(x)]=f(x),所以f(x)的周期为2T.知识点2 正弦函数、余弦函数的周期性和奇偶性2π 2π 奇函数 偶函数 答案 D题型一 求三角函数的周期【训练1】 (1)下列是定义在R上的四个函数图象的一部分,其中不是周期函数的是( )
解析 对于D,x∈(-1,1)时的图象与其他区间图象不同,不是周期函数.
答案 D 答案 D 规律方法 判断函数奇偶性的两个关键点
关键点一:看函数的定义域是否关于原点对称;
关键点二:看f(-x)与f(x)的关系.
对于三角函数奇偶性的判断,有时可根据诱导公式先将函数式化简后再判断. 解 (1)函数的定义域为R,
又f(-x)=|sin(-x)|+cos(-x)=|sin x|+cos x=f(x),所以f(x)是偶函数.
(2)由1-cos x≥0且cos x-1≥0,得cos x=1,从而x=2kπ,k∈Z,此时f(x)=0,故该函数既是奇函数又是偶函数. 答案 D 答案 D【迁移1】 若将例3(2)题中的“偶函数”改为“奇函数”,其他条件不变,结果如何? 规律方法 三角函数周期性与奇偶性的解题策略
(1)探求三角函数的周期,常用方法是公式法,即将函数化为y=Asin(ωx+φ)或y=Acos(ωx+φ)的形式,再利用公式求解.
(2)判断函数y=Asin(ωx+φ)或y=Acos(ωx+φ)是否具备奇偶性,关键是看它能否通过诱导公式转化为y=Asin ωx(Aω≠0)或y=Acosωx(Aω≠0)其中的一个. 答案 1课堂达标 答案 C 答案 C 答案 ±π课堂小结2.判断函数的奇偶性,必须坚持“定义域优先”的原则,准确求函数定义域和将式子合理变形是解决此类问题的关键.如果定义域关于原点对称,再看f(-x)与f(x)的关系,从而判断奇偶性.
(1)周期函数y=f(x)的定义域可以为[a,b](a,b∈R).( )
(2)任何周期函数都有最小正周期.( )
(3)若存在正数T,使f(x+T)=-f(x),则函数f(x)的周期为2T.( )
提示 (1)×,周期函数的定义域一定为无限集,且无上下界.
(2)×,常数函数f(x)=c,任意一个正实数都是其周期,因而不存在最小正周期.
(3)√,f(x+2T)=f[(x+T)+T]=-f(x+T)=-[-f(x)]=f(x),所以f(x)的周期为2T.知识点2 正弦函数、余弦函数的周期性和奇偶性2π 2π 奇函数 偶函数 答案 D题型一 求三角函数的周期【训练1】 (1)下列是定义在R上的四个函数图象的一部分,其中不是周期函数的是( )
解析 对于D,x∈(-1,1)时的图象与其他区间图象不同,不是周期函数.
答案 D 答案 D 规律方法 判断函数奇偶性的两个关键点
关键点一:看函数的定义域是否关于原点对称;
关键点二:看f(-x)与f(x)的关系.
对于三角函数奇偶性的判断,有时可根据诱导公式先将函数式化简后再判断. 解 (1)函数的定义域为R,
又f(-x)=|sin(-x)|+cos(-x)=|sin x|+cos x=f(x),所以f(x)是偶函数.
(2)由1-cos x≥0且cos x-1≥0,得cos x=1,从而x=2kπ,k∈Z,此时f(x)=0,故该函数既是奇函数又是偶函数. 答案 D 答案 D【迁移1】 若将例3(2)题中的“偶函数”改为“奇函数”,其他条件不变,结果如何? 规律方法 三角函数周期性与奇偶性的解题策略
(1)探求三角函数的周期,常用方法是公式法,即将函数化为y=Asin(ωx+φ)或y=Acos(ωx+φ)的形式,再利用公式求解.
(2)判断函数y=Asin(ωx+φ)或y=Acos(ωx+φ)是否具备奇偶性,关键是看它能否通过诱导公式转化为y=Asin ωx(Aω≠0)或y=Acosωx(Aω≠0)其中的一个. 答案 1课堂达标 答案 C 答案 C 答案 ±π课堂小结2.判断函数的奇偶性,必须坚持“定义域优先”的原则,准确求函数定义域和将式子合理变形是解决此类问题的关键.如果定义域关于原点对称,再看f(-x)与f(x)的关系,从而判断奇偶性.
