1.4.3 正切函数的性质与图象:27张PPT
文档属性
| 名称 | 1.4.3 正切函数的性质与图象:27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 20:52:40 | ||
图片预览








文档简介
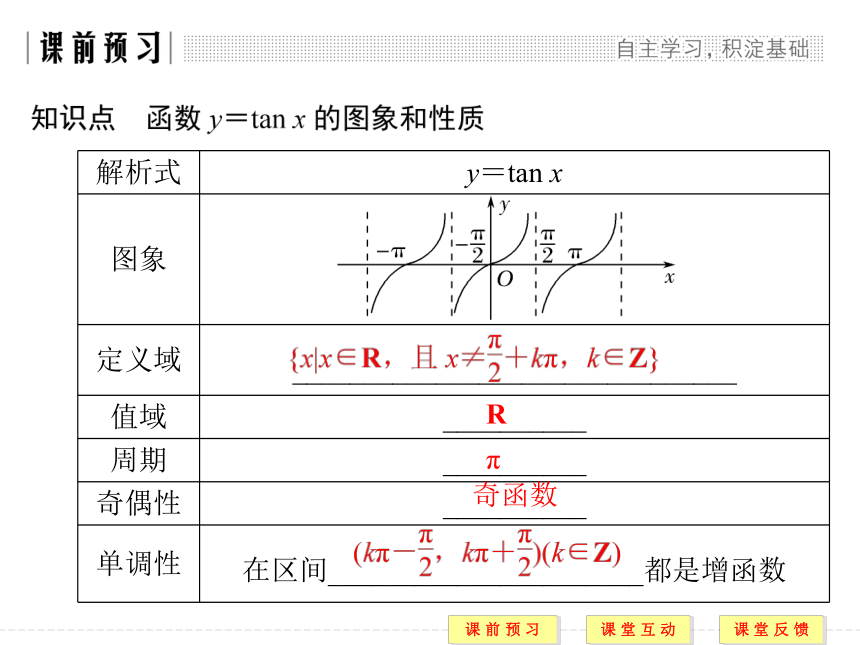
课件27张PPT。1.4.3 正切函数的性质与图象内容要求 1.了解正切函数图象的画法,理解并掌握正切函数的性质(重点).2.能利用正切函数的图象及性质解决有关问题(重点、难点). R π 奇函数 【预习评价】 (正确的打“√”,错误的打“×”)
(1)函数y=tan x在其定义域上是增函数.( )
(2)函数y=tan x的图象的对称中心是(kπ,0)(k∈Z).( )
(3)函数y=tan 2x的周期为π.( )题型一 正切函数的定义域、值域问题 答案 (-∞,1)
【训练1】 函数y=tan(sin x)的定义域为____________,值域为______________.
解析 因为-1≤sin x≤1,
所以tan(-1)≤tan(sin x)≤tan 1,
所以y=tan(sin x)的定义域为R,
值域为[-tan 1,tan 1].
答案 R [-tan 1,tan 1]【训练2】 比较tan 1,tan 2,tan 3的大小. 答案 C (2)画出函数y=|tan x|的图象,并根据图象判断其单调区间、奇偶性、周期性.
规律方法 1.作出函数y=|f(x)|的图象一般利用图象变换方法,具体步骤是:
(1)保留函数y=f(x)图象在x轴上方的部分;
(2)将函数y=f(x)图象在x轴下方的部分沿x轴向上翻折.
2.若函数为周期函数,可先研究其一个周期上的图象,再利用周期性,延拓到定义域上即可. 答案 A (2)画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.课堂达标 答案 C 答案 B 答案 > 答案 (-∞,-1]∪[1,+∞)5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.课堂小结
(1)函数y=tan x在其定义域上是增函数.( )
(2)函数y=tan x的图象的对称中心是(kπ,0)(k∈Z).( )
(3)函数y=tan 2x的周期为π.( )题型一 正切函数的定义域、值域问题 答案 (-∞,1)
【训练1】 函数y=tan(sin x)的定义域为____________,值域为______________.
解析 因为-1≤sin x≤1,
所以tan(-1)≤tan(sin x)≤tan 1,
所以y=tan(sin x)的定义域为R,
值域为[-tan 1,tan 1].
答案 R [-tan 1,tan 1]【训练2】 比较tan 1,tan 2,tan 3的大小. 答案 C (2)画出函数y=|tan x|的图象,并根据图象判断其单调区间、奇偶性、周期性.
规律方法 1.作出函数y=|f(x)|的图象一般利用图象变换方法,具体步骤是:
(1)保留函数y=f(x)图象在x轴上方的部分;
(2)将函数y=f(x)图象在x轴下方的部分沿x轴向上翻折.
2.若函数为周期函数,可先研究其一个周期上的图象,再利用周期性,延拓到定义域上即可. 答案 A (2)画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.课堂达标 答案 C 答案 B 答案 > 答案 (-∞,-1]∪[1,+∞)5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.课堂小结
