2.2.1 向量加法运算及其几何意义:30张PPT
文档属性
| 名称 | 2.2.1 向量加法运算及其几何意义:30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 21:11:38 | ||
图片预览






文档简介
课件30张PPT。§2.2 平面向量的线性运算
2.2.1 向量加法运算及其几何意义内容要求 1.理解并掌握向量加法的概念,了解向量加法的物理意义与几何意义.2.掌握向量加法的三角形法则和平行四边形法则,并能熟练运用这两个法则作两个向量的加法运算(重、难点).3.了解向量加法的交换律和结合律,并能依据几何意义作图解释向量加法运算律的合理性(难点).知识点1 向量的加法
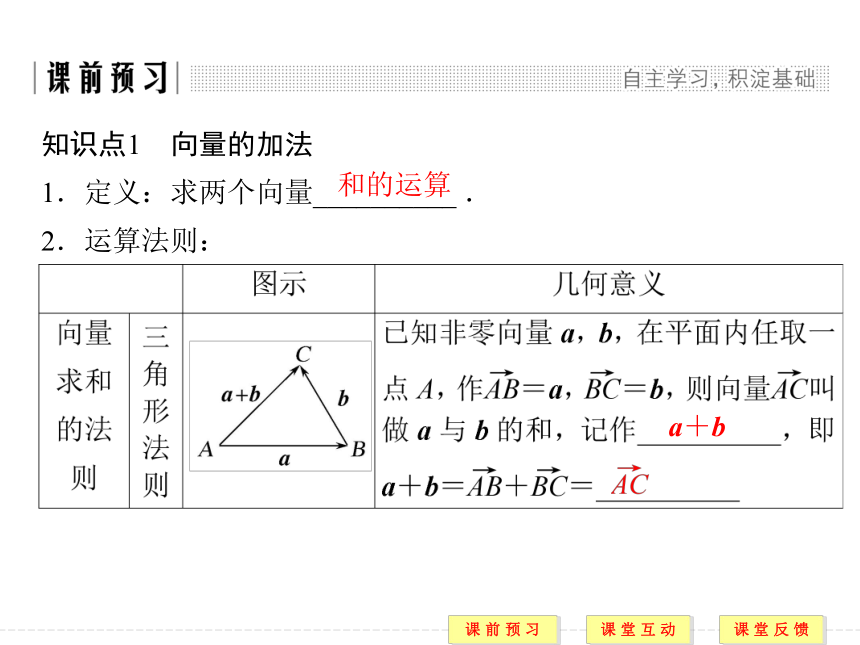
1.定义:求两个向量__________ .
2.运算法则:和的运算 a+b
【预习评价】
思考 三角形法则和平行四边形法则的使用条件有何不同?
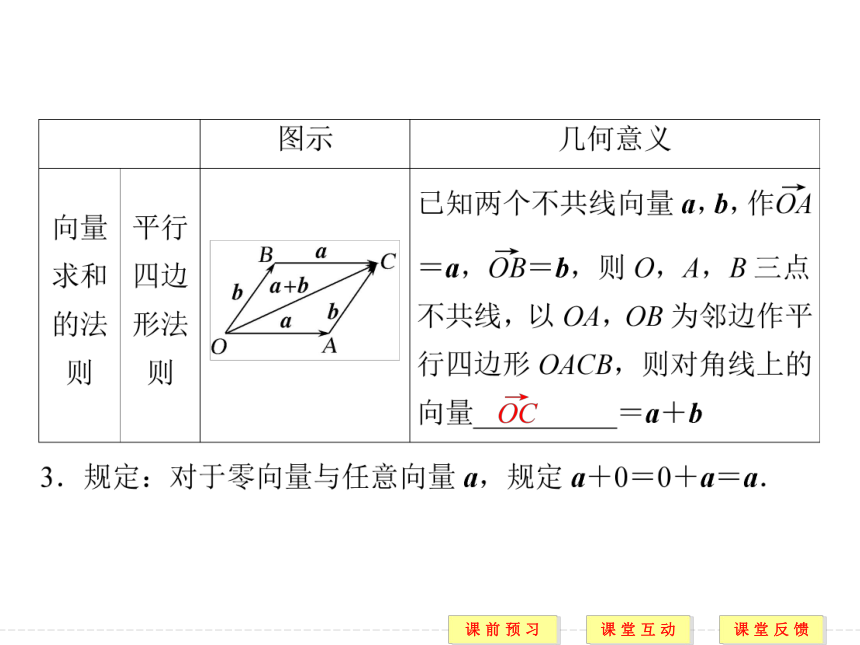
提示 三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.当两个向量不共线时,两个法则是一致的.知识点2 向量加法的运算律
1.交换律:a+b=b+a.
2.结合律:(a+b)+c=a+(b+c).
【预习评价】
已知非零向量a,b,c,则向量(a+c)+b,b+(a+c),b+(c+a),c+(b+a),c+(a+b)中,与向量a+b+c相等的个数为( )
A.2 B.3
C.4 D.5
解析 由向量加法的交换律与结合律可知,所给的5个向量都与a+b+c相等.
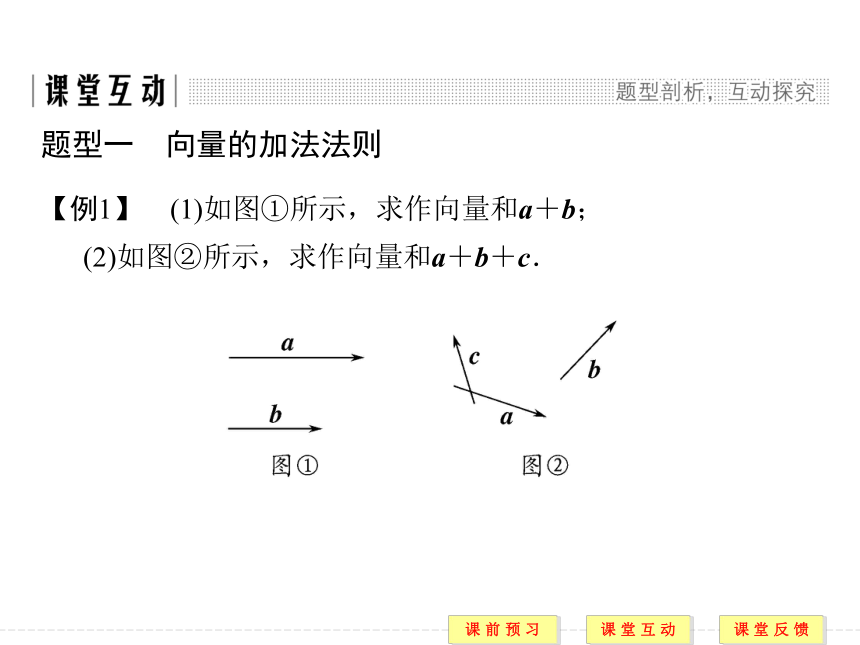
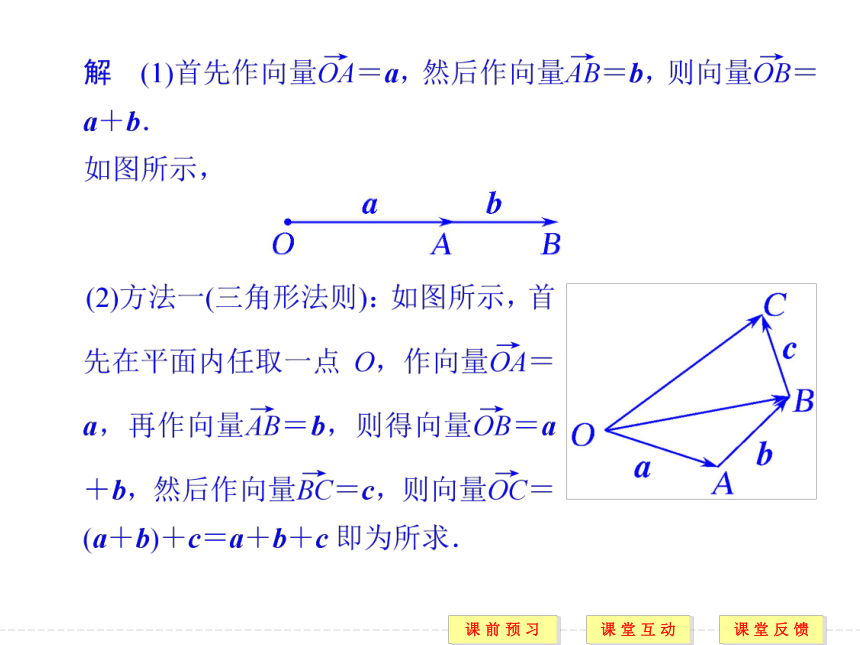
答案 D【例1】 (1)如图①所示,求作向量和a+b;
(2)如图②所示,求作向量和a+b+c.题型一 向量的加法法则 规律方法 向量求和的注意点
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和仍是一个向量.
(3)平行四边形法则对于两个向量共线时不适用.题型二 向量的加法及运算律 规律方法 向量加法运算律的意义和应用原则
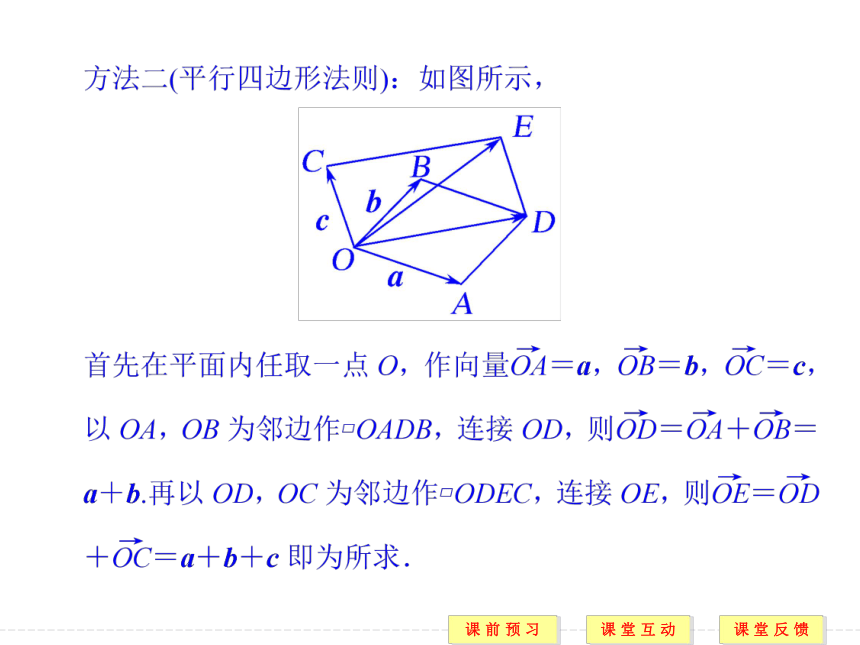
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.【例3】 在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
解 作出图形,如图.船速v船与岸的方向成α角,由图可知v水+v船=v实际,结合已知条件,四边形ABCD为平行四边形,【迁移1】 若例3条件不变,则经过3小时,该船的实际航程是多少km?【迁移2】 若例3的条件不变,改为若船沿垂直于水流的方向航行,求船实际行进的方向的正切值(相当于河岸的夹角). 规律方法 应用向量解决平面几何问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.【训练3】 如图所示,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.课堂达标 答案 C 答案 B 答案 D5.若a表示“向东走8 km”,b表示“向北走8 km”,求:
(1)|a+b|;(2)指出向量a+b的方向.1.三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是统一的.当两个向量首尾相连时常选用三角形法则,当两个向量共始点时,常选用平行四边形法则.
2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照任意的次序和任意的组合去进行.课堂小结
2.2.1 向量加法运算及其几何意义内容要求 1.理解并掌握向量加法的概念,了解向量加法的物理意义与几何意义.2.掌握向量加法的三角形法则和平行四边形法则,并能熟练运用这两个法则作两个向量的加法运算(重、难点).3.了解向量加法的交换律和结合律,并能依据几何意义作图解释向量加法运算律的合理性(难点).知识点1 向量的加法
1.定义:求两个向量__________ .
2.运算法则:和的运算 a+b
【预习评价】
思考 三角形法则和平行四边形法则的使用条件有何不同?
提示 三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.当两个向量不共线时,两个法则是一致的.知识点2 向量加法的运算律
1.交换律:a+b=b+a.
2.结合律:(a+b)+c=a+(b+c).
【预习评价】
已知非零向量a,b,c,则向量(a+c)+b,b+(a+c),b+(c+a),c+(b+a),c+(a+b)中,与向量a+b+c相等的个数为( )
A.2 B.3
C.4 D.5
解析 由向量加法的交换律与结合律可知,所给的5个向量都与a+b+c相等.
答案 D【例1】 (1)如图①所示,求作向量和a+b;
(2)如图②所示,求作向量和a+b+c.题型一 向量的加法法则 规律方法 向量求和的注意点
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和仍是一个向量.
(3)平行四边形法则对于两个向量共线时不适用.题型二 向量的加法及运算律 规律方法 向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.【例3】 在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
解 作出图形,如图.船速v船与岸的方向成α角,由图可知v水+v船=v实际,结合已知条件,四边形ABCD为平行四边形,【迁移1】 若例3条件不变,则经过3小时,该船的实际航程是多少km?【迁移2】 若例3的条件不变,改为若船沿垂直于水流的方向航行,求船实际行进的方向的正切值(相当于河岸的夹角). 规律方法 应用向量解决平面几何问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.【训练3】 如图所示,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.课堂达标 答案 C 答案 B 答案 D5.若a表示“向东走8 km”,b表示“向北走8 km”,求:
(1)|a+b|;(2)指出向量a+b的方向.1.三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是统一的.当两个向量首尾相连时常选用三角形法则,当两个向量共始点时,常选用平行四边形法则.
2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照任意的次序和任意的组合去进行.课堂小结
