2.2.2 向量减法运算及其几何意义:27张PPT
文档属性
| 名称 | 2.2.2 向量减法运算及其几何意义:27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 20:52:13 | ||
图片预览








文档简介
课件27张PPT。2.2.2 向量减法运算及其几何意义内容要求 1.理解相反向量的含义,向量减法的意义及减法法则(难点).2.掌握向量减法的几何意义(重点).3.能熟练地进行向量的加、减运算(重点).知识点1 相反向量相等 相反 知识点2 向量的减法
1.定义:a-b=__________.减去一个向量就等于加上这个向量的__________ .
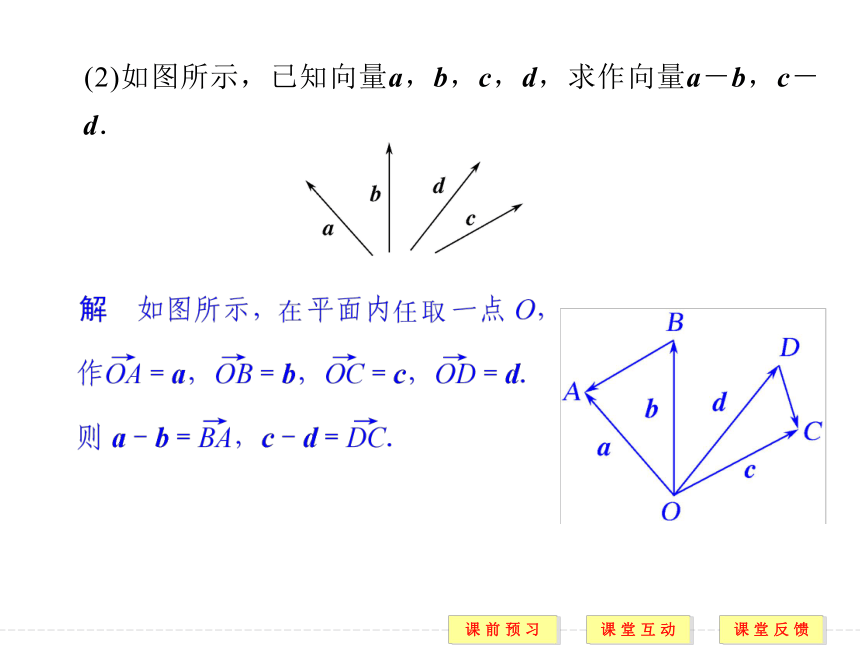
2.几何意义:a-b表示为从向量b的终点指向_____________ 的向量.a+(-b) 相反向量 向量a的终点 答案 C题型一 向量的减法 答案 B (2)如图所示,已知向量a,b,c,d,求作向量a-b,c-d.
规律方法 求作两个向量的差向量的两种思路
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
(2)可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量. 答案 ①④题型二 向量减法法则的运用 规律方法 1.向量减法运算的常用方法
2.向量加减法化简的两种形式
(1)首尾相连且为和.
(2)起点相同且为差.
解题时要注意观察是否有这两种形式,同时注意逆向应用.
题型三 向量减法的应用
规律方法 用向量表示其他向量的方法
(1)解决此类问题要充分利用平面几何知识,灵活运用平行四边形法则和三角形法则.
(2)表示向量时要考虑以下问题:它是某个平行四边形的对角线吗?是否可以找到由起点到终点的恰当途径?它的起点和终点是否是两个有共同起点的向量的终点?
(3)必要时可以直接用向量求和的多边形法则. 答案 D课堂达标 答案 B 答案 25.如图,已知a,b,求作a-b.
1.定义:a-b=__________.减去一个向量就等于加上这个向量的__________ .
2.几何意义:a-b表示为从向量b的终点指向_____________ 的向量.a+(-b) 相反向量 向量a的终点 答案 C题型一 向量的减法 答案 B (2)如图所示,已知向量a,b,c,d,求作向量a-b,c-d.
规律方法 求作两个向量的差向量的两种思路
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
(2)可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量. 答案 ①④题型二 向量减法法则的运用 规律方法 1.向量减法运算的常用方法
2.向量加减法化简的两种形式
(1)首尾相连且为和.
(2)起点相同且为差.
解题时要注意观察是否有这两种形式,同时注意逆向应用.
题型三 向量减法的应用
规律方法 用向量表示其他向量的方法
(1)解决此类问题要充分利用平面几何知识,灵活运用平行四边形法则和三角形法则.
(2)表示向量时要考虑以下问题:它是某个平行四边形的对角线吗?是否可以找到由起点到终点的恰当途径?它的起点和终点是否是两个有共同起点的向量的终点?
(3)必要时可以直接用向量求和的多边形法则. 答案 D课堂达标 答案 B 答案 25.如图,已知a,b,求作a-b.
