2.3.2、3 平面向量的正交分解及坐标表示 平面向量的坐标运算:28张PPT
文档属性
| 名称 | 2.3.2、3 平面向量的正交分解及坐标表示 平面向量的坐标运算:28张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 21:08:20 | ||
图片预览







文档简介
课件28张PPT。2.3.2 平面向量的正交分解及坐标表示2.3.3 平面向量的坐标运算内容要求 1.了解平面向量的正交分解,掌握向量的坐标表示(重点).2.掌握两个向量和、差及数乘向量的坐标运算法则(重点).3.正确理解向量坐标的概念,要把点的坐标与向量的坐标区分开来(易错点).知识点1 平面向量的坐标表示
1.平面向量的正交分解:把一个平面向量分解为两个__________ 的向量.
2.基底:在平面直角坐标系中,分别取与x轴、y轴方向相同的两个__________ i,j作为________ .互相垂直 单位向量 基底
3.坐标:对于平面内的一个向量a,有且仅有一对实数x,y,使得a=__________ ,则有序实数对(x,y)叫做向量a的坐标.
4.坐标表示:a=(x,y).
5.特殊向量的坐标:i=__________ ,j=__________ ,0=(0,0).
xi+yj (1,0) (0,1) 【预习评价】
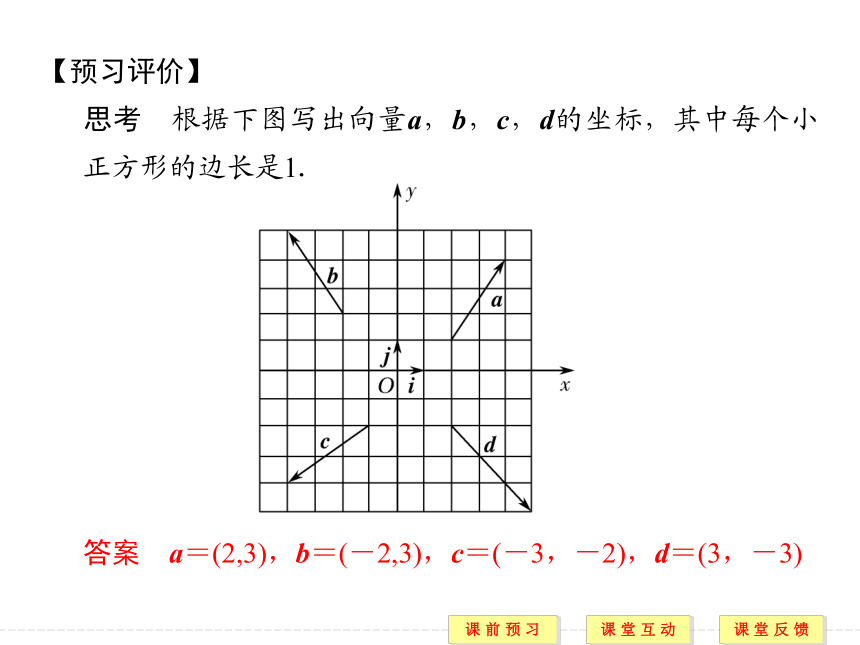
思考 根据下图写出向量a,b,c,d的坐标,其中每个小正方形的边长是1.
答案 a=(2,3),b=(-2,3),c=(-3,-2),d=(3,-3)知识点2 平面向量的坐标运算
设向量a=(x1,y1),b=(x2,y2),λ∈R,则有下表:和 (x1+x2,y1+y2) 差 (x1-x2,y1-y2) (λx,λy) 终点 起点
【预习评价】
已知向量a=(2,4),b=(-1,1),则2a-b=________.
解析 2a-b=2(2,4)-(-1,1)=(5,7).
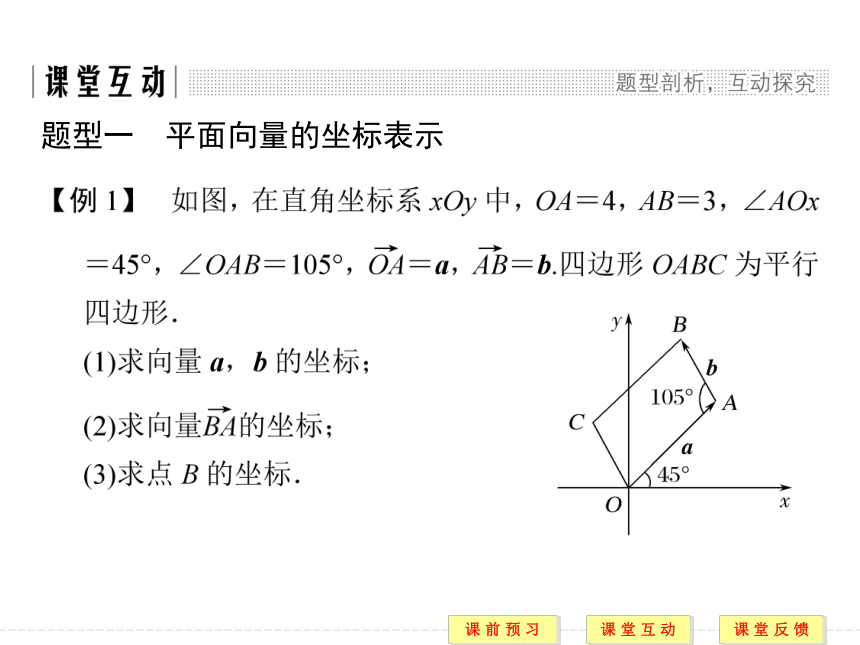
答案 (5,7)题型一 平面向量的坐标表示 规律方法 求点和向量坐标的常用方法
(1)求一个点的坐标,可以转化为求该点相对于坐标原点的位置的坐标.
(2)求一个向量的坐标时,可以首先求出这个向量的始点坐标和终点坐标,再运用终点坐标减去始点坐标得到该向量的坐标. 答案 A 答案 A 规律方法 平面向量坐标运算的技巧
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行.方向1 由相等的向量求参数的值
【例3-1】 已知向量a=(2,1),b=(1,-2),若ma+nb=(9,-8) (m,n∈R),则m-n的值为________.
答案 -3方向2 向量运算与平面几何的综合应用
【例3-2】已知平面上三点的坐标分别为A(-2,1),B(-1,3),C(3,4),求点D的坐标,使这四点构成平行四边形的四个顶点. 规律方法 坐标形式下向量相等的条件及其应用
(1)条件:相等向量的对应坐标相等.
(2)应用:利用坐标形式下向量相等的条件,可以建立相等关系,由此可以求出某些参数的值或点的坐标.课堂达标 答案 A 答案 A 答案 A 答案 (0,2)1.在平面直角坐标系中,平面内的点、以原点为起点的向量、有序实数对三者之间建立一一对应关系.关系图如图所示.课堂小结2.向量的坐标和这个向量的终点的坐标不一定相同.当且仅当向量的起点在原点时,向量的坐标才和这个终点的坐标相同.
3.向量坐标形式的计算,要牢记公式,细心计算,防止符号错误.
1.平面向量的正交分解:把一个平面向量分解为两个__________ 的向量.
2.基底:在平面直角坐标系中,分别取与x轴、y轴方向相同的两个__________ i,j作为________ .互相垂直 单位向量 基底
3.坐标:对于平面内的一个向量a,有且仅有一对实数x,y,使得a=__________ ,则有序实数对(x,y)叫做向量a的坐标.
4.坐标表示:a=(x,y).
5.特殊向量的坐标:i=__________ ,j=__________ ,0=(0,0).
xi+yj (1,0) (0,1) 【预习评价】
思考 根据下图写出向量a,b,c,d的坐标,其中每个小正方形的边长是1.
答案 a=(2,3),b=(-2,3),c=(-3,-2),d=(3,-3)知识点2 平面向量的坐标运算
设向量a=(x1,y1),b=(x2,y2),λ∈R,则有下表:和 (x1+x2,y1+y2) 差 (x1-x2,y1-y2) (λx,λy) 终点 起点
【预习评价】
已知向量a=(2,4),b=(-1,1),则2a-b=________.
解析 2a-b=2(2,4)-(-1,1)=(5,7).
答案 (5,7)题型一 平面向量的坐标表示 规律方法 求点和向量坐标的常用方法
(1)求一个点的坐标,可以转化为求该点相对于坐标原点的位置的坐标.
(2)求一个向量的坐标时,可以首先求出这个向量的始点坐标和终点坐标,再运用终点坐标减去始点坐标得到该向量的坐标. 答案 A 答案 A 规律方法 平面向量坐标运算的技巧
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行.方向1 由相等的向量求参数的值
【例3-1】 已知向量a=(2,1),b=(1,-2),若ma+nb=(9,-8) (m,n∈R),则m-n的值为________.
答案 -3方向2 向量运算与平面几何的综合应用
【例3-2】已知平面上三点的坐标分别为A(-2,1),B(-1,3),C(3,4),求点D的坐标,使这四点构成平行四边形的四个顶点. 规律方法 坐标形式下向量相等的条件及其应用
(1)条件:相等向量的对应坐标相等.
(2)应用:利用坐标形式下向量相等的条件,可以建立相等关系,由此可以求出某些参数的值或点的坐标.课堂达标 答案 A 答案 A 答案 A 答案 (0,2)1.在平面直角坐标系中,平面内的点、以原点为起点的向量、有序实数对三者之间建立一一对应关系.关系图如图所示.课堂小结2.向量的坐标和这个向量的终点的坐标不一定相同.当且仅当向量的起点在原点时,向量的坐标才和这个终点的坐标相同.
3.向量坐标形式的计算,要牢记公式,细心计算,防止符号错误.
