高中数学必修4第一章 三角函数章末复习课1:54张PPT
文档属性
| 名称 | 高中数学必修4第一章 三角函数章末复习课1:54张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 21:15:14 | ||
图片预览







文档简介
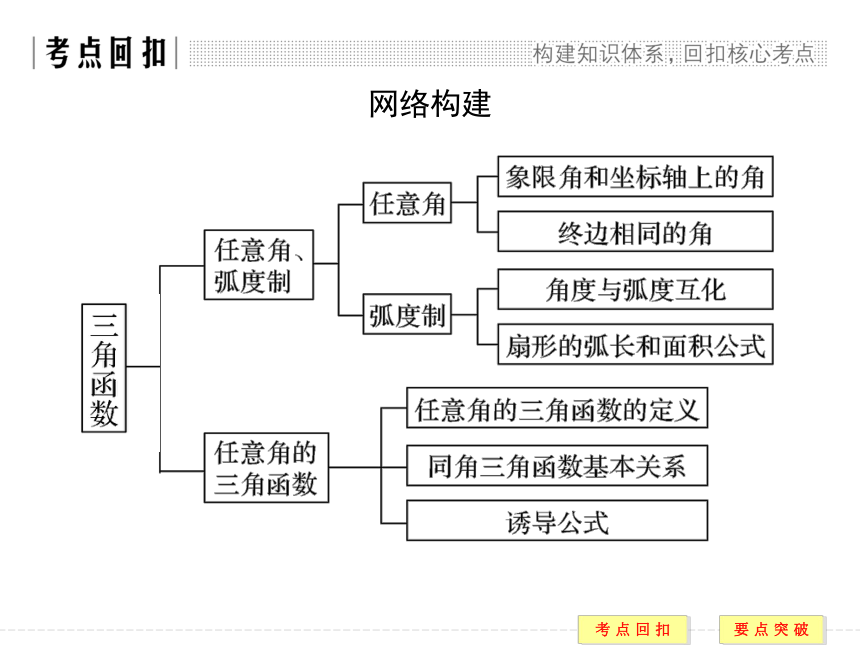
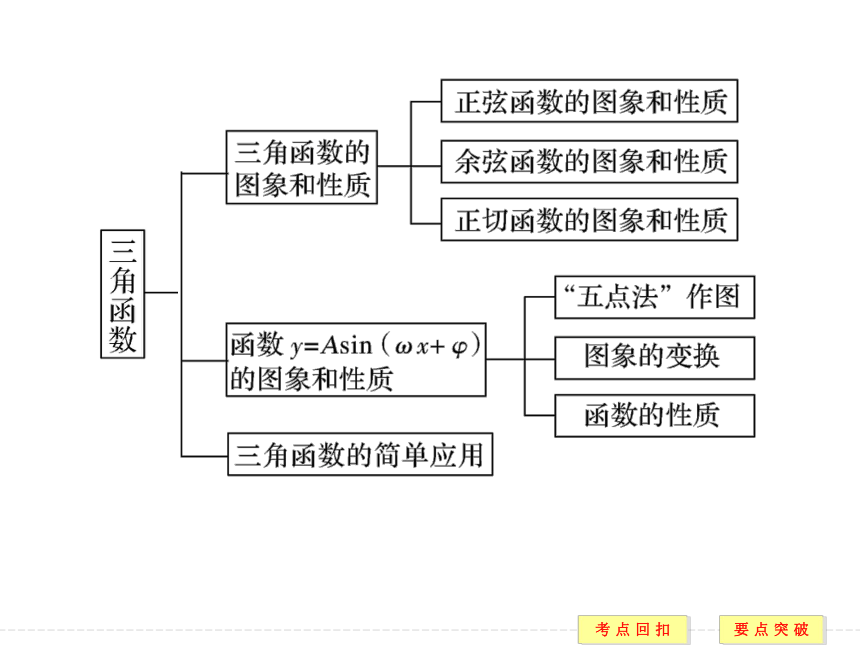
课件54张PPT。章末复习课网络构建核心归纳5.三角函数的图象
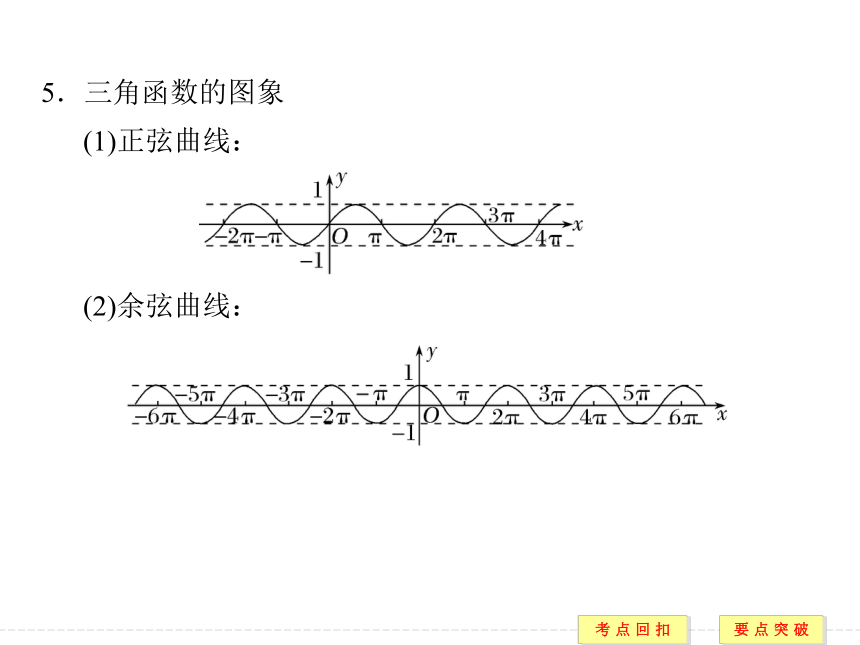
(1)正弦曲线:
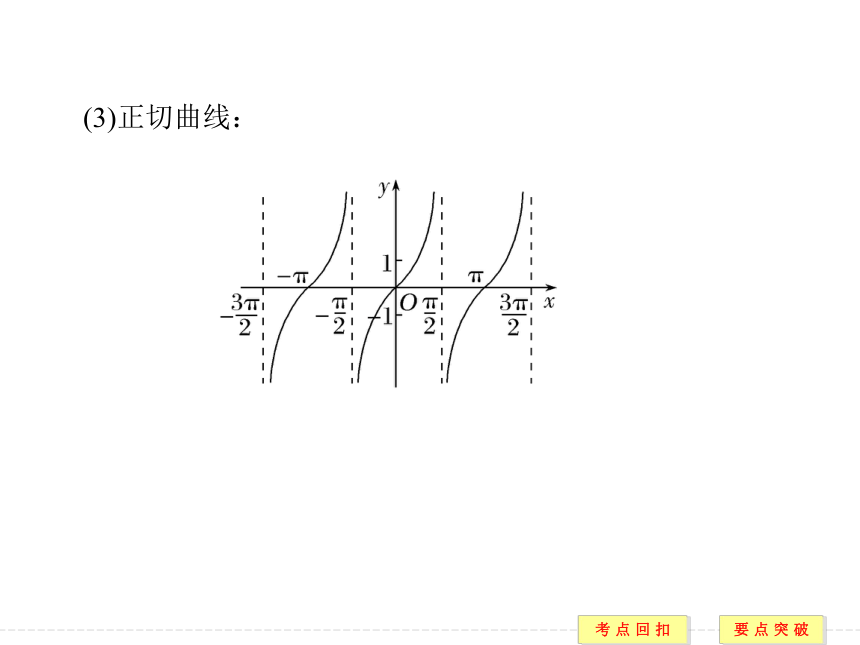
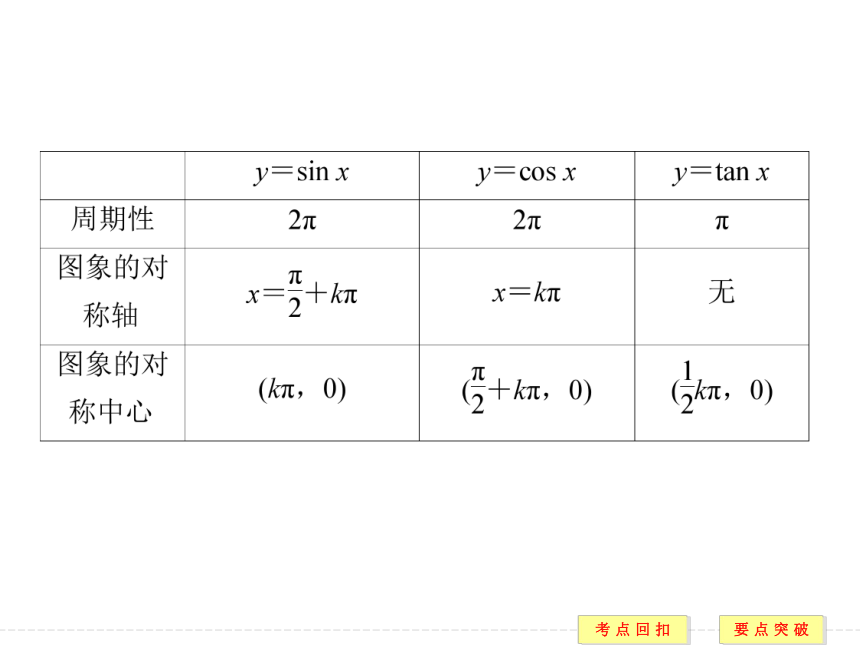
(2)余弦曲线: (3)正切曲线:6.三角函数的性质(表中k∈Z)要点一 任意角三角函数的定义【例1】 已知角α的终边经过点P(3m-9,m+2).
(1)若m=2,求5sin α+3tan α的值;
(2)若cos α≤0,且sin α>0,求实数m的取值范围.要点三 诱导公式的应用要点四 三角函数的图象 答案 A (2)描点,连线,如图所示. 由函数y=sin x的图象通过变换得到函数y=Asin(ωx+φ)的图象的两种方法要点五 三角函数图象的变换 答案 A 答案 D2.求三角函数值域(最值)的方法
(1)利用sin x,cos x的有界性.
(2)从y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域.
(3)换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.
特别提醒:利用换元法求三角函数的值域时,一定要注意三角函数自身的取值范围,否则会出现错误.3.求三角函数的单调区间
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(A>0,ω>0)的函数的单调区间可以通过解不等式方法去解答,即把ωx+φ视为一个“整体”,分别与正弦函数y=sin x,余弦函数y=cos x的单调递增(减)区间对应解出x,即得所求的单调递增(减)区间. 答案 B 答案 C
(1)正弦曲线:
(2)余弦曲线: (3)正切曲线:6.三角函数的性质(表中k∈Z)要点一 任意角三角函数的定义【例1】 已知角α的终边经过点P(3m-9,m+2).
(1)若m=2,求5sin α+3tan α的值;
(2)若cos α≤0,且sin α>0,求实数m的取值范围.要点三 诱导公式的应用要点四 三角函数的图象 答案 A (2)描点,连线,如图所示. 由函数y=sin x的图象通过变换得到函数y=Asin(ωx+φ)的图象的两种方法要点五 三角函数图象的变换 答案 A 答案 D2.求三角函数值域(最值)的方法
(1)利用sin x,cos x的有界性.
(2)从y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域.
(3)换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.
特别提醒:利用换元法求三角函数的值域时,一定要注意三角函数自身的取值范围,否则会出现错误.3.求三角函数的单调区间
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(A>0,ω>0)的函数的单调区间可以通过解不等式方法去解答,即把ωx+φ视为一个“整体”,分别与正弦函数y=sin x,余弦函数y=cos x的单调递增(减)区间对应解出x,即得所求的单调递增(减)区间. 答案 B 答案 C
