高中数学必修4第二章 平面向量章末复习课2:24张PPT
文档属性
| 名称 | 高中数学必修4第二章 平面向量章末复习课2:24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 21:14:39 | ||
图片预览








文档简介
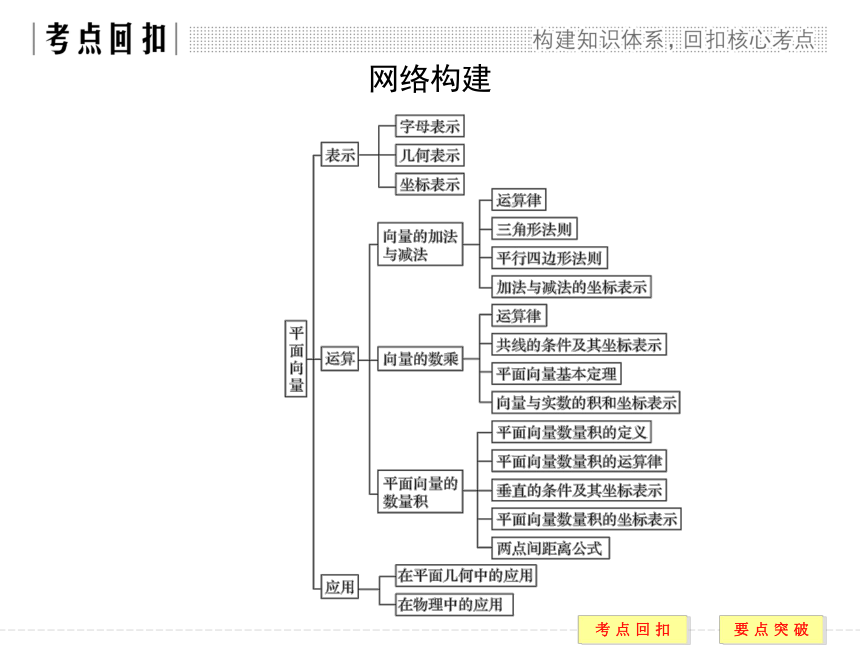
课件24张PPT。章末复习课网络构建1.五种常见的向量
(1)单位向量:模为1的向量.
(2)零向量:模为0的向量.
(3)平行(共线)向量:方向相同或相反的向量.
(4)相等向量:模相等,方向相同的向量.
(5)相反向量:模相等,方向相反的向量.核心归纳2.两个重要定理
(1)向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.
(2)平面向量基本定理:如果e1,e2是同一个平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1,e2是一组基底.
3.两个非零向量平行、垂直的等价条件
若a=(x1,y1),b=(x2,y2),则:
(1)a∥b?a=λb(λ≠0)?x1y2-x2y1=0,
(2)a⊥b?a·b=0?x1x2+y1y2=0.6.向量的运算律
(1)交换律:a+b=b+a,a·b=b·a.
(2)结合律:a+b+c=(a+b)+c,a-b-c=a-(b+c),(λa)·b=λ(a·b)=a·(λb).
(3)分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb,(a+b)·c=a·c+b·c.
(4)重要公式:(a+b)·(a-b)=a2-b2,(a±b)2=a2±2a·b+b2. 向量线性运算的基本原则和求解策略
(1)基本原则:
向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.要点一 平面向量的线性运算及应用 (2)求解策略:
①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.【例1】 (1)已知向量a=(2,1),b=(-3,4),则2a-b的结果是( )
A.(7,-2) B.(1,-2)
C.(1,-3) D.(7,2)
解析 ∵a=(2,1),b=(-3,4),∴2a-b=2(2,1)-(-3,4)=(4,2)-(-3,4)=(4+3,2-4)=(7,-2),故选A.
答案 A 答案 D 向量数量积的两种运算方法
(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a||b|cos〈a,b〉.
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
运用两向量的数量积解决长度、夹角、垂直等问题,解题时应灵活选择相应公式求解.要点二 平面向量的数量积运算 答案 5 答案 -6要点三 平面向量的平行与垂直问题
1.证明共线问题常用的方法
(1)向量a,b(a≠0)共线?存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线?x1y2-x2y1=0.
(3)向量a与b共线?存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b?a·b=0?x1x2+y1y2=0,
其中a=(x1,y1),b=(x2,y2). 答案 B要点四 平面向量的模与夹角 答案 1 答案 (2,+∞) 答案 C
(1)单位向量:模为1的向量.
(2)零向量:模为0的向量.
(3)平行(共线)向量:方向相同或相反的向量.
(4)相等向量:模相等,方向相同的向量.
(5)相反向量:模相等,方向相反的向量.核心归纳2.两个重要定理
(1)向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.
(2)平面向量基本定理:如果e1,e2是同一个平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1,e2是一组基底.
3.两个非零向量平行、垂直的等价条件
若a=(x1,y1),b=(x2,y2),则:
(1)a∥b?a=λb(λ≠0)?x1y2-x2y1=0,
(2)a⊥b?a·b=0?x1x2+y1y2=0.6.向量的运算律
(1)交换律:a+b=b+a,a·b=b·a.
(2)结合律:a+b+c=(a+b)+c,a-b-c=a-(b+c),(λa)·b=λ(a·b)=a·(λb).
(3)分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb,(a+b)·c=a·c+b·c.
(4)重要公式:(a+b)·(a-b)=a2-b2,(a±b)2=a2±2a·b+b2. 向量线性运算的基本原则和求解策略
(1)基本原则:
向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.要点一 平面向量的线性运算及应用 (2)求解策略:
①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.【例1】 (1)已知向量a=(2,1),b=(-3,4),则2a-b的结果是( )
A.(7,-2) B.(1,-2)
C.(1,-3) D.(7,2)
解析 ∵a=(2,1),b=(-3,4),∴2a-b=2(2,1)-(-3,4)=(4,2)-(-3,4)=(4+3,2-4)=(7,-2),故选A.
答案 A 答案 D 向量数量积的两种运算方法
(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a||b|cos〈a,b〉.
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
运用两向量的数量积解决长度、夹角、垂直等问题,解题时应灵活选择相应公式求解.要点二 平面向量的数量积运算 答案 5 答案 -6要点三 平面向量的平行与垂直问题
1.证明共线问题常用的方法
(1)向量a,b(a≠0)共线?存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线?x1y2-x2y1=0.
(3)向量a与b共线?存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b?a·b=0?x1x2+y1y2=0,
其中a=(x1,y1),b=(x2,y2). 答案 B要点四 平面向量的模与夹角 答案 1 答案 (2,+∞) 答案 C
