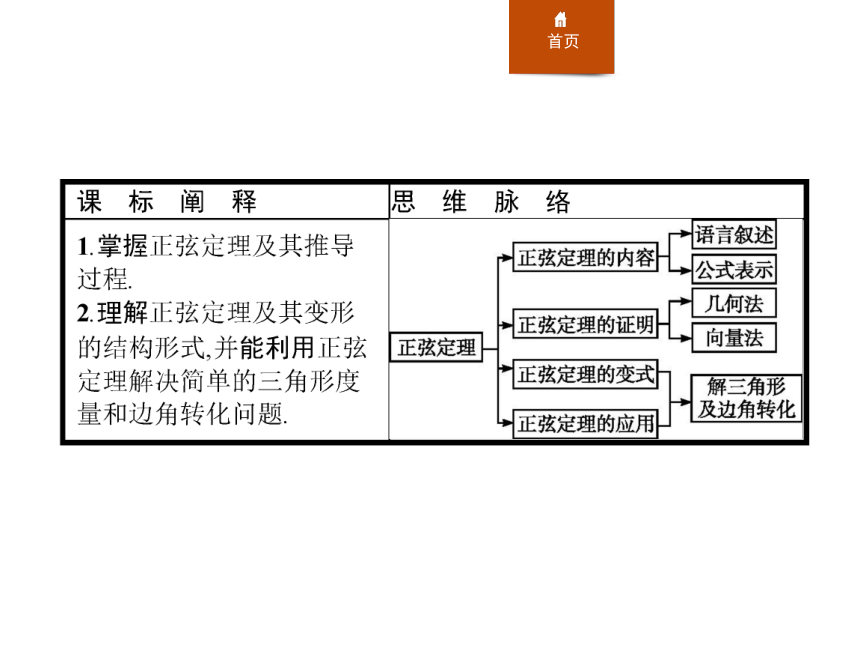
1.1.1 正弦定理:33张PPT
文档属性
| 名称 | 1.1.1 正弦定理:33张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 00:00:00 | ||
图片预览









文档简介
课件33张PPT。1.1.1 正弦定理一二一、正弦定理
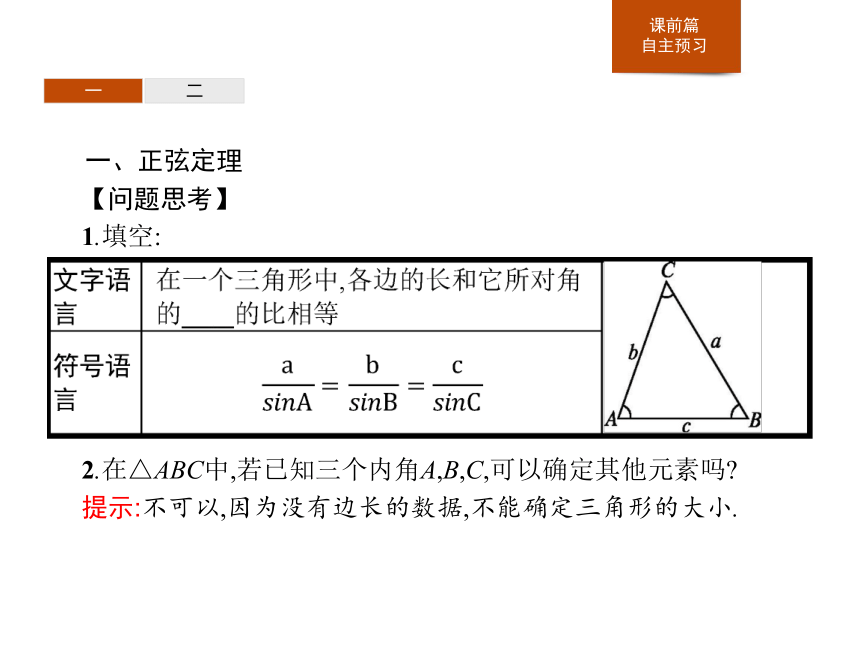
【问题思考】
1.填空:2.在△ABC中,若已知三个内角A,B,C,可以确定其他元素吗?
提示:不可以,因为没有边长的数据,不能确定三角形的大小.一二答案:B 一二二、正弦定理的适用范围
【问题思考】
1.填空:
利用正弦定理,可解决两类解三角形的问题:
(1)已知两角和任一边,求其他的边和角;
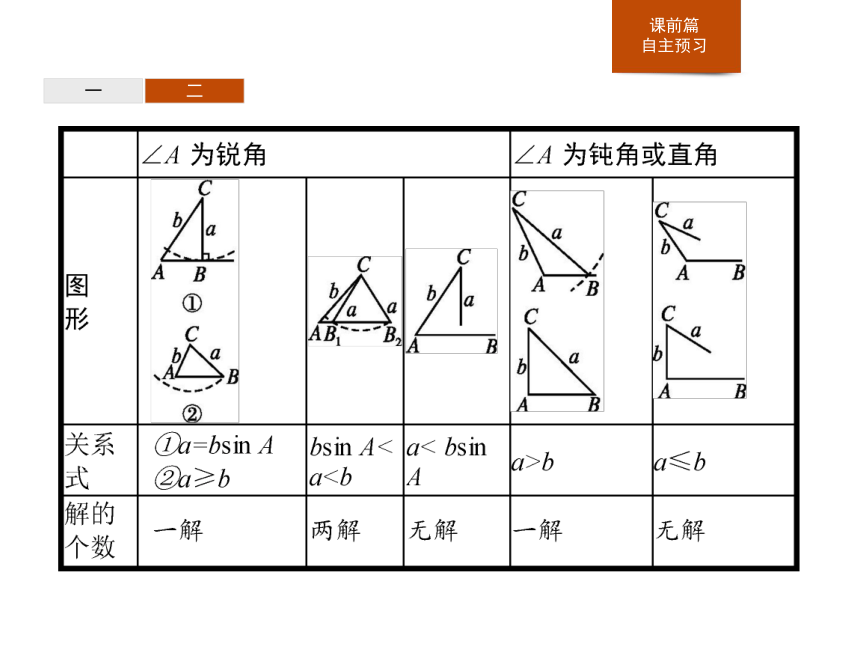
(2)已知两边和其中一边的对角,求另一边的对角,进而求出其他的边和角.一二2.如何判断三角形解的个数?
提示:(1)代数法
在△ABC中,已知a,b,∠A,由正弦定理可得sin B= sin A=m.
①当sin B>1时,这样的∠B不存在,即三角形无解.
②当sin B=1时,∠B=90°,若∠A<90°,则三角形有一解,否则无解.
③当sin B<1时,满足sin B=m的角有两个,其中设锐角为α,钝角为β,则当∠A+α>180°时,三角形无解;当∠A+α<180°,且∠A+β<180°时,有两解;当∠A+α<180°,且∠A+β>180°时有一解.一二(2)几何法
根据条件中∠A的大小,分为锐角、直角、钝角三种情况,通过几何作图,得出解的情况.作出已知∠A,以点A为圆心,边长b为半径画弧交∠A的一边于点C.使未知的边AB水平,顶点C在边AB上方,以点C为圆心,边长a为半径作圆,该圆与射线AB交点的个数,即为解的个数,如下表所示:一二一二答案:1 一二思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)正弦定理仅适用于解锐角或钝角三角形. ( )
(2)已知三角形的两角和一边,这样的三角形是唯一的. ( )
(3)已知三角形的两边和一角,这样的三角形至多有两解. ( )
(4)在△ABC中,若∠A>∠B,则sin A>sin B. ( )
(5)在△ABC中,若∠A+∠B> ,则有sin A>cos B成立. ( )
答案:(1)× (2)√ (3)√ (4)√ (5)×探究一探究二探究三探究四探究五当堂检测正弦定理的简单应用
【例1】 (1)在△ABC中,∠B=30°,∠C=45°,c=1,求b的长及△ABC外接圆的半径.
(2)在△ABC中,a= ,b=6,∠A=30°,解此三角形.探究一探究二探究三探究四探究五当堂检测反思感悟1.解三角形第一类问题(即已知两角和一边,求另两边和一角)的方法步骤,即先利用内角和公式求得第三角,再由正弦定理求得已知角的对边,最后用正弦定理求第三边.
2.解三角形第二类问题(即已知两边和其中一边的对角,求另一边的对角及其他的角和边)的方法步骤,即先由正弦定理求得已知边的对角,再利用内角和公式求得第三角,最后求得第三边.解答此类问题应注意对解的个数的讨论.探究一探究二探究三探究四探究五当堂检测若将本例1(2)中的条件改为“b=4,c=8,∠B=30°”,结果如何?探究一探究二探究三探究四探究五当堂检测判断三角形的形状
【例2】在△ABC中,若sin2A=sin2B+sin2C,sin A=2sin B·cos C,试判断△ABC的形状.
思路分析:本题考查了利用正弦定理判断三角形的形状问题.探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测答案:(1)等边三角形
(2)等腰直角三角形 探究一探究二探究三探究四探究五当堂检测判断三角形解的个数
【例3】 判断下列三角形是否有解,若有,则作出解答.
(1)a=7,b=8,∠A=105°;
(2)b=10,c= ,∠C=60°.
思路分析:结合三角形中大边对大角以及前面总结的有解、无解的结论来确定.
解:(1)∵a=7,b=8,a90°,∴本题无解.探究一探究二探究三探究四探究五当堂检测反思感悟已知两边及其中一边的对角时,三角形的解的情况不确定(见下表).探究一探究二探究三探究四探究五当堂检测用正弦定理证明问题
【例4】 在△ABC中,求证:
思路分析:求证的等式左边既有边又有角,而右边只有角,可利用正弦定理将左边的边化成角.
证明:由正弦定理,得探究一探究二探究三探究四探究五当堂检测反思感悟在含有边角关系的等式中,若含有a,b,c及sin A,sin B,sin C的形式,则可利用正弦定理并结合已知条件及目标完成边角转化,在转化过程中往往会用到三角变换公式,还要注意△ABC中的隐含条件∠A+∠B+∠C=180°.探究一探究二探究三探究四探究五当堂检测变式训练2在△ABC中,已知a2tan B=b2tan A,求证:△ABC为等腰三角形或直角三角形.探究一探究二探究三探究四探究五当堂检测正弦定理与三角函数知识的综合应用 思路分析:本题考查了三角函数的性质、三角恒等变换,以及正弦定理.
(1)利用辅助角公式将f(x)化简后可求得周期和值域;
(2)由f(A)= 可求得角A,先利用正弦定理可求得角B,再利用三角形内角和定理求得角C.探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测反思感悟1.高考中解三角形的知识往往与三角函数知识进行交叉考查,涉及解三角形的问题,求最值或取值范围是一种常见题型.
2.解决三角形中的有关最值问题或取值范围问题的关键在于:利用正弦定理、三角恒等变换将有关问题转化为某一个角的三角函数或某一边的函数,进而求出其最值或取值范围.探究一探究二探究三探究四探究五当堂检测变式训练3在锐角三角形ABC中,角A,B,C分别对应边a,b,c,且a=2bsin A,求cos A+sin C的取值范围.
思路分析:先将cos A+sin C转化成关于∠A或∠C的三角函数,再求三角函数的取值范围.
解:在锐角三角形ABC中,根据正弦定理,a=2Rsin A,b=2Rsin B(R为△ABC外接圆的半径),探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测1.在△ABC中,根据下列条件解三角形,其中有两解的是 ( )
A.b=10,∠A=45°,∠C=70°
B.a=30,b=25,∠A=150°
C.a=7,b=8,∠A=98°
D.a=14,b=16,∠A=45°
解析:对于A项,由三角形全等的判定知识得只有一解;
对于B项,∵a>b,∴∠A>∠B,
又∠A=150°,∴只有一解;
对于C项,∵a又∵∠A>90°,∴无解;∴有两解.
答案:D探究一探究二探究三探究四探究五当堂检测2.设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B =asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
解析:∵bcos C+ccos B=asin A,
由正弦定理,得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,即sin A=sin2A.
又sin A>0,∴sin A=1,
又∠A∈(0,π),∴∠A= ,
故△ABC为直角三角形.
答案:B探究一探究二探究三探究四探究五当堂检测答案:60°或120° 探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测
【问题思考】
1.填空:2.在△ABC中,若已知三个内角A,B,C,可以确定其他元素吗?
提示:不可以,因为没有边长的数据,不能确定三角形的大小.一二答案:B 一二二、正弦定理的适用范围
【问题思考】
1.填空:
利用正弦定理,可解决两类解三角形的问题:
(1)已知两角和任一边,求其他的边和角;
(2)已知两边和其中一边的对角,求另一边的对角,进而求出其他的边和角.一二2.如何判断三角形解的个数?
提示:(1)代数法
在△ABC中,已知a,b,∠A,由正弦定理可得sin B= sin A=m.
①当sin B>1时,这样的∠B不存在,即三角形无解.
②当sin B=1时,∠B=90°,若∠A<90°,则三角形有一解,否则无解.
③当sin B<1时,满足sin B=m的角有两个,其中设锐角为α,钝角为β,则当∠A+α>180°时,三角形无解;当∠A+α<180°,且∠A+β<180°时,有两解;当∠A+α<180°,且∠A+β>180°时有一解.一二(2)几何法
根据条件中∠A的大小,分为锐角、直角、钝角三种情况,通过几何作图,得出解的情况.作出已知∠A,以点A为圆心,边长b为半径画弧交∠A的一边于点C.使未知的边AB水平,顶点C在边AB上方,以点C为圆心,边长a为半径作圆,该圆与射线AB交点的个数,即为解的个数,如下表所示:一二一二答案:1 一二思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)正弦定理仅适用于解锐角或钝角三角形. ( )
(2)已知三角形的两角和一边,这样的三角形是唯一的. ( )
(3)已知三角形的两边和一角,这样的三角形至多有两解. ( )
(4)在△ABC中,若∠A>∠B,则sin A>sin B. ( )
(5)在△ABC中,若∠A+∠B> ,则有sin A>cos B成立. ( )
答案:(1)× (2)√ (3)√ (4)√ (5)×探究一探究二探究三探究四探究五当堂检测正弦定理的简单应用
【例1】 (1)在△ABC中,∠B=30°,∠C=45°,c=1,求b的长及△ABC外接圆的半径.
(2)在△ABC中,a= ,b=6,∠A=30°,解此三角形.探究一探究二探究三探究四探究五当堂检测反思感悟1.解三角形第一类问题(即已知两角和一边,求另两边和一角)的方法步骤,即先利用内角和公式求得第三角,再由正弦定理求得已知角的对边,最后用正弦定理求第三边.
2.解三角形第二类问题(即已知两边和其中一边的对角,求另一边的对角及其他的角和边)的方法步骤,即先由正弦定理求得已知边的对角,再利用内角和公式求得第三角,最后求得第三边.解答此类问题应注意对解的个数的讨论.探究一探究二探究三探究四探究五当堂检测若将本例1(2)中的条件改为“b=4,c=8,∠B=30°”,结果如何?探究一探究二探究三探究四探究五当堂检测判断三角形的形状
【例2】在△ABC中,若sin2A=sin2B+sin2C,sin A=2sin B·cos C,试判断△ABC的形状.
思路分析:本题考查了利用正弦定理判断三角形的形状问题.探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测答案:(1)等边三角形
(2)等腰直角三角形 探究一探究二探究三探究四探究五当堂检测判断三角形解的个数
【例3】 判断下列三角形是否有解,若有,则作出解答.
(1)a=7,b=8,∠A=105°;
(2)b=10,c= ,∠C=60°.
思路分析:结合三角形中大边对大角以及前面总结的有解、无解的结论来确定.
解:(1)∵a=7,b=8,a
【例4】 在△ABC中,求证:
思路分析:求证的等式左边既有边又有角,而右边只有角,可利用正弦定理将左边的边化成角.
证明:由正弦定理,得探究一探究二探究三探究四探究五当堂检测反思感悟在含有边角关系的等式中,若含有a,b,c及sin A,sin B,sin C的形式,则可利用正弦定理并结合已知条件及目标完成边角转化,在转化过程中往往会用到三角变换公式,还要注意△ABC中的隐含条件∠A+∠B+∠C=180°.探究一探究二探究三探究四探究五当堂检测变式训练2在△ABC中,已知a2tan B=b2tan A,求证:△ABC为等腰三角形或直角三角形.探究一探究二探究三探究四探究五当堂检测正弦定理与三角函数知识的综合应用 思路分析:本题考查了三角函数的性质、三角恒等变换,以及正弦定理.
(1)利用辅助角公式将f(x)化简后可求得周期和值域;
(2)由f(A)= 可求得角A,先利用正弦定理可求得角B,再利用三角形内角和定理求得角C.探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测反思感悟1.高考中解三角形的知识往往与三角函数知识进行交叉考查,涉及解三角形的问题,求最值或取值范围是一种常见题型.
2.解决三角形中的有关最值问题或取值范围问题的关键在于:利用正弦定理、三角恒等变换将有关问题转化为某一个角的三角函数或某一边的函数,进而求出其最值或取值范围.探究一探究二探究三探究四探究五当堂检测变式训练3在锐角三角形ABC中,角A,B,C分别对应边a,b,c,且a=2bsin A,求cos A+sin C的取值范围.
思路分析:先将cos A+sin C转化成关于∠A或∠C的三角函数,再求三角函数的取值范围.
解:在锐角三角形ABC中,根据正弦定理,a=2Rsin A,b=2Rsin B(R为△ABC外接圆的半径),探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测1.在△ABC中,根据下列条件解三角形,其中有两解的是 ( )
A.b=10,∠A=45°,∠C=70°
B.a=30,b=25,∠A=150°
C.a=7,b=8,∠A=98°
D.a=14,b=16,∠A=45°
解析:对于A项,由三角形全等的判定知识得只有一解;
对于B项,∵a>b,∴∠A>∠B,
又∠A=150°,∴只有一解;
对于C项,∵a
答案:D探究一探究二探究三探究四探究五当堂检测2.设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B =asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
解析:∵bcos C+ccos B=asin A,
由正弦定理,得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,即sin A=sin2A.
又sin A>0,∴sin A=1,
又∠A∈(0,π),∴∠A= ,
故△ABC为直角三角形.
答案:B探究一探究二探究三探究四探究五当堂检测答案:60°或120° 探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测探究一探究二探究三探究四探究五当堂检测
