1.2 解直角三角形应用举例:38张PPT
文档属性
| 名称 | 1.2 解直角三角形应用举例:38张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 21:21:30 | ||
图片预览









文档简介
课件38张PPT。1.2 应用举例一二三一、实际应用问题中的有关术语
【问题思考】
1.填空:
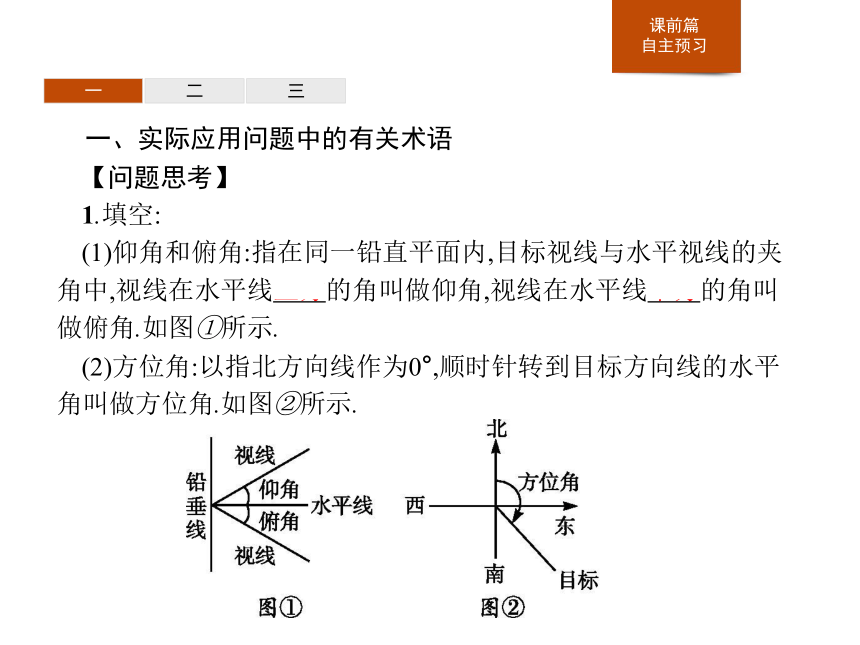
(1)仰角和俯角:指在同一铅直平面内,目标视线与水平视线的夹角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.如图①所示.
(2)方位角:以指北方向线作为0°,顺时针转到目标方向线的水平角叫做方位角.如图②所示.一二三(3)方向角:相对于某一正方向的水平角,如北偏东60°.
(4)坡角与坡度:坡面与水平面的夹角叫做坡角,坡面的铅直高度h与水平宽度l的比叫做坡度(或坡比).
设坡角为α,坡度为i,则i= =tan α,如图③所示.?一二三2.仰角、俯角、方位角有什么区别?
提示:三者的参照不同,仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.
3.做一做:从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
解析:要正确理解仰角、俯角的含义,准确地找出仰角、俯角的确切位置,如图,从A处望B处的仰角α与从B处望A处的俯角β是内错角(根据水平线平行),即α=β.
?
答案:B一二三二、三角形中的有关公式和结论
【问题思考】
1.填空:
(1)在直角三角形中各元素间的关系.
在△ABC中,若∠C=90°,AB=c,AC=b,BC=a,则有,
①锐角之间的关系:∠A+∠B=90°.
②三边之间的关系:a2+b2=c2 .
③边角之间的关系:(锐角三角函数的定义)一二三(2)斜三角形中各元素间的关系.
在△ABC中,若角A,B,C为其内角,a,b,c分别表示角A,B,C的对边,则有,
①角与角之间的关系:∠A+∠B+∠C=π;sin Acos B,sin B>cos C,sin C>cos A.
②边与边之间的关系:a+b>c,b+c>a,c+a>b,a-b③边角之间的关系.
正弦定理:_____________________ (R为△ABC外接圆的半径).
余弦定理:c2=a2+b2-2abcos C,b2=a2+c2-2accos B,a2=b2+c2-2bccos A.一二三(3)三角形中的角的变换及面积公式.
①角的变换.
因为在△ABC中,∠A+∠B+∠C=π,
所以sin(A+B)=sin C ;cos(A+B)=-cos C ;tan(A+B)=-tan C .一二三一二三答案:B 一二三三、解应用题的一般思路
【问题思考】
1.填空:
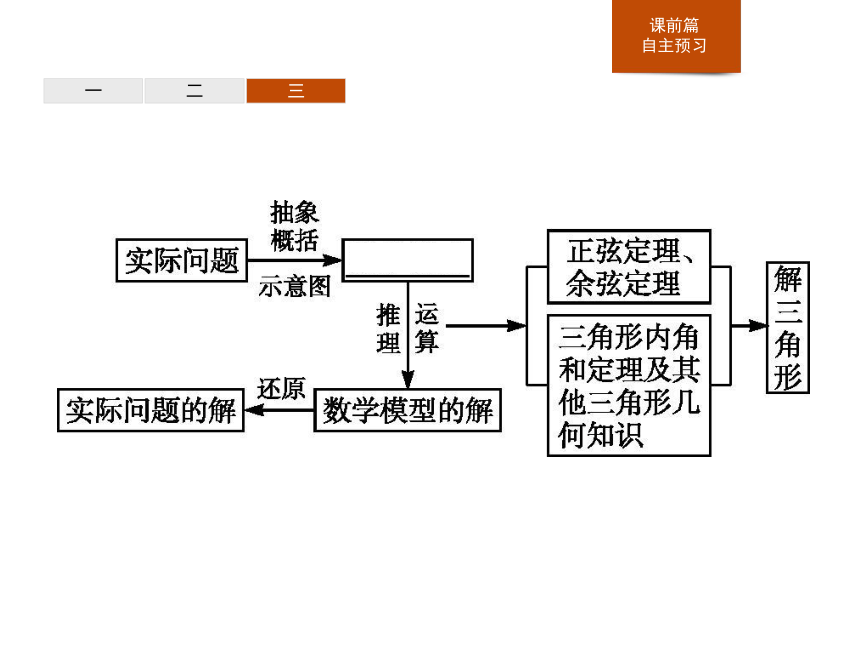
(1)读懂题意,理解问题的实际背景,明确已知和所求,理清量与量之间的关系.
(2)根据题意画出示意图,把已知和要求的量尽量集中到有关三角形中,将实际问题抽象成解三角形模型.
(3)选择正弦定理或余弦定理求解.
(4)将三角形的解还原为实际问题的解,注意实际问题中单位、近似计算的要求.这一思路描述如下:一二三一二三2.做一做:如图,某炮兵阵地位于点A,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离为 . (精确到0.01 km)?一二三解析:∵在△BCD中,∠CDB=45°,∠BCD=75°,
∴∠CBD=180°-∠BCD-∠CDB=60°.答案:2.91 km 一二三思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)方向角可以是钝角. ( )
(2)方位角可以是钝角. ( )
(3)已知三角形的两边及其夹角可以用余弦定理解三角形. ( )
(4)已知在△ABC中,a,b,c满足c2-a2-b2+ ab=0,则该三角形为锐角三角形. ( )
答案:(1)× (2)√ (3)√ (4)×探究一探究二探究三探究四当堂检测测量距离问题
【例1】 如图,隔河看两目标A,B,但不能到达,在岸边选取相距
km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°, ∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
思路分析:要求出A,B之间的距离,可在△ABC(或△ADB)中找关系,但不管在哪个三角形中,AC,BC这些量都是未知的,需要先在三角形中找出合适的关系式,求出它们的值,再解斜三角形即可.探究一探究二探究三探究四当堂检测解:在△ACD中,∵∠ADC=30°,∠ACD=75°+45°=120°,探究一探究二探究三探究四当堂检测反思感悟测量两点间距离的三种情况 求解思路如下:
(1)当A,B两点之间既不可到达也不可视时,测出两边及其夹角,运用余弦定理求解.
(2)当A,B两点之间可视但有一点不可到达时,测出两角及其夹边,先用内角和定理求第三角再运用正弦定理求解.
(3)当A,B两点都不可到达时,先在△ADC和△BDC中分别求出AD,AC和BD,BC,再在△ABC或△ABD中运用余弦定理求解.探究一探究二探究三探究四当堂检测对于例1,你还有其他解法吗?
解:在△BCD中,因为∠DCB=45°,∠BDC=75°,
所以∠CBD=60°.探究一探究二探究三探究四当堂检测测量高度问题
【例2】 某人在塔的正东沿着南偏西60°的方向前进40 m以后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.
思路分析:设塔顶为A,塔底为B,该人从点C前进40 m后到达点D,设在CD上点E处望塔顶的仰角最大,此时应有AE⊥CD,则∠AEB=30°.为求AB,先求BE,在△BCD中,BE⊥CD,结合条件解三角形可求出BE.探究一探究二探究三探究四当堂检测解:依题意画图,某人在C处,AB为塔高,他沿CD前进,CD=40 m,
此时∠DBF=45°,探究一探究二探究三探究四当堂检测反思感悟求AB的高度分为以下三类 求解思路如下:
(1)当BC底部可到达时,利用直角三角形的边角关系求解,则AB=atan C.
(2)当BD不可到达时,利用Rt△ABD和Rt△ABD的边角关系,表达出边a,AB与∠ACB,∠ADB之间的关系.
(3)当BC,BD均不可到达时,则利用△BCD和△ABC及正弦定理求解.探究一探究二探究三探究四当堂检测变式训练1如图,在测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.探究一探究二探究三探究四当堂检测测量角度问题
【例3】 如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在北偏东45°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时10海里的速度沿南偏东75°方向前进,若红方侦察艇以每小时14海里的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.思路分析:假设经过x小时后在C处追上蓝方的小艇,作出示意图,把实际数据转化到三角形中,利用正、余弦定理求解.探究一探究二探究三探究四当堂检测解:如图,设红方侦察艇经过x小时后在C处追上蓝方的小艇,
则AC=14x海里,BC=10x海里,∠ABC=120°.探究一探究二探究三探究四当堂检测反思感悟解决追及问题的步骤:
(1)把实际问题转化为数学问题;
(2)画出表示实际问题的图形,并在图中标出有关的角和距离,这样借助于正弦定理或余弦定理,就容易解决问题了;
(3)把数学问题还原到实际问题中去.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测面积问题
【例4】 在半径为R的扇形OAB中,圆心角∠AOB=60°,在扇形内有一个内接矩形,求内接矩形的最大面积.
思路分析:扇形的内接矩形有且仅有两种类型:一种是矩形的一边与扇形的一条半径重合;另一种是以扇形的对称轴为对称轴的矩形.我们分别求出这两种类型的矩形的最大面积,再取两者中较大的,就是符合条件的最大面积.探究一探究二探究三探究四当堂检测解:如图①所示,设PQ=x,MP=y,则矩形的面积S=xy.
连接ON,令∠AON=θ,则y=Rsin θ.
在△OMN中,利用正弦定理,得探究一探究二探究三探究四当堂检测反思感悟关于求面积最值问题,关键是将面积函数表达出来,先根据已知条件利用正弦定理将与矩形面积有关的量求出,再转化为求三角函数最值问题,这是这一类问题常用的解题思路.探究一探究二探究三探究四当堂检测变式训练3如图,公园内有一块边长为2a的等边三角形ABC形状的土地,现修成草坪,图中DE把草坪分成面积相等的两部分,点D在AB上,点E在AC上.
(1)设AD=x(x≥a),DE=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本希望它最短,那么DE的位置应该在哪里?如果DE是参观线路,那么希望它最长,DE的位置又应该在哪里?探究一探究二探究三探究四当堂检测解:(1)∵在△ABC中,点D在AB上,
∴a≤x≤2a.探究一探究二探究三探究四当堂检测∵a2≤t1∴t1t2>0,t1-t2<0,a4∴f(t1)-f(t2)>0,∴f(t1)>f(t2).
∴f(t)在区间[a2,2a2)内是减函数,
同理f(t)在区间[2a2,4a2]上是增函数.
又f(a2)=3a2,f(2a2)=2a2,f(4a2)=3a2.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测1.如图,在河岸AC测量河的宽度BC,测量下列四组数据,较适宜的是( )
?
A.a和c B.c和b
C.c和β D.b和α
解析:在河的一岸测量河的宽度,关键是选准基线,在本题中AC可看做基线,在△ABC中,能够测量到的分别为边b和角α.
答案:D探究一探究二探究三探究四当堂检测2.如图,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )解析:显然∠ACB=120°,AC=BC=a km,则∠CAB=∠CBA=30°.答案:B 探究一探究二探究三探究四当堂检测?
【问题思考】
1.填空:
(1)仰角和俯角:指在同一铅直平面内,目标视线与水平视线的夹角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.如图①所示.
(2)方位角:以指北方向线作为0°,顺时针转到目标方向线的水平角叫做方位角.如图②所示.一二三(3)方向角:相对于某一正方向的水平角,如北偏东60°.
(4)坡角与坡度:坡面与水平面的夹角叫做坡角,坡面的铅直高度h与水平宽度l的比叫做坡度(或坡比).
设坡角为α,坡度为i,则i= =tan α,如图③所示.?一二三2.仰角、俯角、方位角有什么区别?
提示:三者的参照不同,仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.
3.做一做:从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
解析:要正确理解仰角、俯角的含义,准确地找出仰角、俯角的确切位置,如图,从A处望B处的仰角α与从B处望A处的俯角β是内错角(根据水平线平行),即α=β.
?
答案:B一二三二、三角形中的有关公式和结论
【问题思考】
1.填空:
(1)在直角三角形中各元素间的关系.
在△ABC中,若∠C=90°,AB=c,AC=b,BC=a,则有,
①锐角之间的关系:∠A+∠B=90°.
②三边之间的关系:a2+b2=c2 .
③边角之间的关系:(锐角三角函数的定义)一二三(2)斜三角形中各元素间的关系.
在△ABC中,若角A,B,C为其内角,a,b,c分别表示角A,B,C的对边,则有,
①角与角之间的关系:∠A+∠B+∠C=π;sin A
②边与边之间的关系:a+b>c,b+c>a,c+a>b,a-b
正弦定理:_____________________ (R为△ABC外接圆的半径).
余弦定理:c2=a2+b2-2abcos C,b2=a2+c2-2accos B,a2=b2+c2-2bccos A.一二三(3)三角形中的角的变换及面积公式.
①角的变换.
因为在△ABC中,∠A+∠B+∠C=π,
所以sin(A+B)=sin C ;cos(A+B)=-cos C ;tan(A+B)=-tan C .一二三一二三答案:B 一二三三、解应用题的一般思路
【问题思考】
1.填空:
(1)读懂题意,理解问题的实际背景,明确已知和所求,理清量与量之间的关系.
(2)根据题意画出示意图,把已知和要求的量尽量集中到有关三角形中,将实际问题抽象成解三角形模型.
(3)选择正弦定理或余弦定理求解.
(4)将三角形的解还原为实际问题的解,注意实际问题中单位、近似计算的要求.这一思路描述如下:一二三一二三2.做一做:如图,某炮兵阵地位于点A,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离为 . (精确到0.01 km)?一二三解析:∵在△BCD中,∠CDB=45°,∠BCD=75°,
∴∠CBD=180°-∠BCD-∠CDB=60°.答案:2.91 km 一二三思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)方向角可以是钝角. ( )
(2)方位角可以是钝角. ( )
(3)已知三角形的两边及其夹角可以用余弦定理解三角形. ( )
(4)已知在△ABC中,a,b,c满足c2-a2-b2+ ab=0,则该三角形为锐角三角形. ( )
答案:(1)× (2)√ (3)√ (4)×探究一探究二探究三探究四当堂检测测量距离问题
【例1】 如图,隔河看两目标A,B,但不能到达,在岸边选取相距
km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°, ∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
思路分析:要求出A,B之间的距离,可在△ABC(或△ADB)中找关系,但不管在哪个三角形中,AC,BC这些量都是未知的,需要先在三角形中找出合适的关系式,求出它们的值,再解斜三角形即可.探究一探究二探究三探究四当堂检测解:在△ACD中,∵∠ADC=30°,∠ACD=75°+45°=120°,探究一探究二探究三探究四当堂检测反思感悟测量两点间距离的三种情况 求解思路如下:
(1)当A,B两点之间既不可到达也不可视时,测出两边及其夹角,运用余弦定理求解.
(2)当A,B两点之间可视但有一点不可到达时,测出两角及其夹边,先用内角和定理求第三角再运用正弦定理求解.
(3)当A,B两点都不可到达时,先在△ADC和△BDC中分别求出AD,AC和BD,BC,再在△ABC或△ABD中运用余弦定理求解.探究一探究二探究三探究四当堂检测对于例1,你还有其他解法吗?
解:在△BCD中,因为∠DCB=45°,∠BDC=75°,
所以∠CBD=60°.探究一探究二探究三探究四当堂检测测量高度问题
【例2】 某人在塔的正东沿着南偏西60°的方向前进40 m以后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.
思路分析:设塔顶为A,塔底为B,该人从点C前进40 m后到达点D,设在CD上点E处望塔顶的仰角最大,此时应有AE⊥CD,则∠AEB=30°.为求AB,先求BE,在△BCD中,BE⊥CD,结合条件解三角形可求出BE.探究一探究二探究三探究四当堂检测解:依题意画图,某人在C处,AB为塔高,他沿CD前进,CD=40 m,
此时∠DBF=45°,探究一探究二探究三探究四当堂检测反思感悟求AB的高度分为以下三类 求解思路如下:
(1)当BC底部可到达时,利用直角三角形的边角关系求解,则AB=atan C.
(2)当BD不可到达时,利用Rt△ABD和Rt△ABD的边角关系,表达出边a,AB与∠ACB,∠ADB之间的关系.
(3)当BC,BD均不可到达时,则利用△BCD和△ABC及正弦定理求解.探究一探究二探究三探究四当堂检测变式训练1如图,在测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.探究一探究二探究三探究四当堂检测测量角度问题
【例3】 如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在北偏东45°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时10海里的速度沿南偏东75°方向前进,若红方侦察艇以每小时14海里的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.思路分析:假设经过x小时后在C处追上蓝方的小艇,作出示意图,把实际数据转化到三角形中,利用正、余弦定理求解.探究一探究二探究三探究四当堂检测解:如图,设红方侦察艇经过x小时后在C处追上蓝方的小艇,
则AC=14x海里,BC=10x海里,∠ABC=120°.探究一探究二探究三探究四当堂检测反思感悟解决追及问题的步骤:
(1)把实际问题转化为数学问题;
(2)画出表示实际问题的图形,并在图中标出有关的角和距离,这样借助于正弦定理或余弦定理,就容易解决问题了;
(3)把数学问题还原到实际问题中去.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测面积问题
【例4】 在半径为R的扇形OAB中,圆心角∠AOB=60°,在扇形内有一个内接矩形,求内接矩形的最大面积.
思路分析:扇形的内接矩形有且仅有两种类型:一种是矩形的一边与扇形的一条半径重合;另一种是以扇形的对称轴为对称轴的矩形.我们分别求出这两种类型的矩形的最大面积,再取两者中较大的,就是符合条件的最大面积.探究一探究二探究三探究四当堂检测解:如图①所示,设PQ=x,MP=y,则矩形的面积S=xy.
连接ON,令∠AON=θ,则y=Rsin θ.
在△OMN中,利用正弦定理,得探究一探究二探究三探究四当堂检测反思感悟关于求面积最值问题,关键是将面积函数表达出来,先根据已知条件利用正弦定理将与矩形面积有关的量求出,再转化为求三角函数最值问题,这是这一类问题常用的解题思路.探究一探究二探究三探究四当堂检测变式训练3如图,公园内有一块边长为2a的等边三角形ABC形状的土地,现修成草坪,图中DE把草坪分成面积相等的两部分,点D在AB上,点E在AC上.
(1)设AD=x(x≥a),DE=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本希望它最短,那么DE的位置应该在哪里?如果DE是参观线路,那么希望它最长,DE的位置又应该在哪里?探究一探究二探究三探究四当堂检测解:(1)∵在△ABC中,点D在AB上,
∴a≤x≤2a.探究一探究二探究三探究四当堂检测∵a2≤t1
∴f(t)在区间[a2,2a2)内是减函数,
同理f(t)在区间[2a2,4a2]上是增函数.
又f(a2)=3a2,f(2a2)=2a2,f(4a2)=3a2.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测1.如图,在河岸AC测量河的宽度BC,测量下列四组数据,较适宜的是( )
?
A.a和c B.c和b
C.c和β D.b和α
解析:在河的一岸测量河的宽度,关键是选准基线,在本题中AC可看做基线,在△ABC中,能够测量到的分别为边b和角α.
答案:D探究一探究二探究三探究四当堂检测2.如图,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )解析:显然∠ACB=120°,AC=BC=a km,则∠CAB=∠CBA=30°.答案:B 探究一探究二探究三探究四当堂检测?
