2.1.1 数列:36张PPT
文档属性
| 名称 | 2.1.1 数列:36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 756.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 00:00:00 | ||
图片预览











文档简介
课件36张PPT。2.1.1 数列一二三四一、数列的有关概念
【问题思考】
1.填空:
(1)数列的定义:按照一定次序排列起来的一列数叫做数列,数列中的每一个数都叫做这个数列的项.
(2)数列的一般形式可以写成a1,a2,a3,…,an,….其中an是数列的第n项,叫做数列的通项,一般形式的数列简记作{an},这里{an}是数列的简记符号,并不表示一个集合.
2.数列2,3,4,5,6与集合{2,3,4,5,6}有何区别?
提示:数列2,3,4,5,6是按一定的次序排列的,打乱顺序后又产生新的数列;而{2,3,4,5,6}中元素无论按怎样的顺序排列都是同一个集合.一二三四二、数列的通项公式
【问题思考】
1.填空:
如果数列{an}的第n项an与n之间的关系可以用一个函数式an=f(n)来表示,那么这个公式就叫做这个数列的通项公式.一二三四一二三四三、数列与函数的关系
【问题思考】
1.填空:
在数列{an}中,对于每一个正整数n(或n∈{1,2,…,k}),都有一个数an与之对应,因此,数列可以看成以正整数N+(或它的有限子集{1,2,…,k})为定义域的函数an=f(n),即当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.反过来,对于函数y=f(x),如果f(i)(i=1,2,3,…)有意义,那么我们可以得到一个数列f(1),f(2),f(3),…,f(n),…,其图象是一系列孤立的点.一二三四2.数列{an}与函数f(n)=an(n∈N+)的区别如何?
提示:(1)数列{an}与函数f(n)=an(n∈N+)是不同的,{an}中的元素具有有序性,如将a1,a2,a3,…,an排成a3,a1,a2,…,an,则为不同的数列,而对于函数f(n)=an(n∈N+)来说却是一样的.
(2)数列中,自变量的取值更有规律性,必须从小到大取正整数.
3.做一做:已知数列{an}的通项公式为an=n2-8n+15,则( )
A.3不是数列{an}中的项
B.3只是数列{an}中的第2项
C.3只是数列{an}中的第6项
D.3是数列{an}中的第2项或第6项
解析:令an=3,即n2-8n+15=3,解得n=2或n=6.
答案:D一二三四四、数列的分类
【问题思考】
1.填空:
(1)按项的个数分类(2)按项的变化趋势分类 一二三四2.是否存在一个各项都小于5的无穷递增数列?如果存在,请写出一个这样的数列的通项公式.3.做一做:已知下列数列:
①-1,0,1,2,3,4,…,n.
②1,-1,1,-1,….④6,6,6,6,6.
其中递增数列有 ,递减数列有 ,常数列有 ,有穷数列有 ,无穷数列有 (只填序号就可以).?
答案:① ③ ④ ①④ ②③一二三四思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)数列是按一定顺序排列的有规律的一列数. ( )
(2)数列中的项不可能相等. ( )
(3)数列是可以用图象表示的. ( )
(4)数列可以用一群孤立的点表示. ( )
(5)数列可以看成一种特殊的函数. ( )
(6)如果一数列满足 ,那么该数列为递增数列. ( )
答案:(1)× (2)× (3)√ (4)√ (5)√ (6)×探究一探究二探究三探究四探究五思维辨析数列的概念
【例1】 下列叙述正确的是( )
A.数列2,4,6,8和数列4,2,6,8是同一个数列
B.同一个数在数列中可能重复出现
C.数列的通项公式是定义域为正整数集N+的函数
D.数列的通项公式是唯一的
解析:根据数列的定义,如果组成两个数列的数相同而排列次序不同,那么它们就是不同的数列,因此,A是错误的;数列的通项公式的定义域是正整数集N+或它的有限子集,因此,C是错误的;数列-1,1,-1,1,-1,1,…的通项公式可以写成an=(-1)n,也可以写成an=(-1)n+2,还可以写成分段函数的形式,因此,D是错误的;而数列中的数可以重复出现,故选B.
答案:B当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟运用数列的定义判断一组元素是否为数列的一般步骤是:(1)判断这组元素是否都是数;(2)判断这组元素是否按照一定的顺序排列.注意:按一定顺序不表示该数列具有规律性,即数列中的每一项可以是有规律的,也可以是无规律的.当堂检测探究一探究二探究三探究四探究五思维辨析根据通项公式求项
【例2】 根据下面数列的通项公式,写出它们的前5项.思路分析:已知数列的通项公式,依次用1,2,3,…代替公式中的n,便可以求出数列的各项.(2)在通项公式an=3n+2n中,依次取n=1,2,3,4,5,得到数列的前5项分别为a1=3×1+21=5,a2=3×2+22=10,a3=3×3+23=17, a4=3×4+24=28,a5=3×5+25=47.当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,便可以求出相应的各项,实际上相当于已知函数的定义域和解析式,求函数值.当堂检测探究一探究二探究三探究四探究五思维辨析由数列的前n项写出其通项公式 当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟1.根据数列的前几项写对应的通项公式的一般思路是:
(1)先统一项的结构,如都化成分数、根式等;
(2)分析这一结构中变化的部分与不变的部分,探索变化部分的变化规律与对应序号间的函数关系式;
(3)对于符号交替出现的情况,可先观察其绝对值,再以(-1)k处理符号;
(4)对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.当堂检测探究一探究二探究三探究四探究五思维辨析2.常见数列的通项公式如下:
(1)数列-1,1,-1,1,…的通项公式是an=(-1)n;
(2)数列1,2,3,4,…的通项公式是an=n;
(3)数列1,3,5,7,…的通项公式是an=2n-1;
(4)数列2,4,6,8,…的通项公式是an=2n;
(5)数列1,2,4,8,…的通项公式是an=2n-1;
(6)数列1,4,9,16,…的通项公式是an=n2;当堂检测探究一探究二探究三探究四探究五思维辨析(1)将本例3(2)④中的数列变为1,11,111,1 111,…结果如何?
(2)变为5,55,555,5 555,…结果又如何?当堂检测探究一探究二探究三探究四判断数列的单调性
【例4】已知函数f(x)= .数列{an}满足f(an)=-2n,且an>0.
(1)求数列{an}的通项公式;
(2)判断数列{an}的增减性.
思路分析:先根据已知条件解方程求an,再利用作差法或作商法判断数列{an}的增减性.探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟数列增减性的判定方法
1.作差比较法
(1)若an+1-an>0恒成立,则数列{an}是递增数列;
(2)若an+1-an<0恒成立,则数列{an}是递减数列;
(3)若an+1-an=0恒成立,则数列{an}是常数列.
2.作商比较法当堂检测探究一探究二探究三探究四变式训练1若数列{an}满足an=-n2+2n+9(n∈N+),则该数列是
数列.(填“递增”“递减”或“摆动”)?
答案:递减探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测数列与函数的关系
【例5】 已知数列{an}的通项公式是 ,试问该数列{an}有没有最大项?若有,求出最大项和最大项的序号;若没有,请说明理由.
思路分析:探求数列的最大项可以通过作差或不等式组解决.探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测反思感悟1.数列是一种特殊的函数,因此在解决数列问题时,要善于利用函数的知识、函数的观点、函数的思想方法来解题.
2.根据数列的特殊性,由于它的定义域是N+或它的有限子集{1,2,…,n},因而它的图象是一系列孤立的点,而不像我们前面所研究过的初等函数一般都是连续的曲线.
3.利用数列(函数)的单调性可以求数列中的最大(最小)项.
一般常用方法为:探究一探究二探究三探究四探究五思维辨析当堂检测变式训练2数列{-2n2+29n+3}中的最大项为 .?
解析:由已知得an=-2n2+29n+3=
∵n∈N+,∴当n=7时,an取得最大值,即a7=108.
答案:108探究一探究二探究三探究四探究五思维辨析当堂检测因未考虑到数列是一种特殊的函数而致误
【典例】 已知在数列{an}中,an=n2-kn(n∈N+),且{an}单调递增,则k的取值范围是( )
A.(-∞,2] B.(-∞,3)
C.(-∞,2) D.(-∞,3]
错解因为an是关于n的二次函数,其定义域为正整数集,故若{an}递增,则必有 ≤1,故k≤2.故选A.
正解an+1-an=(n+1)2-k(n+1)-n2+kn=2n+1-k.由于{an}单调递增,故应有an+1-an>0,即2n+1-k>0恒成立,所以k<2n+1,故只需k<3即可.故选B.
答案:B探究一探究二探究三探究四探究五思维辨析当堂检测纠错心得函数的单调性与数列的单调性既有联系又有区别,即数列所对应的函数若单调,则数列一定单调,反之若数列单调,其所对应的函数不一定单调.关键原因在于数列是一个定义域为正整数集N+(或它的有限子集{1,2,3,…,n})的特殊函数,故对于数列的单调性的判断一般要通过比较an+1与an的大小来判断:若an+1>an,则数列为递增数列;若an+1A.λ>0 B.λ<0
C.λ≥-2 D.λ>-3
解析:由题意知an+1>an,
则(n+1)2+λ(n+1)>n2+λn,即λ>-2n-1.
∵n≥1,∴λ>-3.故选D.
答案:D探究一探究二探究三探究四探究五思维辨析当堂检测1.以下四个数中,哪个数是数列{n(n+1)}中的一项( )
A.380 B.39 C.32 D.23
解析:n(n+1)是这个数列的通项公式,即an=n(n+1).
∵380=19×20=19×(19+1),∴380是该数列中的第19项,或者令n(n+1)=380,得n=19,是整数,符合题意.故选A.
答案:A
2.在数列1,1,2,3,5,8,13,x,34,…中,x的值是( )
A.19 B.20 C.21 D.22
解析:观察数列可得规律:1+1=2,1+2=3,2+3=5,……8+13=x=21, 13+21=34,
∴x=21,故选C.
答案:C探究一探究二探究三探究四探究五思维辨析当堂检测答案:D 探究一探究二探究三探究四探究五思维辨析当堂检测答案:14 探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测
【问题思考】
1.填空:
(1)数列的定义:按照一定次序排列起来的一列数叫做数列,数列中的每一个数都叫做这个数列的项.
(2)数列的一般形式可以写成a1,a2,a3,…,an,….其中an是数列的第n项,叫做数列的通项,一般形式的数列简记作{an},这里{an}是数列的简记符号,并不表示一个集合.
2.数列2,3,4,5,6与集合{2,3,4,5,6}有何区别?
提示:数列2,3,4,5,6是按一定的次序排列的,打乱顺序后又产生新的数列;而{2,3,4,5,6}中元素无论按怎样的顺序排列都是同一个集合.一二三四二、数列的通项公式
【问题思考】
1.填空:
如果数列{an}的第n项an与n之间的关系可以用一个函数式an=f(n)来表示,那么这个公式就叫做这个数列的通项公式.一二三四一二三四三、数列与函数的关系
【问题思考】
1.填空:
在数列{an}中,对于每一个正整数n(或n∈{1,2,…,k}),都有一个数an与之对应,因此,数列可以看成以正整数N+(或它的有限子集{1,2,…,k})为定义域的函数an=f(n),即当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.反过来,对于函数y=f(x),如果f(i)(i=1,2,3,…)有意义,那么我们可以得到一个数列f(1),f(2),f(3),…,f(n),…,其图象是一系列孤立的点.一二三四2.数列{an}与函数f(n)=an(n∈N+)的区别如何?
提示:(1)数列{an}与函数f(n)=an(n∈N+)是不同的,{an}中的元素具有有序性,如将a1,a2,a3,…,an排成a3,a1,a2,…,an,则为不同的数列,而对于函数f(n)=an(n∈N+)来说却是一样的.
(2)数列中,自变量的取值更有规律性,必须从小到大取正整数.
3.做一做:已知数列{an}的通项公式为an=n2-8n+15,则( )
A.3不是数列{an}中的项
B.3只是数列{an}中的第2项
C.3只是数列{an}中的第6项
D.3是数列{an}中的第2项或第6项
解析:令an=3,即n2-8n+15=3,解得n=2或n=6.
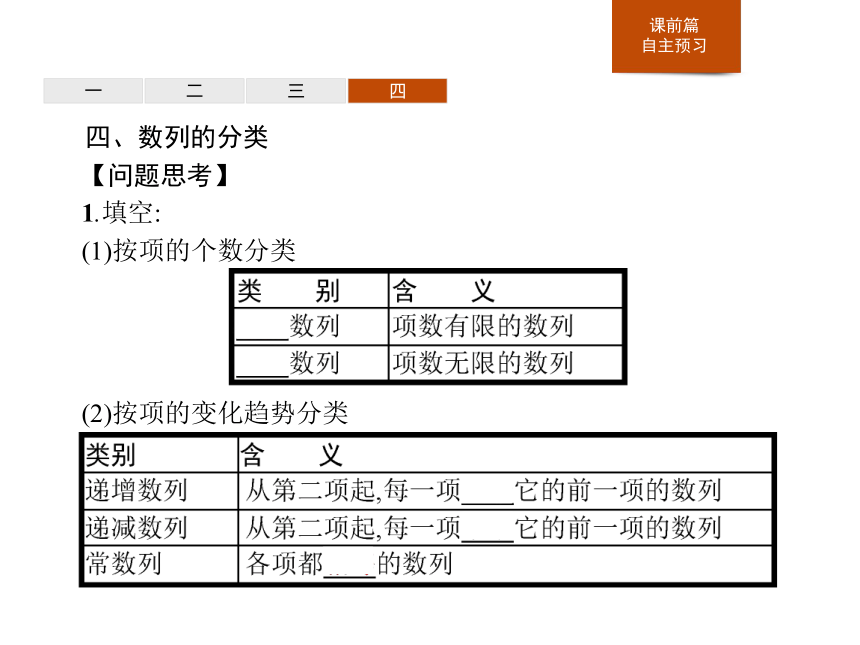
答案:D一二三四四、数列的分类
【问题思考】
1.填空:
(1)按项的个数分类(2)按项的变化趋势分类 一二三四2.是否存在一个各项都小于5的无穷递增数列?如果存在,请写出一个这样的数列的通项公式.3.做一做:已知下列数列:
①-1,0,1,2,3,4,…,n.
②1,-1,1,-1,….④6,6,6,6,6.
其中递增数列有 ,递减数列有 ,常数列有 ,有穷数列有 ,无穷数列有 (只填序号就可以).?
答案:① ③ ④ ①④ ②③一二三四思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)数列是按一定顺序排列的有规律的一列数. ( )
(2)数列中的项不可能相等. ( )
(3)数列是可以用图象表示的. ( )
(4)数列可以用一群孤立的点表示. ( )
(5)数列可以看成一种特殊的函数. ( )
(6)如果一数列满足 ,那么该数列为递增数列. ( )
答案:(1)× (2)× (3)√ (4)√ (5)√ (6)×探究一探究二探究三探究四探究五思维辨析数列的概念
【例1】 下列叙述正确的是( )
A.数列2,4,6,8和数列4,2,6,8是同一个数列
B.同一个数在数列中可能重复出现
C.数列的通项公式是定义域为正整数集N+的函数
D.数列的通项公式是唯一的
解析:根据数列的定义,如果组成两个数列的数相同而排列次序不同,那么它们就是不同的数列,因此,A是错误的;数列的通项公式的定义域是正整数集N+或它的有限子集,因此,C是错误的;数列-1,1,-1,1,-1,1,…的通项公式可以写成an=(-1)n,也可以写成an=(-1)n+2,还可以写成分段函数的形式,因此,D是错误的;而数列中的数可以重复出现,故选B.
答案:B当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟运用数列的定义判断一组元素是否为数列的一般步骤是:(1)判断这组元素是否都是数;(2)判断这组元素是否按照一定的顺序排列.注意:按一定顺序不表示该数列具有规律性,即数列中的每一项可以是有规律的,也可以是无规律的.当堂检测探究一探究二探究三探究四探究五思维辨析根据通项公式求项
【例2】 根据下面数列的通项公式,写出它们的前5项.思路分析:已知数列的通项公式,依次用1,2,3,…代替公式中的n,便可以求出数列的各项.(2)在通项公式an=3n+2n中,依次取n=1,2,3,4,5,得到数列的前5项分别为a1=3×1+21=5,a2=3×2+22=10,a3=3×3+23=17, a4=3×4+24=28,a5=3×5+25=47.当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,便可以求出相应的各项,实际上相当于已知函数的定义域和解析式,求函数值.当堂检测探究一探究二探究三探究四探究五思维辨析由数列的前n项写出其通项公式 当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟1.根据数列的前几项写对应的通项公式的一般思路是:
(1)先统一项的结构,如都化成分数、根式等;
(2)分析这一结构中变化的部分与不变的部分,探索变化部分的变化规律与对应序号间的函数关系式;
(3)对于符号交替出现的情况,可先观察其绝对值,再以(-1)k处理符号;
(4)对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.当堂检测探究一探究二探究三探究四探究五思维辨析2.常见数列的通项公式如下:
(1)数列-1,1,-1,1,…的通项公式是an=(-1)n;
(2)数列1,2,3,4,…的通项公式是an=n;
(3)数列1,3,5,7,…的通项公式是an=2n-1;
(4)数列2,4,6,8,…的通项公式是an=2n;
(5)数列1,2,4,8,…的通项公式是an=2n-1;
(6)数列1,4,9,16,…的通项公式是an=n2;当堂检测探究一探究二探究三探究四探究五思维辨析(1)将本例3(2)④中的数列变为1,11,111,1 111,…结果如何?
(2)变为5,55,555,5 555,…结果又如何?当堂检测探究一探究二探究三探究四判断数列的单调性
【例4】已知函数f(x)= .数列{an}满足f(an)=-2n,且an>0.
(1)求数列{an}的通项公式;
(2)判断数列{an}的增减性.
思路分析:先根据已知条件解方程求an,再利用作差法或作商法判断数列{an}的增减性.探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析反思感悟数列增减性的判定方法
1.作差比较法
(1)若an+1-an>0恒成立,则数列{an}是递增数列;
(2)若an+1-an<0恒成立,则数列{an}是递减数列;
(3)若an+1-an=0恒成立,则数列{an}是常数列.
2.作商比较法当堂检测探究一探究二探究三探究四变式训练1若数列{an}满足an=-n2+2n+9(n∈N+),则该数列是
数列.(填“递增”“递减”或“摆动”)?
答案:递减探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测数列与函数的关系
【例5】 已知数列{an}的通项公式是 ,试问该数列{an}有没有最大项?若有,求出最大项和最大项的序号;若没有,请说明理由.
思路分析:探求数列的最大项可以通过作差或不等式组解决.探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测反思感悟1.数列是一种特殊的函数,因此在解决数列问题时,要善于利用函数的知识、函数的观点、函数的思想方法来解题.
2.根据数列的特殊性,由于它的定义域是N+或它的有限子集{1,2,…,n},因而它的图象是一系列孤立的点,而不像我们前面所研究过的初等函数一般都是连续的曲线.
3.利用数列(函数)的单调性可以求数列中的最大(最小)项.
一般常用方法为:探究一探究二探究三探究四探究五思维辨析当堂检测变式训练2数列{-2n2+29n+3}中的最大项为 .?
解析:由已知得an=-2n2+29n+3=
∵n∈N+,∴当n=7时,an取得最大值,即a7=108.
答案:108探究一探究二探究三探究四探究五思维辨析当堂检测因未考虑到数列是一种特殊的函数而致误
【典例】 已知在数列{an}中,an=n2-kn(n∈N+),且{an}单调递增,则k的取值范围是( )
A.(-∞,2] B.(-∞,3)
C.(-∞,2) D.(-∞,3]
错解因为an是关于n的二次函数,其定义域为正整数集,故若{an}递增,则必有 ≤1,故k≤2.故选A.
正解an+1-an=(n+1)2-k(n+1)-n2+kn=2n+1-k.由于{an}单调递增,故应有an+1-an>0,即2n+1-k>0恒成立,所以k<2n+1,故只需k<3即可.故选B.
答案:B探究一探究二探究三探究四探究五思维辨析当堂检测纠错心得函数的单调性与数列的单调性既有联系又有区别,即数列所对应的函数若单调,则数列一定单调,反之若数列单调,其所对应的函数不一定单调.关键原因在于数列是一个定义域为正整数集N+(或它的有限子集{1,2,3,…,n})的特殊函数,故对于数列的单调性的判断一般要通过比较an+1与an的大小来判断:若an+1>an,则数列为递增数列;若an+1
C.λ≥-2 D.λ>-3
解析:由题意知an+1>an,
则(n+1)2+λ(n+1)>n2+λn,即λ>-2n-1.
∵n≥1,∴λ>-3.故选D.
答案:D探究一探究二探究三探究四探究五思维辨析当堂检测1.以下四个数中,哪个数是数列{n(n+1)}中的一项( )
A.380 B.39 C.32 D.23
解析:n(n+1)是这个数列的通项公式,即an=n(n+1).
∵380=19×20=19×(19+1),∴380是该数列中的第19项,或者令n(n+1)=380,得n=19,是整数,符合题意.故选A.
答案:A
2.在数列1,1,2,3,5,8,13,x,34,…中,x的值是( )
A.19 B.20 C.21 D.22
解析:观察数列可得规律:1+1=2,1+2=3,2+3=5,……8+13=x=21, 13+21=34,
∴x=21,故选C.
答案:C探究一探究二探究三探究四探究五思维辨析当堂检测答案:D 探究一探究二探究三探究四探究五思维辨析当堂检测答案:14 探究一探究二探究三探究四探究五思维辨析当堂检测探究一探究二探究三探究四探究五思维辨析当堂检测
