3.4 不等式的实际应用:27张PPT
文档属性
| 名称 | 3.4 不等式的实际应用:27张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 619.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
3.4 不等式的实际应用
一
二
一
二
二、不等式解决实际问题的步骤
【问题思考】
1.填空:
(1)设未知数:用字母表示题中的未知数.
(2)列不等式(组):找出题中的不等量关系,列出关于未知数的不等式(组).
(3)解不等式(组):运用不等式知识求解不等式,同时要注意未知数在实际问题中的取值范围.
(4)答:规范地写出答案.
一
二
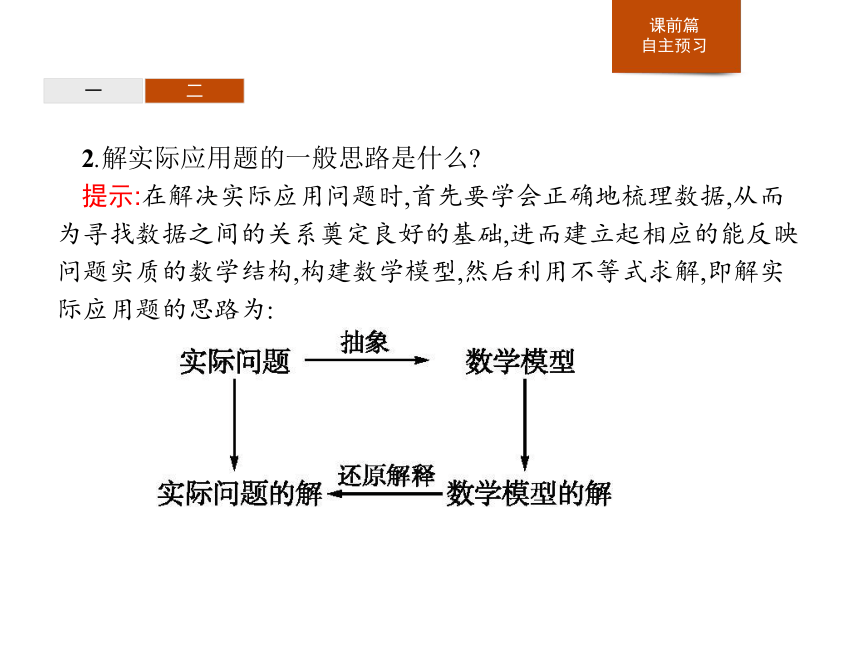
2.解实际应用题的一般思路是什么
提示:在解决实际应用问题时,首先要学会正确地梳理数据,从而为寻找数据之间的关系奠定良好的基础,进而建立起相应的能反映问题实质的数学结构,构建数学模型,然后利用不等式求解,即解实际应用题的思路为:
一
二
3.做一做:用两种金属材料做一个矩形框架,按要求长和宽应选用的金属材料价格每1 m分别为3元和5元,且长和宽必须是整数,现预算花费不超过100元,则做成矩形框架围成的最大面积是 .
答案:40 m2
一
二
思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(3)一艘轮船在匀速行驶过程中每小时的燃料费与它速度的平方成正比,除燃料费外其他费用为每小时96元.当速度为10海里/时时,每小时的燃料费是6元.若匀速行驶10海里,则当这艘轮船以40海里/时的速度航行时,费用总和取得最小值. ( )
答案:(1)√ (2)× (3)√
探究一
探究二
思维辨析
当堂检测
一元二次不等式的实际应用
【例1】 某农贸公司按每担200元收购某农产品,并且每100元需纳税10元(又称征税率为10个百分点),计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x≠0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
探究一
探究二
思维辨析
当堂检测
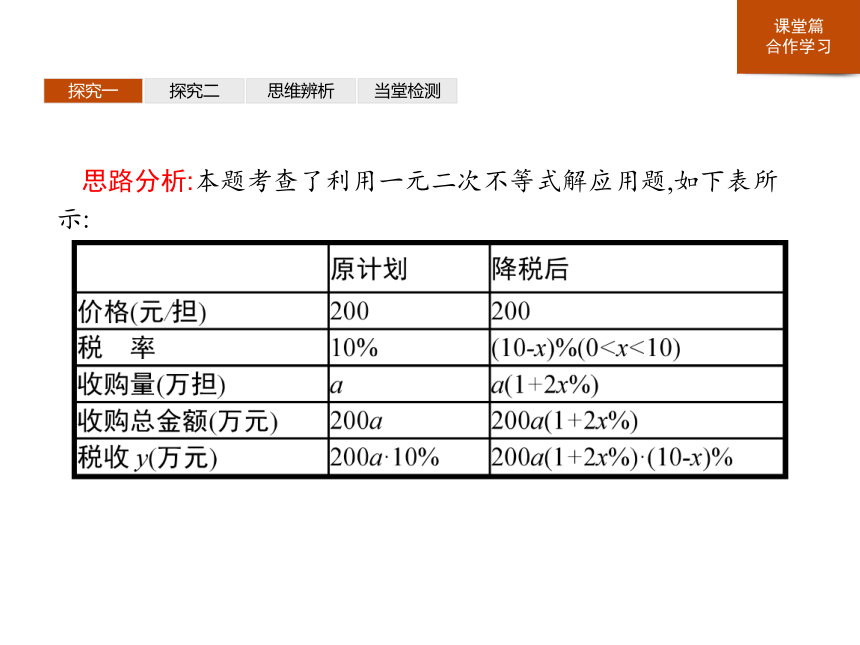
思路分析:本题考查了利用一元二次不等式解应用题,如下表所示:
探究一
探究二
思维辨析
当堂检测
解:(1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.
化简,得x2+40x-84≤0,
解得-42≤x≤2.
又∵0∴x的取值范围为(0,2].
反思感悟解决此类实际问题的关键是先仔细阅读题目,弄清题中复杂的变量关系,再提炼出一元二次不等式的数学模型,列表法能比较清晰地反映各个量之间的关系.最后要将所得数学问题的解回归到实际问题中.
探究一
探究二
思维辨析
当堂检测
变式训练1某企业生产一种产品x(百件)的成本为(3x-3)万元,销售总收入为(2x2-5)万元,如果要保证该企业不亏本,那么至少生产该产品为 (百件).
解析:要不亏本只需收入不小于成本,即2x2-5-(3x-3)≥0,即2x2-3x-2≥0,解得x≤- 或x≥2,而产品件数不能是负数,所以x的最小值为2.
答案:2
探究一
探究二
思维辨析
当堂检测
利用均值不等式解实际应用题
【例2】 某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限1人,每天只限1次,某班有48名同学,老师打算组织同学们集体去游泳,除需要购买游泳卡外,每次还要包1辆车,无论乘坐多少名乘客,包车费均为40元,若使每位同学游泳8次,每人需至少交多少钱
思路分析:可从需购买若干张游泳卡或分若干批去游泳两个出发点考虑.
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
反思感悟应用均值不等式解决实际问题的方法与步骤
1.先理解题意,设变量.设变量时一般把要求最大值或最小值的变量定为函数;
2.建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
3.在定义域内,求出函数的最大值或最小值;
4.写出正确答案.
探究一
探究二
思维辨析
当堂检测
变式训练2某厂家拟在2018年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x(万件)与年促销费用m(万元)(m≥0)满足 (k为常数).如果不举行促销活动,那么该产品的年销售量只能是1万件.已知2018年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每年产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2018年该产品的利润y(万元)表示为年促销费用m(万元)的函数.
(2)该厂家2018年的促销费用投入多少万元时,厂家的利润最大 并求出最大利润.
探究一
探究二
思维辨析
当堂检测
解:(1)由题意,知当m=0时,x=1,
探究一
探究二
思维辨析
当堂检测
因未进行分类讨论而致误
【典例】 甲、乙两地水路相距s km,一条船由甲地逆流匀速行驶至乙地,水流速度为常量p km/h,船在静水中的最大速度为q km/h (q>p).已知船每小时的燃料费用(元)与船在静水中的速度v(km/h)的平方成正比,比例系数为k.
(1)把全程燃料费用y(元)表示为船在静水中的速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程燃料费用最少,船的实际前进速度应是多少
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
正解(1)同错解(1).
(2)解题过程同错解(2).
若2p≤q,则当v=2p时,y取最小值,
这时船的实际前进速度为p km/h.
若2p>q,当v∈(p,q]时,
探究一
探究二
思维辨析
当堂检测
纠错心得1.利用均值不等式来解决函数的最值或值域问题时,一定要弄清从实际问题中抽象出函数模型的结构形式及其定义域,若不具备运用均值不等式的形式,则可考虑能否先变形再应用.另一个重要问题是使用均值不等式时一定要注意能否取得等号,如果不能取得等号,那么可考虑用函数的单调性处理.
2.对于本题而言,显然通过变形可以运用均值不等式,但由于不知道2p与q的大小关系,因此需要分2p≤q和2p>q两种情况进行讨论.
探究一
探究二
思维辨析
当堂检测
1.某居民小区收取冬季供暖费,根据规定,住户可以从以下两种方案中任选其一:(1)按照使用面积缴纳,每平方米22元;(2)按照建筑面积缴纳,每平方米15元.李明家的使用面积是60平方米.如果他家选择第(2)种方案缴纳的供暖费不多于按第(1)种方案缴纳的供暖费,那么他家的建筑面积最多不超过( )
A.70平方米 B.88平方米
C.90平方米 D.100平方米
解析:根据使用面积应该缴纳的费用为60×22=1 320元,设建筑面积为x平方米,则根据他所选择的方案,知15x≤1 320,所以x≤88,即建筑面积不超过88平方米.
答案:B
探究一
探究二
思维辨析
当堂检测
2.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
答案:A
探究一
探究二
思维辨析
当堂检测
3.一个人以6 m/s的匀速度追赶停在交通灯前的汽车,当他离汽车25 m时交通灯由红变绿,汽车开始做变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的速度为v(t)=t m/s,则此人( )
A.可在7 s内追上汽车
B.可在9 s内追上汽车
C.不能追上汽车,但其间最近距离为14 m
D.不能追上汽车,但其间最近距离为7 m
答案:D
探究一
探究二
思维辨析
当堂检测
4.某种汽车,购车费用是10万元,每年使用的保险费、养路费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元.问这种汽车使用多少年时,它的年平均费用最少
分析:每年的保险费、养路费等是一个定数,关键是每年的维修费逐年递增,构成一个等差数列,只需求出x年的总费用(包括购车费)除以x年,即为平均费用y.列出函数关系式,再求解.
探究一
探究二
思维辨析
当堂检测
解:设汽车使用的年数为x.
由于“年维修费第一年是0.2万元,以后逐年递增0.2万元”,可知汽车每年维修费构成以0.2万元为首项,0.2万元为公差的等差数列.
探究一
探究二
思维辨析
当堂检测
5.某企业上年度的年利润为200万元,本年度为适应市场需求,计划提高产品档次,适度增加投入成本,投入成本增加的比例为x(0解:f(x)-g(x)=(-20x2+60x+200)-(-30x2+65x+200)=10x2-5x.
3.4 不等式的实际应用
一
二
一
二
二、不等式解决实际问题的步骤
【问题思考】
1.填空:
(1)设未知数:用字母表示题中的未知数.
(2)列不等式(组):找出题中的不等量关系,列出关于未知数的不等式(组).
(3)解不等式(组):运用不等式知识求解不等式,同时要注意未知数在实际问题中的取值范围.
(4)答:规范地写出答案.
一
二
2.解实际应用题的一般思路是什么
提示:在解决实际应用问题时,首先要学会正确地梳理数据,从而为寻找数据之间的关系奠定良好的基础,进而建立起相应的能反映问题实质的数学结构,构建数学模型,然后利用不等式求解,即解实际应用题的思路为:
一
二
3.做一做:用两种金属材料做一个矩形框架,按要求长和宽应选用的金属材料价格每1 m分别为3元和5元,且长和宽必须是整数,现预算花费不超过100元,则做成矩形框架围成的最大面积是 .
答案:40 m2
一
二
思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(3)一艘轮船在匀速行驶过程中每小时的燃料费与它速度的平方成正比,除燃料费外其他费用为每小时96元.当速度为10海里/时时,每小时的燃料费是6元.若匀速行驶10海里,则当这艘轮船以40海里/时的速度航行时,费用总和取得最小值. ( )
答案:(1)√ (2)× (3)√
探究一
探究二
思维辨析
当堂检测
一元二次不等式的实际应用
【例1】 某农贸公司按每担200元收购某农产品,并且每100元需纳税10元(又称征税率为10个百分点),计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x≠0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
探究一
探究二
思维辨析
当堂检测
思路分析:本题考查了利用一元二次不等式解应用题,如下表所示:
探究一
探究二
思维辨析
当堂检测
解:(1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.
化简,得x2+40x-84≤0,
解得-42≤x≤2.
又∵0
反思感悟解决此类实际问题的关键是先仔细阅读题目,弄清题中复杂的变量关系,再提炼出一元二次不等式的数学模型,列表法能比较清晰地反映各个量之间的关系.最后要将所得数学问题的解回归到实际问题中.
探究一
探究二
思维辨析
当堂检测
变式训练1某企业生产一种产品x(百件)的成本为(3x-3)万元,销售总收入为(2x2-5)万元,如果要保证该企业不亏本,那么至少生产该产品为 (百件).
解析:要不亏本只需收入不小于成本,即2x2-5-(3x-3)≥0,即2x2-3x-2≥0,解得x≤- 或x≥2,而产品件数不能是负数,所以x的最小值为2.
答案:2
探究一
探究二
思维辨析
当堂检测
利用均值不等式解实际应用题
【例2】 某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限1人,每天只限1次,某班有48名同学,老师打算组织同学们集体去游泳,除需要购买游泳卡外,每次还要包1辆车,无论乘坐多少名乘客,包车费均为40元,若使每位同学游泳8次,每人需至少交多少钱
思路分析:可从需购买若干张游泳卡或分若干批去游泳两个出发点考虑.
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
反思感悟应用均值不等式解决实际问题的方法与步骤
1.先理解题意,设变量.设变量时一般把要求最大值或最小值的变量定为函数;
2.建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
3.在定义域内,求出函数的最大值或最小值;
4.写出正确答案.
探究一
探究二
思维辨析
当堂检测
变式训练2某厂家拟在2018年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x(万件)与年促销费用m(万元)(m≥0)满足 (k为常数).如果不举行促销活动,那么该产品的年销售量只能是1万件.已知2018年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每年产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2018年该产品的利润y(万元)表示为年促销费用m(万元)的函数.
(2)该厂家2018年的促销费用投入多少万元时,厂家的利润最大 并求出最大利润.
探究一
探究二
思维辨析
当堂检测
解:(1)由题意,知当m=0时,x=1,
探究一
探究二
思维辨析
当堂检测
因未进行分类讨论而致误
【典例】 甲、乙两地水路相距s km,一条船由甲地逆流匀速行驶至乙地,水流速度为常量p km/h,船在静水中的最大速度为q km/h (q>p).已知船每小时的燃料费用(元)与船在静水中的速度v(km/h)的平方成正比,比例系数为k.
(1)把全程燃料费用y(元)表示为船在静水中的速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程燃料费用最少,船的实际前进速度应是多少
探究一
探究二
思维辨析
当堂检测
探究一
探究二
思维辨析
当堂检测
正解(1)同错解(1).
(2)解题过程同错解(2).
若2p≤q,则当v=2p时,y取最小值,
这时船的实际前进速度为p km/h.
若2p>q,当v∈(p,q]时,
探究一
探究二
思维辨析
当堂检测
纠错心得1.利用均值不等式来解决函数的最值或值域问题时,一定要弄清从实际问题中抽象出函数模型的结构形式及其定义域,若不具备运用均值不等式的形式,则可考虑能否先变形再应用.另一个重要问题是使用均值不等式时一定要注意能否取得等号,如果不能取得等号,那么可考虑用函数的单调性处理.
2.对于本题而言,显然通过变形可以运用均值不等式,但由于不知道2p与q的大小关系,因此需要分2p≤q和2p>q两种情况进行讨论.
探究一
探究二
思维辨析
当堂检测
1.某居民小区收取冬季供暖费,根据规定,住户可以从以下两种方案中任选其一:(1)按照使用面积缴纳,每平方米22元;(2)按照建筑面积缴纳,每平方米15元.李明家的使用面积是60平方米.如果他家选择第(2)种方案缴纳的供暖费不多于按第(1)种方案缴纳的供暖费,那么他家的建筑面积最多不超过( )
A.70平方米 B.88平方米
C.90平方米 D.100平方米
解析:根据使用面积应该缴纳的费用为60×22=1 320元,设建筑面积为x平方米,则根据他所选择的方案,知15x≤1 320,所以x≤88,即建筑面积不超过88平方米.
答案:B
探究一
探究二
思维辨析
当堂检测
2.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
答案:A
探究一
探究二
思维辨析
当堂检测
3.一个人以6 m/s的匀速度追赶停在交通灯前的汽车,当他离汽车25 m时交通灯由红变绿,汽车开始做变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的速度为v(t)=t m/s,则此人( )
A.可在7 s内追上汽车
B.可在9 s内追上汽车
C.不能追上汽车,但其间最近距离为14 m
D.不能追上汽车,但其间最近距离为7 m
答案:D
探究一
探究二
思维辨析
当堂检测
4.某种汽车,购车费用是10万元,每年使用的保险费、养路费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元.问这种汽车使用多少年时,它的年平均费用最少
分析:每年的保险费、养路费等是一个定数,关键是每年的维修费逐年递增,构成一个等差数列,只需求出x年的总费用(包括购车费)除以x年,即为平均费用y.列出函数关系式,再求解.
探究一
探究二
思维辨析
当堂检测
解:设汽车使用的年数为x.
由于“年维修费第一年是0.2万元,以后逐年递增0.2万元”,可知汽车每年维修费构成以0.2万元为首项,0.2万元为公差的等差数列.
探究一
探究二
思维辨析
当堂检测
5.某企业上年度的年利润为200万元,本年度为适应市场需求,计划提高产品档次,适度增加投入成本,投入成本增加的比例为x(0
