3.5.2 简单线性规划:42张PPT
文档属性
| 名称 | 3.5.2 简单线性规划:42张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-06 00:00:00 | ||
图片预览










文档简介
课件42张PPT。3.5.2 简单线性规划线性规划中的基本概念
【问题思考】
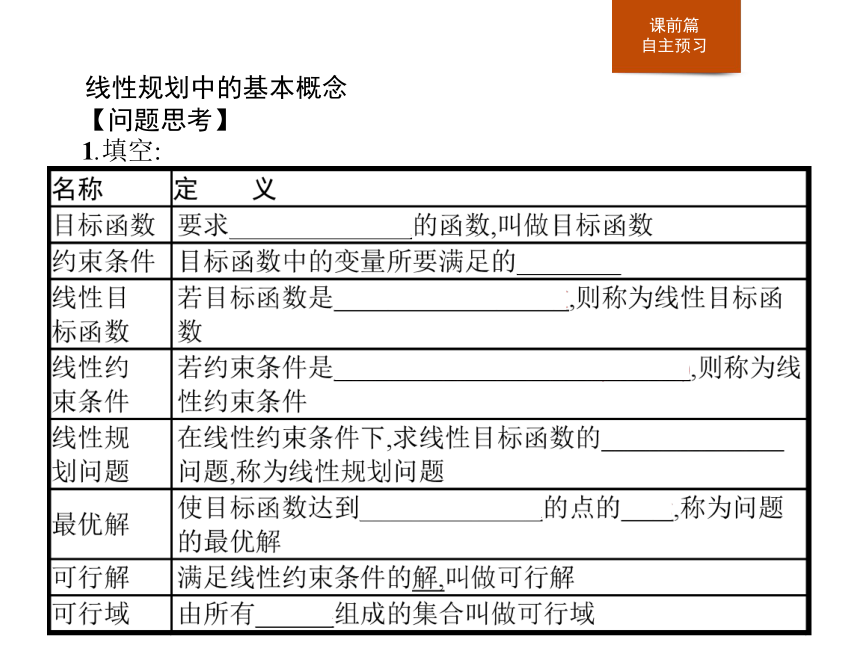
1.填空:2.可行解与最优解有何关系?最优解是否唯一?
提示:最优解必定是可行解,但可行解不一定是最优解,最优解有时唯一,有时有多个.
3.已知线性目标函数z=Ax+By+C(AB≠0),则系数B与z有什么内在联系?解析:画出可行域,寻找最优解.故找到(5,4)点,
得z=10x+10y的最大值为10×5+10×4=90.答案:C 知识链接线性规划问题的常见类型有:
(1)物资调运问题
例如已知A1,A2两煤矿每年的产量,煤需经B1,B2两个车站运往外地,B1,B2两车站的运输能力是有限的,且已知A1,A2两煤矿运往B1,B2两车站的运输价格,煤矿应怎样编制调运方案,能使总运费最少?
(2)产品安排问题
例如某工厂生产甲、乙两种产品,每生产一个单位的甲种或乙种产品所需A,B,C三种材料的数量、此厂每月所能提供的三种材料的限额、每生产一个单位甲种或乙种产品所获利润额都是已知的,这个厂每月应如何安排产品的生产,才能使每月获得的总利润最大?
(3)下料问题
例如要把一批长钢管截成两种规格的短钢管,怎样下料能使损耗最小?思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)若x,y满足线性约束条件,则目标函数z=Ax+By(B≠0)的最优解是唯一的. ( )
(2)目标函数z=Ax+By+C,当B<0时,z的值随直线在y轴上截距的增大而减小. ( )
(3)z=(x-a)2+(y-b)2型的目标函数表示的几何意义是可行域内的点(x,y)到点(a,b)的距离. ( )
答案:(1)× (2)√ (3)×探究一探究二探究三探究四当堂检测线性目标函数的最值问题 探究一探究二探究三探究四当堂检测解析:作出可行域如图中阴影部分所示. 答案:C 探究一探究二探究三探究四当堂检测反思感悟解决线性目标函数的最值问题一般用图解法.因此要求作图要准确、规范,且要弄清楚函数值与直线截距的内在联系.对于已知最值求参数这一逆向问题也同正向处理方式类似,需要自己先表示出目标函数的最值,再与已知提供的最值进行对应.探究一探究二探究三探究四当堂检测解析:线性目标函数z=2x-y满足的可行域如图所示.
?
将直线l0:y=2x平行移动,当直线l0经过点M(5,2)时,直线y=2x-z在y轴上的截距最小,也就是z取最大值,此时zmax=2×5-2=8.
答案:B探究一探究二探究三探究四当堂检测解:x+y的最小值与m无关,在(0,1)处取得;x+5y的最小值与m有关,这是由于x+3y-3=0与x-my+1=0的交点是与m有关的表达式.探究一探究二探究三探究四当堂检测非线性目标函数的最值问题 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测设d=(x+1)2+(y+1)2,则它表示可行域内的点到点(-1,-1)的距离的平方,以点(-1,-1)为圆心, 为半径画圆,当圆经过点B时,d最大;当圆经过点C时,d最小.
所以当x=3,y=4时,dmax=(3+1)2+(4+1)2=41;
当x=2,y=1时,dmin=(2+1)2+(1+1)2=13,
即(x+1)2+(y+1)2的最大值为41,最小值为13.
答案:(1)D (2)A (3)41 13探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测解: 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测简单的线性规划应用问题
【例3】 (2017天津高考,文16)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.探究一探究二探究三探究四当堂检测(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?探究一探究二探究三探究四当堂检测解:(1)由已知,x,y满足的数学关系式为 该二元一次不等式组所表示的平面区域为图1中的阴影部分: 图1 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测反思感悟简单线性规划应用问题的求解步骤
1.设:设出变量x,y,写出约束条件及目标函数.
2.作:作出可行域.
3.移:作一组平行直线l,平移l,找最优解.
4.解:联立方程组求最优解,并代入目标函数,求出最值.
5.答:写出答案.
总之:求解线性规划问题的基本程序是作可行域,画平行线,解方程组,求最值.探究一探究二探究三探究四当堂检测变式训练3某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米饭每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又使得费用最少?
分析:根据实际问题中的已知条件,找出约束条件和目标函数,再用图解法解之.先作可行域,再作出初始直线l0,通过向上或向下平移直线l0至可行域的边界点,便得最优解,再进一步求最值.探究一探究二探究三探究四当堂检测解:设每盒盒饭需要面食x(百克),米饭y(百克).
则所需费用为z=0.5x+0.4y,且x,y满足作出可行域,如图阴影部分所示. 令z=0,作直线l0:0.5x+0.4y=0,
即直线5x+4y=0.
由图形可知,把直线l0平移至过点A时,z取最小值.探究一探究二探究三探究四当堂检测最优整数解问题
【例4】某运输公司有7辆载重量为6 t的A型卡车与4辆载重量为10 t的B型卡车,有9名驾驶员,在建筑某高速公路中,该公司承包了每天至少搬运360 t土的任务.已知每辆往返的次数为:A型卡车8次,B型卡车6次;每辆卡车每天往返的成本费用情况:A型卡车160元,B型卡车252元.试问,A型卡车与B型卡车每天各出动多少辆时公司的成本费用最低?
思路分析:首先列出线性约束条件及目标函数,然后转化为线性规划问题.因为涉及该问题中卡车的数量均为整数,因此用“网格法”探求出可行域中的所有整点,再寻求最优解.探究一探究二探究三探究四当堂检测解:设每天出动的A型卡车数为x,则0≤x≤7;每天出动的B型卡车数为y,则0≤y≤4.因为每天出车的驾驶员最多9名,则x+y≤9,每天要完成的搬运任务为48x+60y≥360,每天公司所花成本费用为z=160x+252y.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测使l向上方平行移动,可发现它与上述的10个点最先接触到的点是P4(5,2),得到的z的值最小,zmin=160×5+252×2=1 304.
答:当公司每天出动A型卡车5辆,B型卡车2辆时,公司的成本费用最低.
反思感悟对于线性规划中的最优整数解问题,可先求出线性规划的最优解,若它是整数解,则问题解决;若不是,要在该非整数解周围可行域内寻求与之最近的整数解,可通过精确作图,打好网格的办法求得.探究一探究二探究三探究四当堂检测变式训练4某旅行社租用A,B两种型号的客车安排900名客人旅行,A,B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆,则租金最少为( )
A.31 200元 B.36 000元
C.36 800元 D.38 400元探究一探究二探究三探究四当堂检测答案:C 探究一探究二探究三探究四当堂检测解析:由题意画出可行域(如图). 答案:D 探究一探究二探究三探究四当堂检测解析:作出可行域如图中阴影部分,平移直线t=x-y,可得-1≤t≤2,故选C.答案:C 探究一探究二探究三探究四当堂检测解析: 答案:A 探究一探究二探究三探究四当堂检测4.某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为 万元.?探究一探究二探究三探究四当堂检测解析:设该企业每天生产甲、乙两种产品分别为x吨、y吨,
则利润z=3x+4y.答案:18 探究一探究二探究三探究四当堂检测解:作出可行域,如图阴影部分所示. 可求得A(1,3),B(3,1),C(7,9). 探究一探究二探究三探究四当堂检测
【问题思考】
1.填空:2.可行解与最优解有何关系?最优解是否唯一?
提示:最优解必定是可行解,但可行解不一定是最优解,最优解有时唯一,有时有多个.
3.已知线性目标函数z=Ax+By+C(AB≠0),则系数B与z有什么内在联系?解析:画出可行域,寻找最优解.故找到(5,4)点,
得z=10x+10y的最大值为10×5+10×4=90.答案:C 知识链接线性规划问题的常见类型有:
(1)物资调运问题
例如已知A1,A2两煤矿每年的产量,煤需经B1,B2两个车站运往外地,B1,B2两车站的运输能力是有限的,且已知A1,A2两煤矿运往B1,B2两车站的运输价格,煤矿应怎样编制调运方案,能使总运费最少?
(2)产品安排问题
例如某工厂生产甲、乙两种产品,每生产一个单位的甲种或乙种产品所需A,B,C三种材料的数量、此厂每月所能提供的三种材料的限额、每生产一个单位甲种或乙种产品所获利润额都是已知的,这个厂每月应如何安排产品的生产,才能使每月获得的总利润最大?
(3)下料问题
例如要把一批长钢管截成两种规格的短钢管,怎样下料能使损耗最小?思考辨析
判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
(1)若x,y满足线性约束条件,则目标函数z=Ax+By(B≠0)的最优解是唯一的. ( )
(2)目标函数z=Ax+By+C,当B<0时,z的值随直线在y轴上截距的增大而减小. ( )
(3)z=(x-a)2+(y-b)2型的目标函数表示的几何意义是可行域内的点(x,y)到点(a,b)的距离. ( )
答案:(1)× (2)√ (3)×探究一探究二探究三探究四当堂检测线性目标函数的最值问题 探究一探究二探究三探究四当堂检测解析:作出可行域如图中阴影部分所示. 答案:C 探究一探究二探究三探究四当堂检测反思感悟解决线性目标函数的最值问题一般用图解法.因此要求作图要准确、规范,且要弄清楚函数值与直线截距的内在联系.对于已知最值求参数这一逆向问题也同正向处理方式类似,需要自己先表示出目标函数的最值,再与已知提供的最值进行对应.探究一探究二探究三探究四当堂检测解析:线性目标函数z=2x-y满足的可行域如图所示.
?
将直线l0:y=2x平行移动,当直线l0经过点M(5,2)时,直线y=2x-z在y轴上的截距最小,也就是z取最大值,此时zmax=2×5-2=8.
答案:B探究一探究二探究三探究四当堂检测解:x+y的最小值与m无关,在(0,1)处取得;x+5y的最小值与m有关,这是由于x+3y-3=0与x-my+1=0的交点是与m有关的表达式.探究一探究二探究三探究四当堂检测非线性目标函数的最值问题 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测设d=(x+1)2+(y+1)2,则它表示可行域内的点到点(-1,-1)的距离的平方,以点(-1,-1)为圆心, 为半径画圆,当圆经过点B时,d最大;当圆经过点C时,d最小.
所以当x=3,y=4时,dmax=(3+1)2+(4+1)2=41;
当x=2,y=1时,dmin=(2+1)2+(1+1)2=13,
即(x+1)2+(y+1)2的最大值为41,最小值为13.
答案:(1)D (2)A (3)41 13探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测解: 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测简单的线性规划应用问题
【例3】 (2017天津高考,文16)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.探究一探究二探究三探究四当堂检测(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?探究一探究二探究三探究四当堂检测解:(1)由已知,x,y满足的数学关系式为 该二元一次不等式组所表示的平面区域为图1中的阴影部分: 图1 探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测反思感悟简单线性规划应用问题的求解步骤
1.设:设出变量x,y,写出约束条件及目标函数.
2.作:作出可行域.
3.移:作一组平行直线l,平移l,找最优解.
4.解:联立方程组求最优解,并代入目标函数,求出最值.
5.答:写出答案.
总之:求解线性规划问题的基本程序是作可行域,画平行线,解方程组,求最值.探究一探究二探究三探究四当堂检测变式训练3某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米饭每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又使得费用最少?
分析:根据实际问题中的已知条件,找出约束条件和目标函数,再用图解法解之.先作可行域,再作出初始直线l0,通过向上或向下平移直线l0至可行域的边界点,便得最优解,再进一步求最值.探究一探究二探究三探究四当堂检测解:设每盒盒饭需要面食x(百克),米饭y(百克).
则所需费用为z=0.5x+0.4y,且x,y满足作出可行域,如图阴影部分所示. 令z=0,作直线l0:0.5x+0.4y=0,
即直线5x+4y=0.
由图形可知,把直线l0平移至过点A时,z取最小值.探究一探究二探究三探究四当堂检测最优整数解问题
【例4】某运输公司有7辆载重量为6 t的A型卡车与4辆载重量为10 t的B型卡车,有9名驾驶员,在建筑某高速公路中,该公司承包了每天至少搬运360 t土的任务.已知每辆往返的次数为:A型卡车8次,B型卡车6次;每辆卡车每天往返的成本费用情况:A型卡车160元,B型卡车252元.试问,A型卡车与B型卡车每天各出动多少辆时公司的成本费用最低?
思路分析:首先列出线性约束条件及目标函数,然后转化为线性规划问题.因为涉及该问题中卡车的数量均为整数,因此用“网格法”探求出可行域中的所有整点,再寻求最优解.探究一探究二探究三探究四当堂检测解:设每天出动的A型卡车数为x,则0≤x≤7;每天出动的B型卡车数为y,则0≤y≤4.因为每天出车的驾驶员最多9名,则x+y≤9,每天要完成的搬运任务为48x+60y≥360,每天公司所花成本费用为z=160x+252y.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测使l向上方平行移动,可发现它与上述的10个点最先接触到的点是P4(5,2),得到的z的值最小,zmin=160×5+252×2=1 304.
答:当公司每天出动A型卡车5辆,B型卡车2辆时,公司的成本费用最低.
反思感悟对于线性规划中的最优整数解问题,可先求出线性规划的最优解,若它是整数解,则问题解决;若不是,要在该非整数解周围可行域内寻求与之最近的整数解,可通过精确作图,打好网格的办法求得.探究一探究二探究三探究四当堂检测变式训练4某旅行社租用A,B两种型号的客车安排900名客人旅行,A,B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆,则租金最少为( )
A.31 200元 B.36 000元
C.36 800元 D.38 400元探究一探究二探究三探究四当堂检测答案:C 探究一探究二探究三探究四当堂检测解析:由题意画出可行域(如图). 答案:D 探究一探究二探究三探究四当堂检测解析:作出可行域如图中阴影部分,平移直线t=x-y,可得-1≤t≤2,故选C.答案:C 探究一探究二探究三探究四当堂检测解析: 答案:A 探究一探究二探究三探究四当堂检测4.某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得的最大利润为 万元.?探究一探究二探究三探究四当堂检测解析:设该企业每天生产甲、乙两种产品分别为x吨、y吨,
则利润z=3x+4y.答案:18 探究一探究二探究三探究四当堂检测解:作出可行域,如图阴影部分所示. 可求得A(1,3),B(3,1),C(7,9). 探究一探究二探究三探究四当堂检测
