第1章 1.2 回归分析
图片预览










文档简介
课件37张PPT。§1.2 回归分析第一章 统计案例学习目标
1.会建立线性回归模型分析两个变量间的相关关系.
2.能通过相关系数判断两个变量间的线性相关程度.问题导学达标检测题型探究内容索引问题导学知识点一 回归分析及回归直线方程思考1 什么叫回归分析?
答案 回归分析是对具有相关关系的两个变量进行统计分析的一种方法.
思考2 回归分析中,利用回归直线方程求出的函数值一定是真实值吗?
答案 不一定是真实值,利用回归直线方程求的值,在很多时候是个预测值.梳理 (1)回归分析是对具有 的两个变量进行统计分析的一种常用方法.若两个变量之间具有线性相关关系,则称相应的回归分析为 .相关关系线性回归分析知识点二 相关系数1.对于变量x与Y随机抽到的n对数据(x1,y1),(x2,y2),…,(xn,yn),检验统计量是样本相关系数2.相关系数r的取值范围是 ,|r|越接近1,变量之间的线性相关程度越强;|r|越接近0,变量之间的线性相关程度越弱.当|r|>r0.05时,表明有95%的把握认为两个变量之间具有线性相关关系.[-1,1]1.求回归直线方程前可以不进行相关性检验.( )
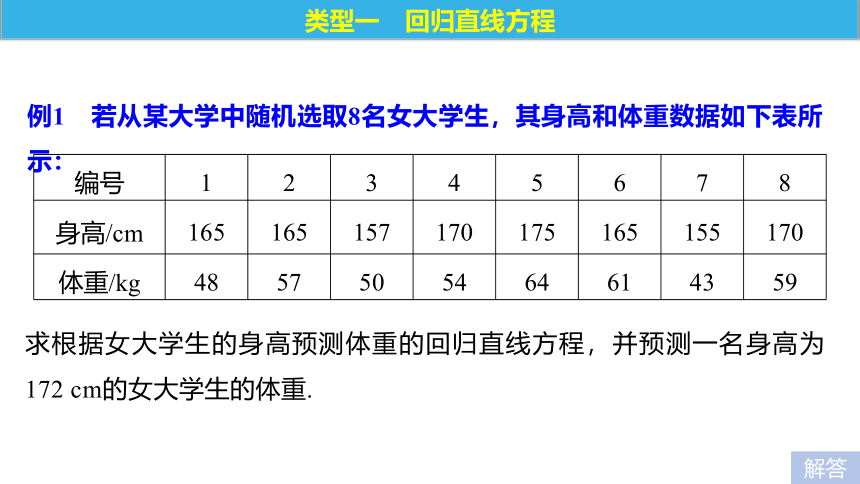
2.利用回归直线方程求出的值是准确值.( )[思考辨析 判断正误]××题型探究例1 若从某大学中随机选取8名女大学生,其身高和体重数据如下表所示:类型一 回归直线方程求根据女大学生的身高预测体重的回归直线方程,并预测一名身高为172 cm的女大学生的体重.解答解 (1)画散点图
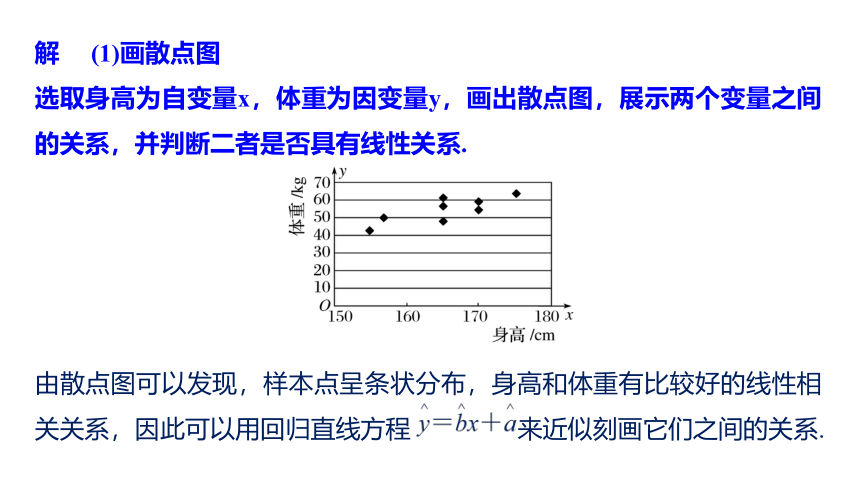
选取身高为自变量x,体重为因变量y,画出散点图,展示两个变量之间的关系,并判断二者是否具有线性关系.由散点图可以发现,样本点呈条状分布,身高和体重有比较好的线性相关关系,因此可以用回归直线方程 来近似刻画它们之间的关系.(3)预测和决策
即一名身高为172 cm的女大学生的体重预测值为60.224 kg.反思与感悟 在使用回归直线方程进行预测时要注意
(1)回归直线方程只适用于我们所研究的样本的总体.
(2)我们所建立的回归直线方程一般都有时间性.
(3)样本取值的范围会影响回归直线方程的适用范围.
(4)不能期望回归直线方程得到的预测值就是因变量的精确值.跟踪训练1 假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计数据:解答由此资料可知y对x呈线性相关关系.
(1)求回归直线方程;解 由题干表中的数据可得(2)求使用年限为10年时,该设备的维修费用为多少?解答即使用年限为10年时,该设备的维修费用约为12.38万元.例2 维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量,这个指标越高,耐热水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x(g/L)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据:类型二 相关性检验解答(1)画散点图;解 散点图如图.(2)求回归直线方程;解答(3)求相关系数r,并进行相关性检验.∵r=0.96>r0.05=0.754.
∴有95%的把握认为“甲醛浓度与缩醛化度有线性相关关系”,求得的回归直线方程有意义.解答反思与感悟 根据已知数据求得回归直线方程后,可以利用相关系数和临界值r0.05比较,进行相关性检验.跟踪训练2 为了研究3月下旬的平均气温(x)与4月20日前棉花害虫化蛹高峰日(y)的关系,某地区观察了2012年至2017年的情况,得到了下面的数据:解答(1)对变量x,y进行相关性检验;解 由已知条件可得下表:查表知:r0.05=0.811.由|r|>r0.05可知,变量y和x存在线性相关关系.(2)据气象预测,该地区在2019年3月下旬平均气温为27℃,试估计2019年4月化蛹高峰日为哪天.解答据此,可估计该地区2019年4月12日为化蛹高峰日.达标检测12341.某商品销售量y(件)与销售价格x(元/件)呈负相关,则其回归直线方程可能是答案√5解析 由于销售量y与销售价格x成负相关,故排除B,D.
又当x=10时,A中y=100,而C中y=-300,C不符合题意,故选A.解析2.下表是x和y之间的一组数据,则y关于x的回归直线必过
A.点(2,3) B.点(1.5,4)
C.点(2.5,4) D.点(2.5,5)解析答案√123453.对变量y和x进行相关性检验,已知n为数据的对数,r是相关系数,且已知①n=3,r=0.995 0;②n=7,r=0.953 3;③n=15,r=0.301 2;
④n=17,r=0.499 1.则变量y和x具有线性相关关系的是
A.①和② B.①和③
C.②和④ D.③和④解析答案√12345解析 ①当n=3时,r0.05=0.997,所以|r|②当n=7时,r0.05=0.754,所以|r|>r0.05,表明有95%的把握认为x与y之间具有线性相关关系;
③当n=15时,r0.05=0.514,所以|r|④当n=17时,r0.05=0.482,所以|r|>r0.05,表明有95%的把握认为x与y之间具有线性相关关系,所以②和④满足题意,故选C.123454.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:12345答案A.51个 B.50个 C.54个 D.48个√解析5.已知x,y之间的一组数据如下表:12345解答x1y1+x2y2+x3y3+x4y4=0×1+1×3+2×5+3×7=34,(2)已知变量x与y线性相关,求出回归直线方程.12345解答1.对具有线性相关关系的两个变量进行统计分析,可从散点图观察大致呈条状分布,可以求回归直线方程并进行预报.
2.通过求相关系数并和临界值r0.05比较可以判断两个变量是否有线性相关关系,求得的回归直线方程是否有意义.本课结束
1.会建立线性回归模型分析两个变量间的相关关系.
2.能通过相关系数判断两个变量间的线性相关程度.问题导学达标检测题型探究内容索引问题导学知识点一 回归分析及回归直线方程思考1 什么叫回归分析?
答案 回归分析是对具有相关关系的两个变量进行统计分析的一种方法.
思考2 回归分析中,利用回归直线方程求出的函数值一定是真实值吗?
答案 不一定是真实值,利用回归直线方程求的值,在很多时候是个预测值.梳理 (1)回归分析是对具有 的两个变量进行统计分析的一种常用方法.若两个变量之间具有线性相关关系,则称相应的回归分析为 .相关关系线性回归分析知识点二 相关系数1.对于变量x与Y随机抽到的n对数据(x1,y1),(x2,y2),…,(xn,yn),检验统计量是样本相关系数2.相关系数r的取值范围是 ,|r|越接近1,变量之间的线性相关程度越强;|r|越接近0,变量之间的线性相关程度越弱.当|r|>r0.05时,表明有95%的把握认为两个变量之间具有线性相关关系.[-1,1]1.求回归直线方程前可以不进行相关性检验.( )
2.利用回归直线方程求出的值是准确值.( )[思考辨析 判断正误]××题型探究例1 若从某大学中随机选取8名女大学生,其身高和体重数据如下表所示:类型一 回归直线方程求根据女大学生的身高预测体重的回归直线方程,并预测一名身高为172 cm的女大学生的体重.解答解 (1)画散点图
选取身高为自变量x,体重为因变量y,画出散点图,展示两个变量之间的关系,并判断二者是否具有线性关系.由散点图可以发现,样本点呈条状分布,身高和体重有比较好的线性相关关系,因此可以用回归直线方程 来近似刻画它们之间的关系.(3)预测和决策
即一名身高为172 cm的女大学生的体重预测值为60.224 kg.反思与感悟 在使用回归直线方程进行预测时要注意
(1)回归直线方程只适用于我们所研究的样本的总体.
(2)我们所建立的回归直线方程一般都有时间性.
(3)样本取值的范围会影响回归直线方程的适用范围.
(4)不能期望回归直线方程得到的预测值就是因变量的精确值.跟踪训练1 假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计数据:解答由此资料可知y对x呈线性相关关系.
(1)求回归直线方程;解 由题干表中的数据可得(2)求使用年限为10年时,该设备的维修费用为多少?解答即使用年限为10年时,该设备的维修费用约为12.38万元.例2 维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量,这个指标越高,耐热水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x(g/L)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据:类型二 相关性检验解答(1)画散点图;解 散点图如图.(2)求回归直线方程;解答(3)求相关系数r,并进行相关性检验.∵r=0.96>r0.05=0.754.
∴有95%的把握认为“甲醛浓度与缩醛化度有线性相关关系”,求得的回归直线方程有意义.解答反思与感悟 根据已知数据求得回归直线方程后,可以利用相关系数和临界值r0.05比较,进行相关性检验.跟踪训练2 为了研究3月下旬的平均气温(x)与4月20日前棉花害虫化蛹高峰日(y)的关系,某地区观察了2012年至2017年的情况,得到了下面的数据:解答(1)对变量x,y进行相关性检验;解 由已知条件可得下表:查表知:r0.05=0.811.由|r|>r0.05可知,变量y和x存在线性相关关系.(2)据气象预测,该地区在2019年3月下旬平均气温为27℃,试估计2019年4月化蛹高峰日为哪天.解答据此,可估计该地区2019年4月12日为化蛹高峰日.达标检测12341.某商品销售量y(件)与销售价格x(元/件)呈负相关,则其回归直线方程可能是答案√5解析 由于销售量y与销售价格x成负相关,故排除B,D.
又当x=10时,A中y=100,而C中y=-300,C不符合题意,故选A.解析2.下表是x和y之间的一组数据,则y关于x的回归直线必过
A.点(2,3) B.点(1.5,4)
C.点(2.5,4) D.点(2.5,5)解析答案√123453.对变量y和x进行相关性检验,已知n为数据的对数,r是相关系数,且已知①n=3,r=0.995 0;②n=7,r=0.953 3;③n=15,r=0.301 2;
④n=17,r=0.499 1.则变量y和x具有线性相关关系的是
A.①和② B.①和③
C.②和④ D.③和④解析答案√12345解析 ①当n=3时,r0.05=0.997,所以|r|
③当n=15时,r0.05=0.514,所以|r|
2.通过求相关系数并和临界值r0.05比较可以判断两个变量是否有线性相关关系,求得的回归直线方程是否有意义.本课结束
