第2章 2.1.1 合情推理
图片预览











文档简介
课件44张PPT。2.1.1 合情推理第二章 §2.1 合情推理与演绎推理学习目标
1.了解合情推理的含义,能利用归纳和类比等进行简单的推理.
2.了解合情推理在数学发现中的作用.问题导学达标检测题型探究内容索引问题导学知识点一 推理1.推理的概念与分类
(1)根据一个或几个 得出一个判断,这种思维方式就是推理.
(2)推理一般由两部分组成,一部分是已知的事实(或假设),叫做 ;一部分是由已知推出的判断,叫做 .
(3)推理一般分为 与 .
2.合情推理
前提为真时,结论 的推理,叫做合情推理.常用的合情推理有
和 .已知事实(或假设)前提结论合情推理演绎推理可能为真归纳推理类比推理知识点二 归纳推理思考 (1)铜、铁、铝、金、银等金属都能导电,猜想:一切金属都能导电.
(2)统计学中,从总体中抽取样本,然后用样本估计总体.
以上属于什么推理?答案 属于归纳推理.符合归纳推理的定义特征.梳理 归纳推理
(1)定义:根据一类事物的部分对象具有某种性质,推出这类事物的____
都具有这种性质的推理,叫做归纳推理(简称归纳),归纳是从___
到 的过程.
(2)归纳推理的一般步骤
①通过观察个别情况发现某些 .
②从已知的 中推出一个明确表述的 命题(猜想).所有对象特殊一般相同性质相同性质一般性知识点三 类比推理答案 类比推理.梳理 类比推理
(1)定义:根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另一类事物 的性质的推理,叫做类比推理(简称类比).
(2)类比推理的一般步骤
①找出两类事物之间的 或 .
②用一类事物的性质去推测另一类事物的性质,得出一个 的命题(猜想).类似(或相同)相似性一致性明确1.类比推理得到的结论可作为定理应用.( )
2.由个别到一般的推理为归纳推理.( )
3.在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.( )[思考辨析 判断正误]×√×题型探究命题角度1 数、式中的归纳推理
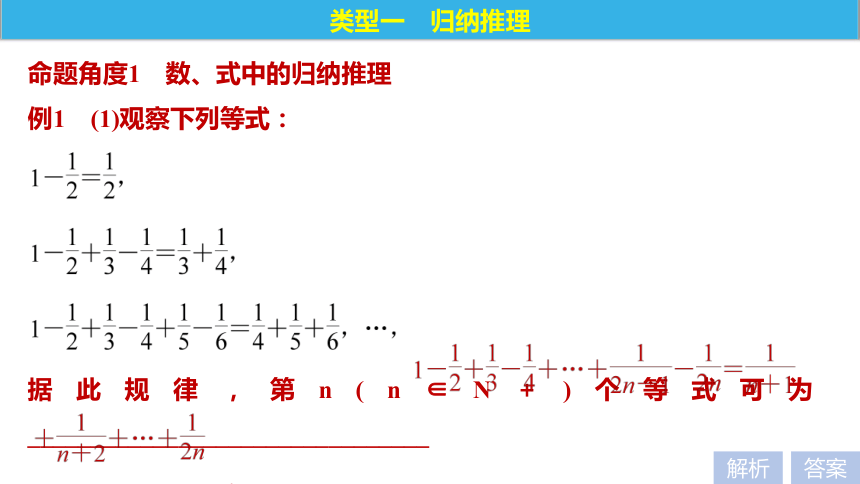
例1 (1)观察下列等式:
据此规律,第n(n∈N+)个等式可为________________________________
________________.类型一 归纳推理解析答案(2)已知f(x)= ,设f1(x)=f(x),fn(x)=fn-1(fn-1(x))(n>1,且n∈N+),
则f3(x)的表达式为_______________,猜想fn(x)(n∈N+)的表达式为________________.解析答案又∵fn(x)=fn-1(fn-1(x)),引申探究
在本例(2)中,若把“fn(x)=fn-1(fn-1(x))”改为“fn(x)=f(fn-1(x))”,其他条件不变,试猜想fn(x) (n∈N+)的表达式.解答又∵fn(x)=f(fn-1(x)),反思与感悟 (1)已知等式或不等式进行归纳推理的方法
①要特别注意所给几个等式(或不等式)中项数和次数等方面的变化规律;②要特别注意所给几个等式(或不等式)中结构形成的特征;③提炼出等式(或不等式)的综合特点;④运用归纳推理得出一般结论.
(2)数列中的归纳推理:在数列问题中,常常用到归纳推理猜测数列的通项公式或前n项和.
①通过已知条件求出数列的前几项或前n项和;②根据数列中的前几项或前n项和与对应序号之间的关系求解;③运用归纳推理写出数列的通项公式或前n项和公式.√答案解析(2)观察下列等式:答案解析命题角度2 几何中的归纳推理
例2 如图,第n个图形是由正n+2边形“扩展”而来(n=1,2,3,…),则第n个图形中顶点的个数为A.(n+1)(n+2) B.(n+2)(n+3)
C.n2 D.n√答案解析解析 由已知图形我们可以得到:
当n=1时,顶点共有12=3×4(个),
当n=2时,顶点共有20=4×5(个),
当n=3时,顶点共有30=5×6(个),
当n=4时,顶点共有42=6×7(个),
…,
则第n个图形共有顶点(n+2)(n+3)个,
故选B.反思与感悟 图形中归纳推理的特点及思路
(1)从图形的数量规律入手,找到数值变化与数量的关系.
(2)从图形结构变化规律入手,找到图形的结构每发生一次变化后,与上一次比较,数值发生了怎样的变化.跟踪训练2 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第n个图案中有黑色地面砖的块数是________.解析答案5n+1解析 观察图案知,从第一个图案起,每个图案中黑色地面砖的个数组成首项为6,公差为5的等差数列,从而第n个图案中黑色地面砖的块数为6+(n-1)×5=5n+1.类型二 类比推理解答解 对平面凸四边形:类比在三棱锥中,反思与感悟 (1)类比推理的基本原则是根据当前问题的需要,选择适当的类比对象,可以从几何元素的数目、位置关系、度量等方面入手.由平面中相关结论可以类比得到空间中的相关结论.
(2)平面图形与空间图形的类比如下:解析答案(2)如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边.类比上述定理,写出对空间四面体性质的猜想.解答解 如图所示,在四面体P-ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依
次表示面PAB,面PBC,面PCA与底面ABC所成二面角
的大小.
我们猜想射影定理类比推理到三维空间,其表现形式应为S=S1·cos α+S2·cos β+S3·cos γ.达标检测12341.有一串彩旗,?代表蓝色,?代表黄色.两种彩旗排成一行:
???????????????????????????…,
那么在前200个彩旗中黄旗的个数为
A.111 B.89 C.133 D.67答案√5解析 观察彩旗排列规律可知,颜色的交替成周期性变化,周期为9,每9个旗子中有3个黄旗.则200÷9=22余2,则200个旗子中黄旗的个数为22×3+1=67.故选D.解析2.下列平面图形中,与空间的平行六面体作为类比对象较合适的是
A.三角形 B.梯形
C.平行四边形 D.矩形解析 因为平行六面体相对的两个面互相平行,类比平面图形,则相对的两条边互相平行,故选C.解析答案√123453.观察下列各式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,可以得到的一般结论是
A.n+(n+1)+(n+2)+…+(3n-2)=n2
B.n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2
C.n+(n+1)+(n+2)+…+(3n-1)=n2
D.n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2答案√123454.在平面上,若两个正三角形的边长的比为1∶2,则它们的面积比为1∶4,类似地,在空间上,若两个正四面体的棱长的比为1∶2,则它们的体积比为________.123451∶8解析 设两个正四面体的体积分别为V1,V2,解析答案5.在长方形ABCD中,对角线AC与两邻边所成的角分别为α,β,cos2α+cos2β=1,则在立体几何中,给出类比猜想并证明.12345解答12345解 在长方形ABCD中,于是类比到长方体中,猜想其体对角线与共顶点的三条棱所成的角分别为α,β,γ,则cos2α+cos2β+cos2γ=1.12345证明如下:1.用归纳推理可从具体事例中发现一般规律,但应注意,仅根据一系列有限的特殊事例,所得出的一般结论不一定可靠,其结论的正确与否,还要经过严格的理论证明.
2.进行类比推理时,要尽量从本质上思考,不要被表面现象所迷惑,否则,只抓住一点表面的相似甚至假象就去类比,就会犯机械类比的错误.
3.多用下列技巧会提高所得结论的准确性
(1)类比对象的共同属性或相似属性尽可能的多些.
(2)这些共同属性或相似属性应是类比对象的主要属性.
(3)这些共同(相似)属性应包括类比对象的各个方面,并尽可能是多方面.本课结束
1.了解合情推理的含义,能利用归纳和类比等进行简单的推理.
2.了解合情推理在数学发现中的作用.问题导学达标检测题型探究内容索引问题导学知识点一 推理1.推理的概念与分类
(1)根据一个或几个 得出一个判断,这种思维方式就是推理.
(2)推理一般由两部分组成,一部分是已知的事实(或假设),叫做 ;一部分是由已知推出的判断,叫做 .
(3)推理一般分为 与 .
2.合情推理
前提为真时,结论 的推理,叫做合情推理.常用的合情推理有
和 .已知事实(或假设)前提结论合情推理演绎推理可能为真归纳推理类比推理知识点二 归纳推理思考 (1)铜、铁、铝、金、银等金属都能导电,猜想:一切金属都能导电.
(2)统计学中,从总体中抽取样本,然后用样本估计总体.
以上属于什么推理?答案 属于归纳推理.符合归纳推理的定义特征.梳理 归纳推理
(1)定义:根据一类事物的部分对象具有某种性质,推出这类事物的____
都具有这种性质的推理,叫做归纳推理(简称归纳),归纳是从___
到 的过程.
(2)归纳推理的一般步骤
①通过观察个别情况发现某些 .
②从已知的 中推出一个明确表述的 命题(猜想).所有对象特殊一般相同性质相同性质一般性知识点三 类比推理答案 类比推理.梳理 类比推理
(1)定义:根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另一类事物 的性质的推理,叫做类比推理(简称类比).
(2)类比推理的一般步骤
①找出两类事物之间的 或 .
②用一类事物的性质去推测另一类事物的性质,得出一个 的命题(猜想).类似(或相同)相似性一致性明确1.类比推理得到的结论可作为定理应用.( )
2.由个别到一般的推理为归纳推理.( )
3.在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.( )[思考辨析 判断正误]×√×题型探究命题角度1 数、式中的归纳推理
例1 (1)观察下列等式:
据此规律,第n(n∈N+)个等式可为________________________________
________________.类型一 归纳推理解析答案(2)已知f(x)= ,设f1(x)=f(x),fn(x)=fn-1(fn-1(x))(n>1,且n∈N+),
则f3(x)的表达式为_______________,猜想fn(x)(n∈N+)的表达式为________________.解析答案又∵fn(x)=fn-1(fn-1(x)),引申探究
在本例(2)中,若把“fn(x)=fn-1(fn-1(x))”改为“fn(x)=f(fn-1(x))”,其他条件不变,试猜想fn(x) (n∈N+)的表达式.解答又∵fn(x)=f(fn-1(x)),反思与感悟 (1)已知等式或不等式进行归纳推理的方法
①要特别注意所给几个等式(或不等式)中项数和次数等方面的变化规律;②要特别注意所给几个等式(或不等式)中结构形成的特征;③提炼出等式(或不等式)的综合特点;④运用归纳推理得出一般结论.
(2)数列中的归纳推理:在数列问题中,常常用到归纳推理猜测数列的通项公式或前n项和.
①通过已知条件求出数列的前几项或前n项和;②根据数列中的前几项或前n项和与对应序号之间的关系求解;③运用归纳推理写出数列的通项公式或前n项和公式.√答案解析(2)观察下列等式:答案解析命题角度2 几何中的归纳推理
例2 如图,第n个图形是由正n+2边形“扩展”而来(n=1,2,3,…),则第n个图形中顶点的个数为A.(n+1)(n+2) B.(n+2)(n+3)
C.n2 D.n√答案解析解析 由已知图形我们可以得到:
当n=1时,顶点共有12=3×4(个),
当n=2时,顶点共有20=4×5(个),
当n=3时,顶点共有30=5×6(个),
当n=4时,顶点共有42=6×7(个),
…,
则第n个图形共有顶点(n+2)(n+3)个,
故选B.反思与感悟 图形中归纳推理的特点及思路
(1)从图形的数量规律入手,找到数值变化与数量的关系.
(2)从图形结构变化规律入手,找到图形的结构每发生一次变化后,与上一次比较,数值发生了怎样的变化.跟踪训练2 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第n个图案中有黑色地面砖的块数是________.解析答案5n+1解析 观察图案知,从第一个图案起,每个图案中黑色地面砖的个数组成首项为6,公差为5的等差数列,从而第n个图案中黑色地面砖的块数为6+(n-1)×5=5n+1.类型二 类比推理解答解 对平面凸四边形:类比在三棱锥中,反思与感悟 (1)类比推理的基本原则是根据当前问题的需要,选择适当的类比对象,可以从几何元素的数目、位置关系、度量等方面入手.由平面中相关结论可以类比得到空间中的相关结论.
(2)平面图形与空间图形的类比如下:解析答案(2)如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边.类比上述定理,写出对空间四面体性质的猜想.解答解 如图所示,在四面体P-ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依
次表示面PAB,面PBC,面PCA与底面ABC所成二面角
的大小.
我们猜想射影定理类比推理到三维空间,其表现形式应为S=S1·cos α+S2·cos β+S3·cos γ.达标检测12341.有一串彩旗,?代表蓝色,?代表黄色.两种彩旗排成一行:
???????????????????????????…,
那么在前200个彩旗中黄旗的个数为
A.111 B.89 C.133 D.67答案√5解析 观察彩旗排列规律可知,颜色的交替成周期性变化,周期为9,每9个旗子中有3个黄旗.则200÷9=22余2,则200个旗子中黄旗的个数为22×3+1=67.故选D.解析2.下列平面图形中,与空间的平行六面体作为类比对象较合适的是
A.三角形 B.梯形
C.平行四边形 D.矩形解析 因为平行六面体相对的两个面互相平行,类比平面图形,则相对的两条边互相平行,故选C.解析答案√123453.观察下列各式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,可以得到的一般结论是
A.n+(n+1)+(n+2)+…+(3n-2)=n2
B.n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2
C.n+(n+1)+(n+2)+…+(3n-1)=n2
D.n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2答案√123454.在平面上,若两个正三角形的边长的比为1∶2,则它们的面积比为1∶4,类似地,在空间上,若两个正四面体的棱长的比为1∶2,则它们的体积比为________.123451∶8解析 设两个正四面体的体积分别为V1,V2,解析答案5.在长方形ABCD中,对角线AC与两邻边所成的角分别为α,β,cos2α+cos2β=1,则在立体几何中,给出类比猜想并证明.12345解答12345解 在长方形ABCD中,于是类比到长方体中,猜想其体对角线与共顶点的三条棱所成的角分别为α,β,γ,则cos2α+cos2β+cos2γ=1.12345证明如下:1.用归纳推理可从具体事例中发现一般规律,但应注意,仅根据一系列有限的特殊事例,所得出的一般结论不一定可靠,其结论的正确与否,还要经过严格的理论证明.
2.进行类比推理时,要尽量从本质上思考,不要被表面现象所迷惑,否则,只抓住一点表面的相似甚至假象就去类比,就会犯机械类比的错误.
3.多用下列技巧会提高所得结论的准确性
(1)类比对象的共同属性或相似属性尽可能的多些.
(2)这些共同属性或相似属性应是类比对象的主要属性.
(3)这些共同(相似)属性应包括类比对象的各个方面,并尽可能是多方面.本课结束
