人教版八年级数学上册第十五章 分式15.2.3 整式指数幂 课件(共53张PPT)
文档属性
| 名称 | 人教版八年级数学上册第十五章 分式15.2.3 整式指数幂 课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-04 00:00:00 | ||
图片预览




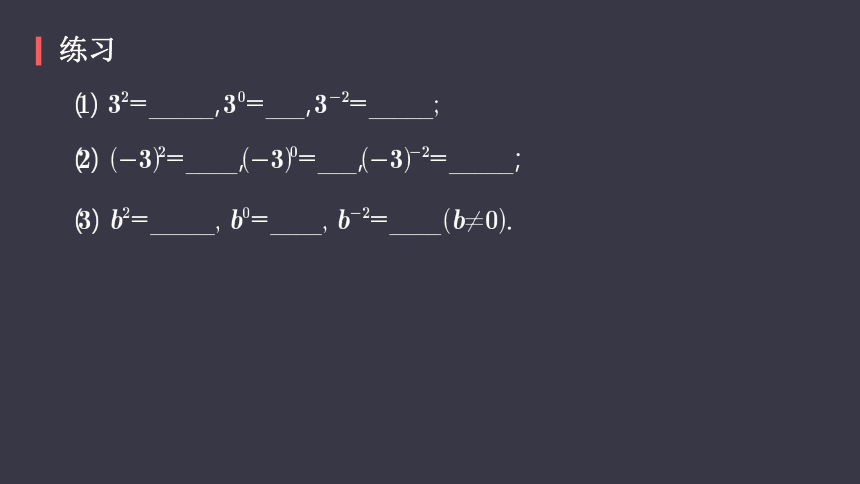
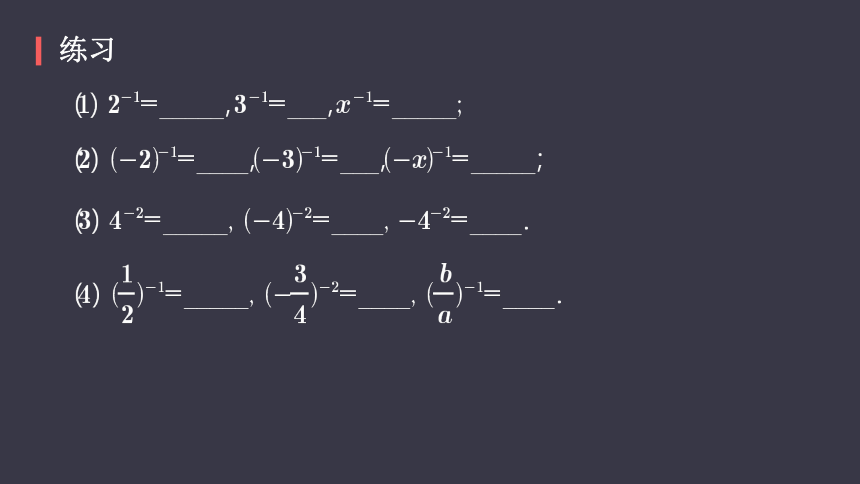





文档简介
(共53张PPT)
整数指数幂
知识回顾
正整数指数幂有哪些运算性质
探究
又
反过来,若规定
=
规定
数学中规定:
当
n
是正整数时,
适用范围更广,同时也更
简便地表示分式,
也就是说,
练习
练习
探究
我们可以从几个特例入手进行探究.
从定义角度
从公式角度
结果一致
再来看几个例子
探究
结果一致
结果一致
结果一致
归纳
这条性质,对于m,n是任意整数的情形仍然适用
类似的,
也能证明
这几条性质,对于m,n是任意整数的情形也适用
整数指数幂的性质
(1)
(3)
(2)
(5)
(4)
(m,n都是整数)
(m,n都是整数)
(m,n都是整数)
(n是整数)
(n是整数)
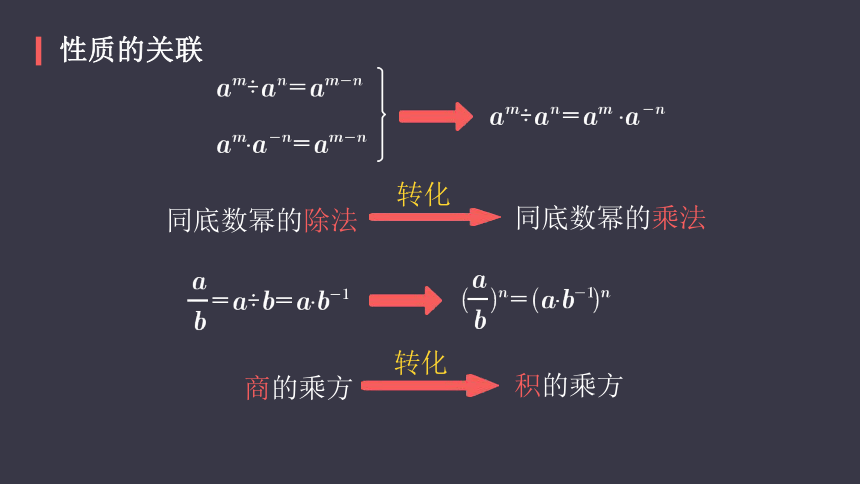
性质的关联
同底数幂的除法
转化
同底数幂的乘法
商的乘方
转化
积的乘方
精简后的性质
(1)
(3)
(2)
(m,n都是整数)
(m,n都是整数)
(n是整数)
例题
计算:
计算:
练习
练习
计算:
练习
补充题
计算:
补充题
思考
一些较大的数适合用科学记数法表示.
你会用科学记数法表示下列这些小于1的数吗?
0.000
01
0.000
025
7
0.000
000
0257
a的整数部分
只能是1~9
光速约为
米/秒
太阳半径约为
千米
2010年世界人口约为
探究
为了解决这个问题,我们先来看几个更简单的问题.
0.001=______=______=______
0.0001=_______=______=______
0.00001=________=______=______
归纳:
有几个0,就是
10的负几次方.
0.00…0.1=
n个0
n个0
探究
0.00001=
0.000
025
7=
0.000
000
0257=
2.57×0.000
01=
2.57×0.000
000
01=
你能发现指数与0的个数的关系吗?
有几个0,指数就是负几
注意:数0的个数时,要从左边开始数,到第一个不为
0的数就结束.
例题
用科学记数法表示下列各数:
(1)0.3;(2)-0.000
78;(3)0.000
020
09.
例题
下列是用科学记数法表示的数,写出原来的数:
练习
用科学记数法表示下列数:
(1)0.000
01;
(2)0.001
2;
(3)0.000
000
345;
(4)0.000
000
010
8.
练习
用科学记数法表示下列各数:
(1)0.003
(2)0.000
098
2
练习
用科学记数法表示下列数:
0.000
000
010
8,
3780
000
0.000
000
345
,
-0.000
03,
0.000
000
001,
0.001
2,
练习
用科学记数法表示:
(1)0.000
03; (2)-0.000
0064;
(3)0.000
0314; (4)2013
000.
补充题
比较大小:
<
<
补充题
用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=________秒;
(2)1毫克=_________千克;
(3)1微米=_________米;
(4)1纳米=_________微米;
(5)1平方厘米=_________平方米;
(6)1毫升=_________立方米.
例题
练习
练习
计算:
总结
这节课我们学会了什么?
2.整数指数幂:
(1)
(3)
(2)
(m,n都是整数)
(m,n都是整数)
(n是整数)
当
n
是正整数时,
也就是说,
1.负整数指数幂:
总结
这节课我们学会了什么?
3.用科学记数法表示小于1的数:
特点:有几个0,指数就是负几
0.00001=
0.000
025
7=
0.000
000
0257=
2.57×0.000
01=
2.57×0.000
000
01=
负整数指数幂有什么性质?
怎么用科学记数法表示小于1的数?
整数指数幂的性质?
整数指数幂
复习巩固
1.
计算:
复习巩固
2.
计算:
复习巩固
3.
计算:
复习巩固
4.
计算:
复习巩固
5.
计算:
复习巩固
6.
计算:
复习巩固
7.
计算:
复习巩固
8.
用科学计数法表示下列数:
0.00001
0.00002
0.000000567
0.000000301.
复习巩固
9.
计算:
综合运用
综合运用
综合运用
12.
绿化队原来用漫灌方式浇绿地,a天用水m
t,现在改用喷灌
方式,可使这些水多用3天,现在比原来每天节约用水多少吨?
综合运用
13.
两地相距n
km,提速前火车从一地到另一地要用t
h,提速
后行车时间减少了0.5
h,
提速后火车的速度比原来速度快了多
少?
综合运用
拓广探索
15.
计算下列两式,探索其中的共同规律:
拓广探索
16.
一个无盖长方体盒子的容积是V.
(1)如果盒子底面是边长为a的正方形,
这个盒子的表面积是多少?
(2)如果盒子底面是长为b、宽为c的长
方形,这个盒子的表面积是多少?
(3)上面两种情况下,如果盒子的底面
面积相等,那么两种盒子的表面积
相差多少?(不计制造材料的厚度.)
容器中的水能倒完吗
请看下面的问题:
①
你可能会想到通过实验探寻问题的答案,但是实验中要精确地测量倒出的水
量,当倒出的水量很小时测量的难度非常大.我们不考虑实际操作因素,将上面
的问题抽象成数学模型加以解决.
容易列出倒n次水倒出的总水量为
容器中的水能倒完吗
根据分式的减法法则,
反过来,有
利用②可以把①改写为
②
③
按这种方法,容器中的1
L水是倒不完的.
整数指数幂
知识回顾
正整数指数幂有哪些运算性质
探究
又
反过来,若规定
=
规定
数学中规定:
当
n
是正整数时,
适用范围更广,同时也更
简便地表示分式,
也就是说,
练习
练习
探究
我们可以从几个特例入手进行探究.
从定义角度
从公式角度
结果一致
再来看几个例子
探究
结果一致
结果一致
结果一致
归纳
这条性质,对于m,n是任意整数的情形仍然适用
类似的,
也能证明
这几条性质,对于m,n是任意整数的情形也适用
整数指数幂的性质
(1)
(3)
(2)
(5)
(4)
(m,n都是整数)
(m,n都是整数)
(m,n都是整数)
(n是整数)
(n是整数)
性质的关联
同底数幂的除法
转化
同底数幂的乘法
商的乘方
转化
积的乘方
精简后的性质
(1)
(3)
(2)
(m,n都是整数)
(m,n都是整数)
(n是整数)
例题
计算:
计算:
练习
练习
计算:
练习
补充题
计算:
补充题
思考
一些较大的数适合用科学记数法表示.
你会用科学记数法表示下列这些小于1的数吗?
0.000
01
0.000
025
7
0.000
000
0257
a的整数部分
只能是1~9
光速约为
米/秒
太阳半径约为
千米
2010年世界人口约为
探究
为了解决这个问题,我们先来看几个更简单的问题.
0.001=______=______=______
0.0001=_______=______=______
0.00001=________=______=______
归纳:
有几个0,就是
10的负几次方.
0.00…0.1=
n个0
n个0
探究
0.00001=
0.000
025
7=
0.000
000
0257=
2.57×0.000
01=
2.57×0.000
000
01=
你能发现指数与0的个数的关系吗?
有几个0,指数就是负几
注意:数0的个数时,要从左边开始数,到第一个不为
0的数就结束.
例题
用科学记数法表示下列各数:
(1)0.3;(2)-0.000
78;(3)0.000
020
09.
例题
下列是用科学记数法表示的数,写出原来的数:
练习
用科学记数法表示下列数:
(1)0.000
01;
(2)0.001
2;
(3)0.000
000
345;
(4)0.000
000
010
8.
练习
用科学记数法表示下列各数:
(1)0.003
(2)0.000
098
2
练习
用科学记数法表示下列数:
0.000
000
010
8,
3780
000
0.000
000
345
,
-0.000
03,
0.000
000
001,
0.001
2,
练习
用科学记数法表示:
(1)0.000
03; (2)-0.000
0064;
(3)0.000
0314; (4)2013
000.
补充题
比较大小:
<
<
补充题
用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=________秒;
(2)1毫克=_________千克;
(3)1微米=_________米;
(4)1纳米=_________微米;
(5)1平方厘米=_________平方米;
(6)1毫升=_________立方米.
例题
练习
练习
计算:
总结
这节课我们学会了什么?
2.整数指数幂:
(1)
(3)
(2)
(m,n都是整数)
(m,n都是整数)
(n是整数)
当
n
是正整数时,
也就是说,
1.负整数指数幂:
总结
这节课我们学会了什么?
3.用科学记数法表示小于1的数:
特点:有几个0,指数就是负几
0.00001=
0.000
025
7=
0.000
000
0257=
2.57×0.000
01=
2.57×0.000
000
01=
负整数指数幂有什么性质?
怎么用科学记数法表示小于1的数?
整数指数幂的性质?
整数指数幂
复习巩固
1.
计算:
复习巩固
2.
计算:
复习巩固
3.
计算:
复习巩固
4.
计算:
复习巩固
5.
计算:
复习巩固
6.
计算:
复习巩固
7.
计算:
复习巩固
8.
用科学计数法表示下列数:
0.00001
0.00002
0.000000567
0.000000301.
复习巩固
9.
计算:
综合运用
综合运用
综合运用
12.
绿化队原来用漫灌方式浇绿地,a天用水m
t,现在改用喷灌
方式,可使这些水多用3天,现在比原来每天节约用水多少吨?
综合运用
13.
两地相距n
km,提速前火车从一地到另一地要用t
h,提速
后行车时间减少了0.5
h,
提速后火车的速度比原来速度快了多
少?
综合运用
拓广探索
15.
计算下列两式,探索其中的共同规律:
拓广探索
16.
一个无盖长方体盒子的容积是V.
(1)如果盒子底面是边长为a的正方形,
这个盒子的表面积是多少?
(2)如果盒子底面是长为b、宽为c的长
方形,这个盒子的表面积是多少?
(3)上面两种情况下,如果盒子的底面
面积相等,那么两种盒子的表面积
相差多少?(不计制造材料的厚度.)
容器中的水能倒完吗
请看下面的问题:
①
你可能会想到通过实验探寻问题的答案,但是实验中要精确地测量倒出的水
量,当倒出的水量很小时测量的难度非常大.我们不考虑实际操作因素,将上面
的问题抽象成数学模型加以解决.
容易列出倒n次水倒出的总水量为
容器中的水能倒完吗
根据分式的减法法则,
反过来,有
利用②可以把①改写为
②
③
按这种方法,容器中的1
L水是倒不完的.
