第1章 1.2.1 排列(2)
文档属性
| 名称 | 第1章 1.2.1 排列(2) |  | |
| 格式 | zip | ||
| 文件大小 | 955.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-07 12:22:23 | ||
图片预览











文档简介
课件55张PPT。第一章——计数原理1.2.1 排列(二)[学习目标]
1.进一步加深对排列概念的理解.
2.掌握几种有限制条件的排列,能应用排列数公式解决简单的实际问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
有限制条件的排列问题的解题思路有哪些?
答 所谓有限制条件的排列问题是指某些元素或位置有特殊要求.解决此类问题常从特殊元素或特殊位置入手进行解决,常用的方法有直接法和间接法,直接法又有分步法和分类法两种.(1)直接法
①分步法
按特殊元素或特殊位置优先安排,再安排一般元素(位置)依次分步解决,特别地:
(ⅰ)当某些特殊元素要求必须相邻时可以先将这些元素看作一个整体,与其他元素排列后,再考虑相邻元素的内部排序,这种分步法称为“捆绑法”,即“相邻元素捆绑法”.(ⅱ)当某些特殊元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入空档,这种方法称为“插空法”,即“不相邻元素插空法”.
②分类法
直接按特殊元素当选情况或特殊位置安排进行分类解决,即直接分类法.特别地当某些元素按一定顺序排列时可用“等机率法”,即n个不同元素参加排列,其中m个元素的顺序是确定的,这类问题的解法采用分类法:n个不同元素的全排列(2)间接法
符合条件数等于无限制条件数与不符合条件数的差.故求符合条件的种数时,可先求与其对应的不符合条件的种数,进而求解,即“间接法”.[预习导引]
1.排列数公式
A =
(n,m∈N+,m≤n) .
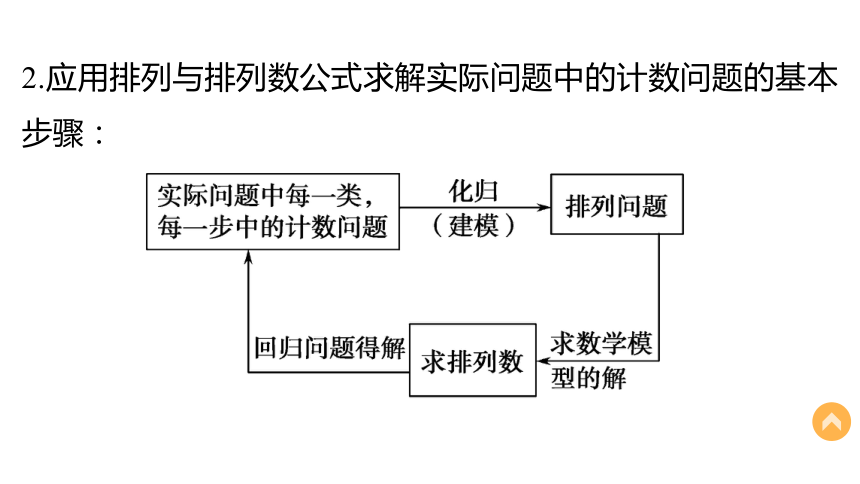
A= = (叫作n的阶乘).另外,我们规定0!= .n(n-1)(n-2)…(n-m+1)n(n-1)(n-2)…2·1n!1= 2.应用排列与排列数公式求解实际问题中的计数问题的基本步骤:要点一 数字排列的问题
例1 用0,1,2,3,4,5这六个数字
(1)可以组成多少个数字不重复的三位数?
解 分三步:
①先选百位数字,由于0不能作百位数字,因此有5种选法;②十位数字有5种选法;③个位数字有4种选法.
由分步乘法计数原理知所求三位数共有5×5×4=100(个).(2)可以组成多少个数字允许重复的三位数?
解 分三步:①百位数字有5种选法;
②十位数字有6种选法;
③个位数字有6种选法.
故所求三位数共有5×6×6=180(个).(3)可以组成多少个数字不允许重复的三位奇数?
解 分三步:①先选个位数字,有3种选法
②再选百位数字,有4种选法;
③选十位数字也有4种选法,
所以所求三位奇数共有3×4×4=48(个).(4)可以组成多少个数字不重复的小于1 000的自然数?
解 分三类:①一位数共有6个;
②两位数共有5×5=25(个);
③三位数共有5×5×4=100(个).
因此,比1 000小的自然数共有6+25+100=131(个).(5)可以组成多少个大于3 000,小于5 421的不重复的四位数?
解 分四类:①千位数字为3,4之一时,共有2×5×4×3=120(个);
②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=48(个);
③千位数字为5,百位数字为4,十位数字为0,1之一时,共有2×3=6(个);④还有5 420也是满足条件的1个.故所求四位数共120+48+6+1=175(个).规律方法 排列问题的本质是“元素”占“位子”问题,有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上,或某个位子上不排某个元素.
解决此类问题的方法主要按“优先”原则,即优先排特殊元素或优先考虑特殊位子,若一个位子安排的元素影响另一个位子的元素个数时,应分类讨论.跟踪演练1 用0,1,2,…,9十个数字可组成多少个满足以下条件的且没有重复数字的数:
(1)五位奇数;
解 要得到五位奇数,末位应从1,3,5,7,9五个数字中取,有5种取法;
取定末位数字后,首位就有除这个数字和0之外的8种不同取法;首末两位取定后,十个数字还有八个数字可供中间的十位、百位与千位三个数位选取,共有A 种不同的排列方法.
因此由分步乘法计数原理共有5×8×A =13 440个没有重复数字的五位奇数.(2)大于30 000的五位偶数.
解 要得偶数,末位应从0,2,4,6,8中选取,而要得比30 000大的五位偶数,可分两类:①末位数字从0,2中选取,则首位可取3,4,5,6,7,8,9中任一个,共有7种选取方法,其余三个数位可从除首末两个数位上的数字之外的八个数字中选取,共A 种取法.所以共有2×7×A 种不同情况.②末位数字从4,6,8中选取,则首位应从3,4,5,6,7,8,9中除去末位数字的六个数字中选取,其余三个数位仍有A 种选法,所以共有3×6×A 种不同情况.由分类加法计数原理,比30 000大的无重复数字的五位偶数共有2×7×A +3×6×A =10 752(个).要点二 排队问题
例2 3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数:
(1)选5名同学排成一行;
解 无限制条件的排列问题,只要从7名同学中任选5名排列,即可得共有N=A =7×6×5×4×3=2 520(种).(2)全体站成一排,其中甲只能在中间或两端;
解 (直接分步法)先考虑甲有A 种方案,再考虑其余6人全排A ,(3)全体站成一排,其中甲、乙必须在两端;
(4)全体站成一排,其中甲不在最左端,乙不在最右端;
解 方法一(直接分类法)
按甲是否在最右端分两类:方法二(间接法)方法三(直接分步法)
按最左端优先安排分步(5)全体站成一排,男、女各站在一起;
解 相邻问题(捆绑法)(6)全体站成一排,男生必须排在一起;
解 (捆绑法)即把所有男生视为一个元素,与4名女生组成5个元素全排,(7)全体站成一排,男生不能排在一起;
解 即不相邻问题(插空法):(8)全体站成一排,男、女生各不相邻;
(9)全体站成一排,甲、乙中间必须有2人;
解 (捆绑法)任取2人与甲、乙组成一个整体,与余下3个元素全排,(10)全体站成一排,甲必须在乙的右边;
解 甲与乙之间的左右关系各占一半,(11)全体站成一排,甲、乙、丙三人自左向右顺序不变;
解 甲、乙、丙自左向右顺序保持不变,(12)排成前后两排,前排3人,后排4人.
规律方法 排队问题的解题策略
排队问题除涉及特殊元素、特殊位置外,还往往涉及相邻、不相邻、定序等问题.
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.(3)对于定序问题,可采用“除阶乘法”解决.即用不限制的排列数除以顺序一定元素的全排列数.跟踪演练2 分别求出符合下列要求的不同排法的种数:
(1)6名学生排3排,前排1人,中排2人,后排3人;(2)6名学生排成一排,甲不在排头也不在排尾;
解 甲不能排头尾,让受特殊限制的甲先选位置,有A
种选法,(3)6人排成一排,甲、乙不相邻.
解 甲、乙不相邻,第一步除甲、乙外的其余4人先排好;
第二步,甲、乙在已排好的4人的左、右及之间的空位中排,要点三 排列的综合应用
例3 从数字0,1,3,5,7中取出不同的三个数作系数,可以组成多少个不同的一元二次方程ax2+bx+c=0?其中有实根的方程有多少个?
解 先考虑组成一元二次方程的问题.由分步乘法计数原理知,共组成一元二次方程方程要有实根,必须满足Δ=b2-4ac≥0.
分类讨论如下:当c≠0时,分析判别式知b只能取5,7中的一个.当b取5时,a,c只能取1,3这两个数,有A 种;由分类加法计数原理知,有实根的一元二次方程共有:规律方法 该例的限制条件较隐蔽,需仔细分析,一元二次方程中a≠0需要考虑到,而对有实根的一元二次方程需有Δ≥0.这里有两层意思:一是a不能为0;二是要保证b2-4ac≥0,所以需先对c能否取0进行分类讨论.实际问题中,既要能观察出是排列问题,又要能搞清哪些是特殊元素,还要根据问题进行合理分类、分步,选择合适的解法.因此需做一定量的排列应用题,逐渐掌握解决问题的基本思想.跟踪演练3 从集合{1,2,3,…,20}中任选出3个不同的数,使这3个数成等差数列,这样的等差数列可以有多少个?解 设a,b,c∈N+,且a,b,c成等差数列,则a+c=2b,
即a+c应是偶数.
因此从1到20这20个数字中任选出三个数成等差数列,
则第一个数与第三个数必同为偶数或同为奇数,而1到20这20个数字中有10个偶数和10个奇数.当第一个和第三个数选定后,中间数被唯一确定.因此,选法只有两类.1.用1,2,3,4,5这5个数字,组成无重复数字的三位数,其中奇数共有( )
A.30个 B.36个
C.40个 D.60个12341234答案 B12342.6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )
A.144 B.120 C.72 D.24
解析 剩余的3个座位共有4个空隙供3人选择就座,D12343.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是________.解析 5张参观券全部分给4人,分给同一人的2张参观券连号,方法数为:1和2,2和3,3和4,4和5,四种连号,其他号码各为一组,分给4人,共有4×A =96种.964.将红、黄、蓝、白、黑5种颜色的小球,放入红、黄、蓝、白、黑5种颜色的小口袋中,若不允许有空袋,且红口袋中不能装入红球,则有________种不同的放法.
解析 ∵红口袋不能装入红球,
∴红球只能放在黄、蓝、白、黑4种颜色的口袋中,12341234答案 96课堂小结
求解排列问题的主要方法:
1.进一步加深对排列概念的理解.
2.掌握几种有限制条件的排列,能应用排列数公式解决简单的实际问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
有限制条件的排列问题的解题思路有哪些?
答 所谓有限制条件的排列问题是指某些元素或位置有特殊要求.解决此类问题常从特殊元素或特殊位置入手进行解决,常用的方法有直接法和间接法,直接法又有分步法和分类法两种.(1)直接法
①分步法
按特殊元素或特殊位置优先安排,再安排一般元素(位置)依次分步解决,特别地:
(ⅰ)当某些特殊元素要求必须相邻时可以先将这些元素看作一个整体,与其他元素排列后,再考虑相邻元素的内部排序,这种分步法称为“捆绑法”,即“相邻元素捆绑法”.(ⅱ)当某些特殊元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入空档,这种方法称为“插空法”,即“不相邻元素插空法”.
②分类法
直接按特殊元素当选情况或特殊位置安排进行分类解决,即直接分类法.特别地当某些元素按一定顺序排列时可用“等机率法”,即n个不同元素参加排列,其中m个元素的顺序是确定的,这类问题的解法采用分类法:n个不同元素的全排列(2)间接法
符合条件数等于无限制条件数与不符合条件数的差.故求符合条件的种数时,可先求与其对应的不符合条件的种数,进而求解,即“间接法”.[预习导引]
1.排列数公式
A =
(n,m∈N+,m≤n) .
A= = (叫作n的阶乘).另外,我们规定0!= .n(n-1)(n-2)…(n-m+1)n(n-1)(n-2)…2·1n!1= 2.应用排列与排列数公式求解实际问题中的计数问题的基本步骤:要点一 数字排列的问题
例1 用0,1,2,3,4,5这六个数字
(1)可以组成多少个数字不重复的三位数?
解 分三步:
①先选百位数字,由于0不能作百位数字,因此有5种选法;②十位数字有5种选法;③个位数字有4种选法.
由分步乘法计数原理知所求三位数共有5×5×4=100(个).(2)可以组成多少个数字允许重复的三位数?
解 分三步:①百位数字有5种选法;
②十位数字有6种选法;
③个位数字有6种选法.
故所求三位数共有5×6×6=180(个).(3)可以组成多少个数字不允许重复的三位奇数?
解 分三步:①先选个位数字,有3种选法
②再选百位数字,有4种选法;
③选十位数字也有4种选法,
所以所求三位奇数共有3×4×4=48(个).(4)可以组成多少个数字不重复的小于1 000的自然数?
解 分三类:①一位数共有6个;
②两位数共有5×5=25(个);
③三位数共有5×5×4=100(个).
因此,比1 000小的自然数共有6+25+100=131(个).(5)可以组成多少个大于3 000,小于5 421的不重复的四位数?
解 分四类:①千位数字为3,4之一时,共有2×5×4×3=120(个);
②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=48(个);
③千位数字为5,百位数字为4,十位数字为0,1之一时,共有2×3=6(个);④还有5 420也是满足条件的1个.故所求四位数共120+48+6+1=175(个).规律方法 排列问题的本质是“元素”占“位子”问题,有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上,或某个位子上不排某个元素.
解决此类问题的方法主要按“优先”原则,即优先排特殊元素或优先考虑特殊位子,若一个位子安排的元素影响另一个位子的元素个数时,应分类讨论.跟踪演练1 用0,1,2,…,9十个数字可组成多少个满足以下条件的且没有重复数字的数:
(1)五位奇数;
解 要得到五位奇数,末位应从1,3,5,7,9五个数字中取,有5种取法;
取定末位数字后,首位就有除这个数字和0之外的8种不同取法;首末两位取定后,十个数字还有八个数字可供中间的十位、百位与千位三个数位选取,共有A 种不同的排列方法.
因此由分步乘法计数原理共有5×8×A =13 440个没有重复数字的五位奇数.(2)大于30 000的五位偶数.
解 要得偶数,末位应从0,2,4,6,8中选取,而要得比30 000大的五位偶数,可分两类:①末位数字从0,2中选取,则首位可取3,4,5,6,7,8,9中任一个,共有7种选取方法,其余三个数位可从除首末两个数位上的数字之外的八个数字中选取,共A 种取法.所以共有2×7×A 种不同情况.②末位数字从4,6,8中选取,则首位应从3,4,5,6,7,8,9中除去末位数字的六个数字中选取,其余三个数位仍有A 种选法,所以共有3×6×A 种不同情况.由分类加法计数原理,比30 000大的无重复数字的五位偶数共有2×7×A +3×6×A =10 752(个).要点二 排队问题
例2 3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数:
(1)选5名同学排成一行;
解 无限制条件的排列问题,只要从7名同学中任选5名排列,即可得共有N=A =7×6×5×4×3=2 520(种).(2)全体站成一排,其中甲只能在中间或两端;
解 (直接分步法)先考虑甲有A 种方案,再考虑其余6人全排A ,(3)全体站成一排,其中甲、乙必须在两端;
(4)全体站成一排,其中甲不在最左端,乙不在最右端;
解 方法一(直接分类法)
按甲是否在最右端分两类:方法二(间接法)方法三(直接分步法)
按最左端优先安排分步(5)全体站成一排,男、女各站在一起;
解 相邻问题(捆绑法)(6)全体站成一排,男生必须排在一起;
解 (捆绑法)即把所有男生视为一个元素,与4名女生组成5个元素全排,(7)全体站成一排,男生不能排在一起;
解 即不相邻问题(插空法):(8)全体站成一排,男、女生各不相邻;
(9)全体站成一排,甲、乙中间必须有2人;
解 (捆绑法)任取2人与甲、乙组成一个整体,与余下3个元素全排,(10)全体站成一排,甲必须在乙的右边;
解 甲与乙之间的左右关系各占一半,(11)全体站成一排,甲、乙、丙三人自左向右顺序不变;
解 甲、乙、丙自左向右顺序保持不变,(12)排成前后两排,前排3人,后排4人.
规律方法 排队问题的解题策略
排队问题除涉及特殊元素、特殊位置外,还往往涉及相邻、不相邻、定序等问题.
(1)对于相邻问题,可采用“捆绑法”解决.即将相邻的元素视为一个整体进行排列.
(2)对于不相邻问题,可采用“插空法”解决.即先排其余的元素,再将不相邻的元素插入空中.(3)对于定序问题,可采用“除阶乘法”解决.即用不限制的排列数除以顺序一定元素的全排列数.跟踪演练2 分别求出符合下列要求的不同排法的种数:
(1)6名学生排3排,前排1人,中排2人,后排3人;(2)6名学生排成一排,甲不在排头也不在排尾;
解 甲不能排头尾,让受特殊限制的甲先选位置,有A
种选法,(3)6人排成一排,甲、乙不相邻.
解 甲、乙不相邻,第一步除甲、乙外的其余4人先排好;
第二步,甲、乙在已排好的4人的左、右及之间的空位中排,要点三 排列的综合应用
例3 从数字0,1,3,5,7中取出不同的三个数作系数,可以组成多少个不同的一元二次方程ax2+bx+c=0?其中有实根的方程有多少个?
解 先考虑组成一元二次方程的问题.由分步乘法计数原理知,共组成一元二次方程方程要有实根,必须满足Δ=b2-4ac≥0.
分类讨论如下:当c≠0时,分析判别式知b只能取5,7中的一个.当b取5时,a,c只能取1,3这两个数,有A 种;由分类加法计数原理知,有实根的一元二次方程共有:规律方法 该例的限制条件较隐蔽,需仔细分析,一元二次方程中a≠0需要考虑到,而对有实根的一元二次方程需有Δ≥0.这里有两层意思:一是a不能为0;二是要保证b2-4ac≥0,所以需先对c能否取0进行分类讨论.实际问题中,既要能观察出是排列问题,又要能搞清哪些是特殊元素,还要根据问题进行合理分类、分步,选择合适的解法.因此需做一定量的排列应用题,逐渐掌握解决问题的基本思想.跟踪演练3 从集合{1,2,3,…,20}中任选出3个不同的数,使这3个数成等差数列,这样的等差数列可以有多少个?解 设a,b,c∈N+,且a,b,c成等差数列,则a+c=2b,
即a+c应是偶数.
因此从1到20这20个数字中任选出三个数成等差数列,
则第一个数与第三个数必同为偶数或同为奇数,而1到20这20个数字中有10个偶数和10个奇数.当第一个和第三个数选定后,中间数被唯一确定.因此,选法只有两类.1.用1,2,3,4,5这5个数字,组成无重复数字的三位数,其中奇数共有( )
A.30个 B.36个
C.40个 D.60个12341234答案 B12342.6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )
A.144 B.120 C.72 D.24
解析 剩余的3个座位共有4个空隙供3人选择就座,D12343.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是________.解析 5张参观券全部分给4人,分给同一人的2张参观券连号,方法数为:1和2,2和3,3和4,4和5,四种连号,其他号码各为一组,分给4人,共有4×A =96种.964.将红、黄、蓝、白、黑5种颜色的小球,放入红、黄、蓝、白、黑5种颜色的小口袋中,若不允许有空袋,且红口袋中不能装入红球,则有________种不同的放法.
解析 ∵红口袋不能装入红球,
∴红球只能放在黄、蓝、白、黑4种颜色的口袋中,12341234答案 96课堂小结
求解排列问题的主要方法:
