第1章 1.3.2 杨辉三角
图片预览










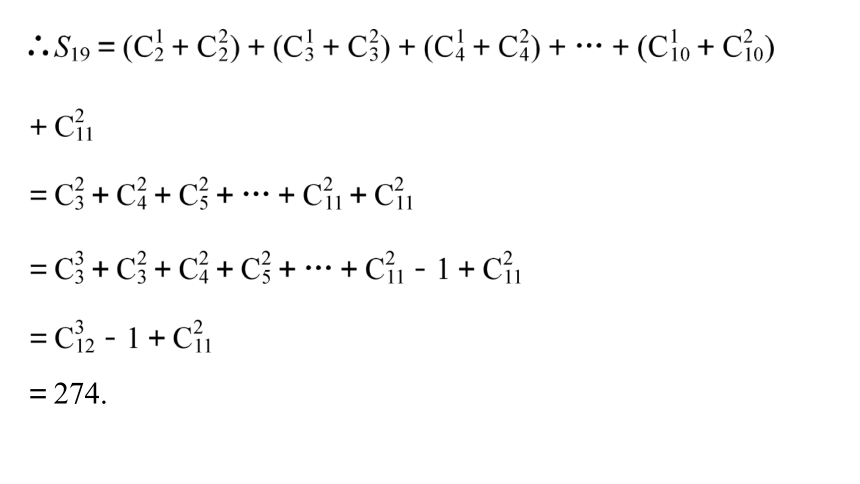

文档简介
课件45张PPT。第一章——计数原理[学习目标]
1.了解杨辉三角,会用杨辉三角求二项式乘方次数不大时的各项的二项式系数.
2.理解二项式系数的性质并灵活运用.1.3 二项式定理
1.3.2 杨辉三角1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.二项式系数表与杨辉三角中对应行的数值都相同吗?
答 不是.二项式系数表中第一行是两个数,而杨辉三角的第一行只有一个数.实际上二项式系数表中的第n行与杨辉三角中的第n+1行对应数值相等.2.根据杨辉三角的第1个规律,同一行中与两个1等距离的项的系数相等,你可以得到二项式系数的什么性质?3.二项式系数何时取得最大值?[预习导引]
二项式系数的性质
(1)每一行的两端都是1,其余每个数都等于它“肩上”两个数的 .
(2)每一行中,与首末两端“等距离”的两个数 .和相等(3)如果二项式的幂指数n是偶数,那么T 项的二项式系数最大;如果n是奇数,那么T 与T 项的二项式系数相等且最大.
(4)二项展开式的二项式系数的和等于 .2n要点一 与杨辉三角有关的问题
例1 如图在“杨辉三角”中,斜线AB的上方,从1开始箭头所示的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,记其前n项和为Sn,求S19的值.…,=274.规律方法 解决与杨辉三角有关的问题的一般思路是:通过观察找出每一行数据间的相互联系以及行与行间数据的相互联系.然后将数据间的这种联系用数学式子表达出来,使问题得解.注意观察方向:横看、竖看、斜看、连续看、隔行看,从多角度观察.跟踪演练1 如图,在由二项式系数所构成的杨辉三角中,第________行中从左到右第14与第15个数的比为2∶3.
第0行1
第1行1 1
第2行1 2 1
第3行1 3 3 1
第4行1 4 6 4 1
第5行1 5 10 10 5 1
… … …解析 设第n行从左至右第14与第15个数之比为2∶3,答案 34要点二 二项展开式的系数和问题
例2 已知(1-2x)7=a0+a1x+a2x2+…+a7x7,求下列各式的值.
(1)a1+a2+…+a7;
解 令x=1,则a0+a1+a2+a3+…+a7=-1.①
令x=-1,则a0-a1+a2-…-a7=37.②
令x=0,得a0=1,代入①中得:
a1+a2+a3+…+a7=-2.(2)a1+a3+a5+a7;
解 由①-②得2a1+2a3+2a5+2a7=-1-37,(3)a0+a2+a4+a6;
解 由①+②得2a0+2a2+2a4+2a6=-1+37,(4)|a0|+|a1|+|a2|+…+|a7|.
解 方法一 ∵(1-2x)7的展开式中,a0,a2,a4,a6大于零,而a1,a3,a5,a7小于零,
∴|a0|+|a1|+|a2|+…+|a7|
=(a0+a2+a4+a6)-(a1+a3+a5+a7)
=1 093-(-1 094)=2 187.方法二 |a0|+|a1|+|a2|+…+|a7|是(1+2x)7展开式中各项的系数和,
令x=1,
∴|a0|+|a1|+…+|a7|=37=2 187.规律方法 赋值法是求二项展开式系数及有关问题的常用方法,注意取值要有利于问题的解决,可以取一个值或几个值,也可以取几组值,解决问题时要避免漏项.一般地,对于多项式f(x)=a0+a1x+a2x2+…+anxn,各项系数和为f(1),奇次项系数和为 [f(1)-f(-1)],偶次项系数和为 [f(1)+f(-1)],a0=f(0).跟踪演练2 设(2- x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
(1)a0;或令x=0,则展开式可化为a0=2100.(2)a1+a2+…+a100;(3)a1+a3+a5+…+a99;
解 令x=-1,与①联立相减可得(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.
解 原式=[(a0+a2+…+a100)+(a1+a3+…+a99)]·[(a0+a2+…+a100)-(a1+a3+…+a99)]
=(a0+a1+a2+…+a100)(a0-a1+a2-a3+…+a98-a99+a100)要点三 求二项展开式中的最大项问题
例3 已知f(x)=( +3x2)n展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
解 令x=1,则二项式各项系数的和为f(1)=(1+3)n=4n,又展开式中各项的二项式系数之和为2n.
由题意知,4n-2n=992.∴(2n)2-2n-992=0,
∴(2n+31)(2n-32)=0,
∴2n=-31(舍),或2n=32,
∴n=5.
由于n=5为奇数,所以展开式中二项式系数最大的项为中间两项,它们分别是(2)求展开式中系数最大的项.∵r∈N,
∴r=4.规律方法 (1)求二项式系数最大的项,要依据二项式系数的性质对(a+b)n中的n进行讨论,n为奇数时中间两项的二项式系数最大;n为偶数时,中间一项的二项式系数最大.(2)求展开式中系数最大项与求二项式系数最大项是不同的.求展开式系数最大的项,如求(a+bx)n(a、b∈R)展开式中系数最大的项,一般是采用待定系数法.设展开式各项系数分别为
A1,A2,…An+1,且第r+1项系数最大,应用
解出r来,即得系数最大的项.跟踪演练3 在(3x-2y)20的展开式中,求
(1)二项式系数最大的项;
解 二项式系数最大的项是第11项,(2)系数绝对值最大的项;
解 设系数绝对值最大的项是r+1项,于是所以r=8,(3)系数最大的项.
解 由于系数为正的项为y的偶次方项,
由(2)知,T9为系数绝对值最大的项,
又T9中y的次数为8,所以T9为所有y的偶次方项中系数最大项,
即展开式的系数最大项,
且T9=C ·312·28·x12y8.1.(1+x)2n+1的展开式中,二项式系数最大的项的项数是( )
A.n,n+1 B.n-1,n
C.n+1,n+2 D.n+2,n+31234解析 (1+x)2n+1展开式有2n+2项.系数最大的项是中间两项,是第n+1项与第n+2项,它们的二项式系数为 C1232.(x- )10的展开式中,系数最大的项是( )
A.第6项 B.第3项
C.第3项和第6项 D.第5项和第7项D41233.在(x+y)n的展开式中,第4项与第8项的系数相等,则展开式中系数最大的项是( )
A.第6项 B.第5项
C.第5,6项 D.第6,7项4123解析 由题意,得第4项与第8项的系数相等,则其二项式系数也相等,4∴展开式中二项式系数最大的项为第6项,它也是系数最大的项.答案 A1234.设(x2+1)(2x+1)9=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a0+a1+a2+…+a11的值为( )
A.-2 B.-1
C.1 D.24123解析 令x=-1,
则原式化为[(-1)2+1][2×(-1)+1]9=a0+a1(2-1)+a2(2-1)2+…+a11(2-1)11,
∴a0+a1+a2+…+a11=-2.
答案 A4课堂小结
1.二项式系数的性质可从杨辉三角中直观地看出.
2.求展开式中的系数或展开式中的系数的和、差的关键是给字母赋值,赋值的选择则需根据所求的展开式系数和特征来确定.一般地对字母赋的值为0,1或-1,但在解决具体问题时要灵活掌握.3.注意以下两点:(1)区分开二项式系数与项的系数.
(2)求解有关系数最大时的不等式组时,注意其中r∈{0,1,2,…,n}的范围.
1.了解杨辉三角,会用杨辉三角求二项式乘方次数不大时的各项的二项式系数.
2.理解二项式系数的性质并灵活运用.1.3 二项式定理
1.3.2 杨辉三角1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.二项式系数表与杨辉三角中对应行的数值都相同吗?
答 不是.二项式系数表中第一行是两个数,而杨辉三角的第一行只有一个数.实际上二项式系数表中的第n行与杨辉三角中的第n+1行对应数值相等.2.根据杨辉三角的第1个规律,同一行中与两个1等距离的项的系数相等,你可以得到二项式系数的什么性质?3.二项式系数何时取得最大值?[预习导引]
二项式系数的性质
(1)每一行的两端都是1,其余每个数都等于它“肩上”两个数的 .
(2)每一行中,与首末两端“等距离”的两个数 .和相等(3)如果二项式的幂指数n是偶数,那么T 项的二项式系数最大;如果n是奇数,那么T 与T 项的二项式系数相等且最大.
(4)二项展开式的二项式系数的和等于 .2n要点一 与杨辉三角有关的问题
例1 如图在“杨辉三角”中,斜线AB的上方,从1开始箭头所示的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,记其前n项和为Sn,求S19的值.…,=274.规律方法 解决与杨辉三角有关的问题的一般思路是:通过观察找出每一行数据间的相互联系以及行与行间数据的相互联系.然后将数据间的这种联系用数学式子表达出来,使问题得解.注意观察方向:横看、竖看、斜看、连续看、隔行看,从多角度观察.跟踪演练1 如图,在由二项式系数所构成的杨辉三角中,第________行中从左到右第14与第15个数的比为2∶3.
第0行1
第1行1 1
第2行1 2 1
第3行1 3 3 1
第4行1 4 6 4 1
第5行1 5 10 10 5 1
… … …解析 设第n行从左至右第14与第15个数之比为2∶3,答案 34要点二 二项展开式的系数和问题
例2 已知(1-2x)7=a0+a1x+a2x2+…+a7x7,求下列各式的值.
(1)a1+a2+…+a7;
解 令x=1,则a0+a1+a2+a3+…+a7=-1.①
令x=-1,则a0-a1+a2-…-a7=37.②
令x=0,得a0=1,代入①中得:
a1+a2+a3+…+a7=-2.(2)a1+a3+a5+a7;
解 由①-②得2a1+2a3+2a5+2a7=-1-37,(3)a0+a2+a4+a6;
解 由①+②得2a0+2a2+2a4+2a6=-1+37,(4)|a0|+|a1|+|a2|+…+|a7|.
解 方法一 ∵(1-2x)7的展开式中,a0,a2,a4,a6大于零,而a1,a3,a5,a7小于零,
∴|a0|+|a1|+|a2|+…+|a7|
=(a0+a2+a4+a6)-(a1+a3+a5+a7)
=1 093-(-1 094)=2 187.方法二 |a0|+|a1|+|a2|+…+|a7|是(1+2x)7展开式中各项的系数和,
令x=1,
∴|a0|+|a1|+…+|a7|=37=2 187.规律方法 赋值法是求二项展开式系数及有关问题的常用方法,注意取值要有利于问题的解决,可以取一个值或几个值,也可以取几组值,解决问题时要避免漏项.一般地,对于多项式f(x)=a0+a1x+a2x2+…+anxn,各项系数和为f(1),奇次项系数和为 [f(1)-f(-1)],偶次项系数和为 [f(1)+f(-1)],a0=f(0).跟踪演练2 设(2- x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
(1)a0;或令x=0,则展开式可化为a0=2100.(2)a1+a2+…+a100;(3)a1+a3+a5+…+a99;
解 令x=-1,与①联立相减可得(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.
解 原式=[(a0+a2+…+a100)+(a1+a3+…+a99)]·[(a0+a2+…+a100)-(a1+a3+…+a99)]
=(a0+a1+a2+…+a100)(a0-a1+a2-a3+…+a98-a99+a100)要点三 求二项展开式中的最大项问题
例3 已知f(x)=( +3x2)n展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
解 令x=1,则二项式各项系数的和为f(1)=(1+3)n=4n,又展开式中各项的二项式系数之和为2n.
由题意知,4n-2n=992.∴(2n)2-2n-992=0,
∴(2n+31)(2n-32)=0,
∴2n=-31(舍),或2n=32,
∴n=5.
由于n=5为奇数,所以展开式中二项式系数最大的项为中间两项,它们分别是(2)求展开式中系数最大的项.∵r∈N,
∴r=4.规律方法 (1)求二项式系数最大的项,要依据二项式系数的性质对(a+b)n中的n进行讨论,n为奇数时中间两项的二项式系数最大;n为偶数时,中间一项的二项式系数最大.(2)求展开式中系数最大项与求二项式系数最大项是不同的.求展开式系数最大的项,如求(a+bx)n(a、b∈R)展开式中系数最大的项,一般是采用待定系数法.设展开式各项系数分别为
A1,A2,…An+1,且第r+1项系数最大,应用
解出r来,即得系数最大的项.跟踪演练3 在(3x-2y)20的展开式中,求
(1)二项式系数最大的项;
解 二项式系数最大的项是第11项,(2)系数绝对值最大的项;
解 设系数绝对值最大的项是r+1项,于是所以r=8,(3)系数最大的项.
解 由于系数为正的项为y的偶次方项,
由(2)知,T9为系数绝对值最大的项,
又T9中y的次数为8,所以T9为所有y的偶次方项中系数最大项,
即展开式的系数最大项,
且T9=C ·312·28·x12y8.1.(1+x)2n+1的展开式中,二项式系数最大的项的项数是( )
A.n,n+1 B.n-1,n
C.n+1,n+2 D.n+2,n+31234解析 (1+x)2n+1展开式有2n+2项.系数最大的项是中间两项,是第n+1项与第n+2项,它们的二项式系数为 C1232.(x- )10的展开式中,系数最大的项是( )
A.第6项 B.第3项
C.第3项和第6项 D.第5项和第7项D41233.在(x+y)n的展开式中,第4项与第8项的系数相等,则展开式中系数最大的项是( )
A.第6项 B.第5项
C.第5,6项 D.第6,7项4123解析 由题意,得第4项与第8项的系数相等,则其二项式系数也相等,4∴展开式中二项式系数最大的项为第6项,它也是系数最大的项.答案 A1234.设(x2+1)(2x+1)9=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a0+a1+a2+…+a11的值为( )
A.-2 B.-1
C.1 D.24123解析 令x=-1,
则原式化为[(-1)2+1][2×(-1)+1]9=a0+a1(2-1)+a2(2-1)2+…+a11(2-1)11,
∴a0+a1+a2+…+a11=-2.
答案 A4课堂小结
1.二项式系数的性质可从杨辉三角中直观地看出.
2.求展开式中的系数或展开式中的系数的和、差的关键是给字母赋值,赋值的选择则需根据所求的展开式系数和特征来确定.一般地对字母赋的值为0,1或-1,但在解决具体问题时要灵活掌握.3.注意以下两点:(1)区分开二项式系数与项的系数.
(2)求解有关系数最大时的不等式组时,注意其中r∈{0,1,2,…,n}的范围.
