第2章 2.3.2 离散型随机变量的方差
文档属性
| 名称 | 第2章 2.3.2 离散型随机变量的方差 |

|
|
| 格式 | zip | ||
| 文件大小 | 805.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-07 00:00:00 | ||
图片预览










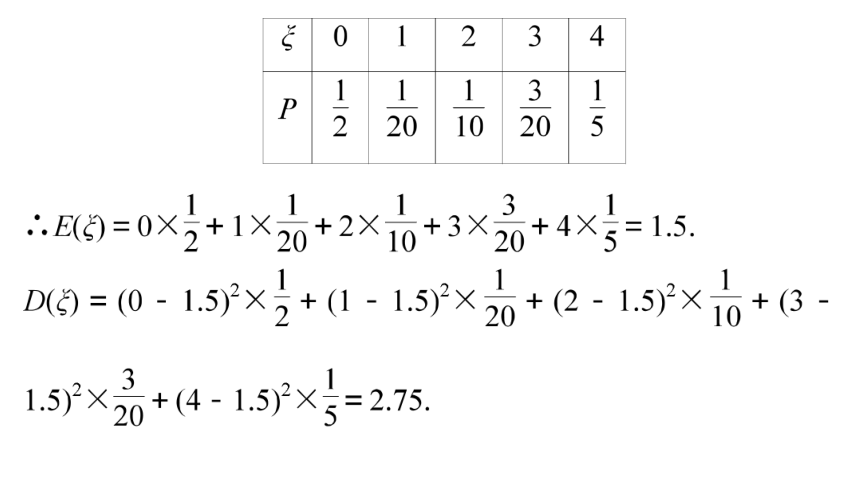

文档简介
课件45张PPT。第二章——概 率2.3.2 离散型随机变量的方差[学习目标]
1.理解取有限个值的离散型随机变量的方差及标准差的概念.
2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
3.掌握方差的性质,以及两点分布、二项分布的方差的求法,会利用公式求它们的方差.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.某省运会即将举行,在最后一次射击选拔比赛中,甲、乙两名运动员各射击10次,命中环数如下:
甲运动员:7,8,6,8,6,5,8,10,7,5;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述数据,两个人射击的平均成绩是一样的.那么,是否两个人就没有水平差距呢?如果你是教练,选哪位选手去参加正式比赛?∴乙成绩较稳定,选乙参加比赛.2.随机变量的方差与样本的方差有何不同?
答 样本的方差是随着样本的不同而变化的,因此它是一个随机变量,而随机变量的方差是通过大量试验得出的,刻画了随机变量X与其均值E(X)的平均偏离程度,因此它是一个常量而非变量.[预习导引]
1.离散型随机变量的方差、标准差
一般地,设一个离散型随机变量X所有可能取的值是x1,x2,…, xn,这些值对应的概率是p1,p2,…,pn,则D(X)=____________
叫做这个离散型随机变量X的方差.离散型随机变量的方差反映了离散型随机变量取值相对于期望的 (或说离散程度).D(X)的算术平方根
叫做离散型随机变量X的 .(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-E(X))2·pn平均波动大小标准差2.离散型随机变量方差的性质
(1)设a,b为常数,则D(aX+b)= ;
(2)D(c)=0(其中c为常数).a2D(X)3.服从两点分布与二项分布的随机变量的方差
(1)若X服从两点分布,则D(X)= (其中p为成功概率);
(2)若X~B(n,p),则D(X)= .p(1-p)np(1-p)要点一 求离散型随机变量的方差
例1 袋中有20个大小相同的球,其中标有0号的有10个,标有n号的有n个(n=1,2,3,4).现从袋中任取一球,ξ表示所取球的标号.
(1)求ξ的分布列、期望和方差;
解 ξ的分布列为(2)若η=aξ+b,E(η)=1,D(η)=11,试求a,b的值.
解 由D(η)=a2D(ξ),得a2×2.75=11,即a=±2.
又E(η)=aE(ξ)+b,
所以当a=2时,由1=2×1.5+b,得b=-2.
当a=-2时,由1=-2×1.5+b,得b=4.规律方法 1.求离散型随机变量的方差的类型及解决方法
(1)已知分布列(非两点分布或二项分布):直接利用定义求解,先求均值,再求方差.
(2)已知分布列是两点分布或二项分布型:直接套用公式求解,具体如下:
①若X服从两点分布,则D(X)=p(1-p).
②若X~B(n,p),则D(X)=np(1-p).(3)分布列未知:求解时可先借助已知条件及概率知识先求得分布列,然后转化成(1)中的情况.
(4)对于已知D(X)求D(aX+b)型,利用方差的性质求解,即利用D(aX+b)=a2D(X)求解.2.求离散型随机变量ξ的方差、标准差的步骤
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ), .若ξ~B(n,p),则不必写出分布列,直接用公式计算即可.跟踪演练1 甲、乙两人进行定点投篮游戏,投篮者若投中,则继续投篮,否则由对方投篮,第一次由甲投篮;已知每次投篮甲、乙命中的概率分别为
(1)求第三次由乙投篮的概率;(2)在前3次投篮中,乙投篮的次数为ξ,求ξ的分布列、期望及标准差.故ξ的分布列为要点二 两点分布与二项分布的方差
例2 为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设ξ为成活沙柳的株数,数学期望E(ξ)为3,标准差为(1)求n和p的值,并写出ξ的分布列;
解 由题意知,ξ服从二项分布B(n,p),ξ的分布列为(2)若有3株或3株以上的沙柳未成活,则需要补种.求需要补种沙柳的概率.
解 记“需要补种沙柳”为事件A,则P(A)=P(ξ≤3),规律方法 方差的性质:D(aξ+b)=a2D(ξ).若ξ服从两点分布,则D(ξ)=p(1-p).若ξ~B(n,p),则D(ξ)=np(1-p).跟踪演练2 设一次试验的成功率为p,进行100次独立重复试验,求当p为何值时,成功次数的标准差的值最大?并求其最大值.
解 设成功次数为随机变量X,因为D(X)=100p(1-p)=100p-100p2,把上式看作一个以p为自变量的二次函数,要点三 期望与方差的综合应用
例3 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
解 当日需求量n≥16时,利润y=80.当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差.解 X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为X的数学期望为E(X)=60×0.1+70×0.2+80×0.7=76.
X的方差为D(X)=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.规律方法 解期望与方差的综合问题时的注意事项
(1)离散型随机变量的分布列、期望和方差是三个紧密联系的有机统一体,一般在试题中综合在一起考查,其解题的关键是求出分布列;
(2)在求分布列时,要注意利用等可能事件、互斥事件、相互独立事件的概率公式计算概率,并注意结合分布列的性质,简化概率计算;(3)在计算期望与方差时要注意运用期望和方差的性质以避免一些复杂的计算.若随机变量X服从两点分布、二项分布可直接利用对应公式求解.跟踪演练3 从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生的人数.
(1)求X的分布列;X的分布列(2)求X的均值与方差;
解 由(1),X的均值与方差为(3)求“所选3人中女生人数X≤1”的概率.
解 由(1),“所选3人中女生人数X≤1”的概率为1.设随机变量X的方差D(X)=1,则D(2X+1)的值为( )
A.2 B.3 C.4 D.5
解析 D(2X+1)=4D(X)=4×1=4.1234C12342.同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)等于( )A12343.已知离散型随机变量X的可能取值为x1=-1,x2=0,x3=1,且E(X)=0.1,D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,________,________.
解析 由题意知,-p1+p3=0.1,
1.21p1+0.01p2+0.81p3=0.89.
又p1+p2+p3=1,解得p1=0.4,p2=0.1,p3=0.5.0.40.10.54.同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为ξ.
(1)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
解 设“抛掷4枚硬币,恰好2枚正面向上,2枚反面向上”为事件A,抛掷4枚硬币的基本事件总数是24,123412341234(2)求ξ的数学期望和方差.
1234课堂小结1.随机变量的方差和标准差都反映了随机变量取值的稳定与波动、集中与离散的程度,以及随机变量取值偏离于期望的平均程度.方差D(X)或标准差越小,则随机变量X偏离期望的平均程度越小;方差越大,表明平均偏离的程度越大,说明X的取值越分散.2.求离散型随机变量X的期望、方差的步骤
(1)理解X的意义,写出X的所有可能的取值;
(2)求X取每一个值的概率;
(3)写出随机变量X的分布列;
(4)由期望、方差的定义求E(X),D(X).
特别地,若随机变量服从两点分布或二项分布,可根据公式直接计算E(X)和D(X).
1.理解取有限个值的离散型随机变量的方差及标准差的概念.
2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
3.掌握方差的性质,以及两点分布、二项分布的方差的求法,会利用公式求它们的方差.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.某省运会即将举行,在最后一次射击选拔比赛中,甲、乙两名运动员各射击10次,命中环数如下:
甲运动员:7,8,6,8,6,5,8,10,7,5;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述数据,两个人射击的平均成绩是一样的.那么,是否两个人就没有水平差距呢?如果你是教练,选哪位选手去参加正式比赛?∴乙成绩较稳定,选乙参加比赛.2.随机变量的方差与样本的方差有何不同?
答 样本的方差是随着样本的不同而变化的,因此它是一个随机变量,而随机变量的方差是通过大量试验得出的,刻画了随机变量X与其均值E(X)的平均偏离程度,因此它是一个常量而非变量.[预习导引]
1.离散型随机变量的方差、标准差
一般地,设一个离散型随机变量X所有可能取的值是x1,x2,…, xn,这些值对应的概率是p1,p2,…,pn,则D(X)=____________
叫做这个离散型随机变量X的方差.离散型随机变量的方差反映了离散型随机变量取值相对于期望的 (或说离散程度).D(X)的算术平方根
叫做离散型随机变量X的 .(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-E(X))2·pn平均波动大小标准差2.离散型随机变量方差的性质
(1)设a,b为常数,则D(aX+b)= ;
(2)D(c)=0(其中c为常数).a2D(X)3.服从两点分布与二项分布的随机变量的方差
(1)若X服从两点分布,则D(X)= (其中p为成功概率);
(2)若X~B(n,p),则D(X)= .p(1-p)np(1-p)要点一 求离散型随机变量的方差
例1 袋中有20个大小相同的球,其中标有0号的有10个,标有n号的有n个(n=1,2,3,4).现从袋中任取一球,ξ表示所取球的标号.
(1)求ξ的分布列、期望和方差;
解 ξ的分布列为(2)若η=aξ+b,E(η)=1,D(η)=11,试求a,b的值.
解 由D(η)=a2D(ξ),得a2×2.75=11,即a=±2.
又E(η)=aE(ξ)+b,
所以当a=2时,由1=2×1.5+b,得b=-2.
当a=-2时,由1=-2×1.5+b,得b=4.规律方法 1.求离散型随机变量的方差的类型及解决方法
(1)已知分布列(非两点分布或二项分布):直接利用定义求解,先求均值,再求方差.
(2)已知分布列是两点分布或二项分布型:直接套用公式求解,具体如下:
①若X服从两点分布,则D(X)=p(1-p).
②若X~B(n,p),则D(X)=np(1-p).(3)分布列未知:求解时可先借助已知条件及概率知识先求得分布列,然后转化成(1)中的情况.
(4)对于已知D(X)求D(aX+b)型,利用方差的性质求解,即利用D(aX+b)=a2D(X)求解.2.求离散型随机变量ξ的方差、标准差的步骤
(1)理解ξ的意义,写出ξ可能取的全部值.
(2)求ξ取各个值的概率,写出分布列.
(3)根据分布列,由期望的定义求出E(ξ).
(4)根据方差、标准差的定义求出D(ξ), .若ξ~B(n,p),则不必写出分布列,直接用公式计算即可.跟踪演练1 甲、乙两人进行定点投篮游戏,投篮者若投中,则继续投篮,否则由对方投篮,第一次由甲投篮;已知每次投篮甲、乙命中的概率分别为
(1)求第三次由乙投篮的概率;(2)在前3次投篮中,乙投篮的次数为ξ,求ξ的分布列、期望及标准差.故ξ的分布列为要点二 两点分布与二项分布的方差
例2 为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设ξ为成活沙柳的株数,数学期望E(ξ)为3,标准差为(1)求n和p的值,并写出ξ的分布列;
解 由题意知,ξ服从二项分布B(n,p),ξ的分布列为(2)若有3株或3株以上的沙柳未成活,则需要补种.求需要补种沙柳的概率.
解 记“需要补种沙柳”为事件A,则P(A)=P(ξ≤3),规律方法 方差的性质:D(aξ+b)=a2D(ξ).若ξ服从两点分布,则D(ξ)=p(1-p).若ξ~B(n,p),则D(ξ)=np(1-p).跟踪演练2 设一次试验的成功率为p,进行100次独立重复试验,求当p为何值时,成功次数的标准差的值最大?并求其最大值.
解 设成功次数为随机变量X,因为D(X)=100p(1-p)=100p-100p2,把上式看作一个以p为自变量的二次函数,要点三 期望与方差的综合应用
例3 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
解 当日需求量n≥16时,利润y=80.当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差.解 X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为X的数学期望为E(X)=60×0.1+70×0.2+80×0.7=76.
X的方差为D(X)=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.规律方法 解期望与方差的综合问题时的注意事项
(1)离散型随机变量的分布列、期望和方差是三个紧密联系的有机统一体,一般在试题中综合在一起考查,其解题的关键是求出分布列;
(2)在求分布列时,要注意利用等可能事件、互斥事件、相互独立事件的概率公式计算概率,并注意结合分布列的性质,简化概率计算;(3)在计算期望与方差时要注意运用期望和方差的性质以避免一些复杂的计算.若随机变量X服从两点分布、二项分布可直接利用对应公式求解.跟踪演练3 从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生的人数.
(1)求X的分布列;X的分布列(2)求X的均值与方差;
解 由(1),X的均值与方差为(3)求“所选3人中女生人数X≤1”的概率.
解 由(1),“所选3人中女生人数X≤1”的概率为1.设随机变量X的方差D(X)=1,则D(2X+1)的值为( )
A.2 B.3 C.4 D.5
解析 D(2X+1)=4D(X)=4×1=4.1234C12342.同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)等于( )A12343.已知离散型随机变量X的可能取值为x1=-1,x2=0,x3=1,且E(X)=0.1,D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,________,________.
解析 由题意知,-p1+p3=0.1,
1.21p1+0.01p2+0.81p3=0.89.
又p1+p2+p3=1,解得p1=0.4,p2=0.1,p3=0.5.0.40.10.54.同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为ξ.
(1)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
解 设“抛掷4枚硬币,恰好2枚正面向上,2枚反面向上”为事件A,抛掷4枚硬币的基本事件总数是24,123412341234(2)求ξ的数学期望和方差.
1234课堂小结1.随机变量的方差和标准差都反映了随机变量取值的稳定与波动、集中与离散的程度,以及随机变量取值偏离于期望的平均程度.方差D(X)或标准差越小,则随机变量X偏离期望的平均程度越小;方差越大,表明平均偏离的程度越大,说明X的取值越分散.2.求离散型随机变量X的期望、方差的步骤
(1)理解X的意义,写出X的所有可能的取值;
(2)求X取每一个值的概率;
(3)写出随机变量X的分布列;
(4)由期望、方差的定义求E(X),D(X).
特别地,若随机变量服从两点分布或二项分布,可根据公式直接计算E(X)和D(X).
