第2章 正态分布章末复习提升
图片预览











文档简介
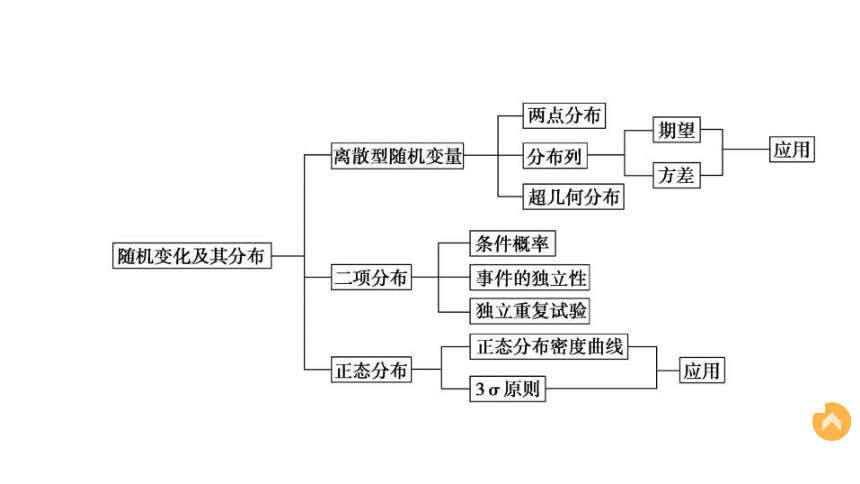
课件53张PPT。第二章——概 率1知识网络 系统盘点,提炼主干2要点归纳 整合要点,诠释疑点3题型研修 突破重点,提升能力章末复习提升1.离散型随机变量及其分布列
(1)随机变量:在随机试验中,我们确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果的变化而变化.像这种随着试验结果变化而变化的变量称为随机变量.通常用字母X,Y,ξ,η,…等表示.(2)离散型随机变量:所有取值可以一一列出的随机变量称为离散型随机变量.
(3)离散型随机变量的分布列:
一般地,若离散型随机变量X可能取的不同值为x1,x2…,xi,…xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=Pi,以表格的形式表示如下:我们将上表称为离散型随机变量X的概率分布列,简称为X的分布列.有时为了简单起见,也用等式P(X=xi)=Pi,i=1,2,…,n表示X的分布列.(4)离散型随机变量的分布列的性质:
①Pi≥0,i=1,2,…,n;
②P1+P2+…+Pn=1.
(5)常见的分布列:
两点分布:如果随机变量X的分布列
具有下表的形式,则称X服从两点分
布,并称P=P(X=1)为成功概率.两点分布又称0-1分布,伯努利分布.
超几何分布:一般地,设有总数为N件的两类物品,其中一类有M件,从所有物品中任取n件(n≤N),这n件中所含这类物品件数X是一个离散型随机变量,它取值为m时的概率为P(X=m)= (0≤m≤l,l为n和M中较小的一个),则称离散型随机变量X的这种形式的概率分布为超几何分布,也称X服从参数为N,M,n的超几何分布.2.二项分布及其应用
(1)条件概率:一般地,设A和B是两个事件,且P(A)>0,称P(B|A)= 为在事件A发生的条件下,事件B发生的条件概率.P(B|A)读作A发生的条件下B发生的概率.
(2)条件概率的性质:
①0≤P(B|A)≤1;
②必然事件的条件概率为1,不可能事件的条件概率为0;(4)独立重复试验:一般地,在相同条件下重复做的n次试验称为n次独立重复试验.
(5)二项分布:一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为P,那么在n次独立重复试验中,事件A恰好发生k次的概率为P(X=k)=
C Pk(1-P)n-k,k=0,1,2,…,n.此时称随机变量X服从二项分布,记作X~B(n,P),并称P为成功概率.两点分布是当n=1时的二项分布,二项分布可以看成是两点分布的一般形式.3.离散型随机变量的均值与方差
(1)均值、方差:一般地,若离散型随机变量X的分布列为则称E(X)=x1P1+x2P2+…+xiPi+…+xnPn为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.(2)均值与方差的性质:若Y=aX+b,其中a,b是常数,X是随机变量,则Y也是随机变量,且E(aX+b)=aE(X)+b,D(aX+b)=a2D(X).
(3)常见分布的均值和方差公式:①两点分布:若随机变量X服从参数为P的两点分布,则均值E(X)=P,方差D(X)=P(1-P).
②二项分布:若随机变量X~B(n,P),则均值E(X)=nP,方差D(X)=nP(1-P).4.正态分布
(1)正态曲线与正态分布:
①正态曲线:我们把函数f(x)= ,x∈(-∞,+∞)(其中μ是样本均值,σ是样本标准差)的图象称为正态分布密度曲线,简称正态曲线,正态曲线呈钟形,即中间高,两边低.②正态分布:一般地,如果对于任何实数a,b(a<b),随机变量X满足P(a<X≤b)= f(x)dx,则称随机变量X服从正态分布.正态分布完全由参数μ,σ确定,因此正态分布常记作N(μ,σ2).(2)正态曲线的特点:
①曲线位于x轴上方,与x轴不相交;
②曲线是单峰的,它关于直线x=μ对称;
③曲线在x=μ处达到峰值 ;
④曲线与x轴之间的面积为1.(3)μ和σ对正态曲线的影响:
①当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移;
②当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.(4)正态分布的3σ原则:若随机变量X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=68.3%,P(μ-2σ<X≤μ+2σ)=95.4%,P(μ-3σ<X≤μ+3σ)=99.7%.在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值,并简称之为3σ原则. 题型一 条件概率的求法
求条件概率的主要方法:(1)利用条件概率:P(B|A)= .
(2)针对古典概型,缩减基本事件总数P(B|A)= .例1 坛子里放着7个大小、形状相同的鸭蛋,其中有4个是绿皮的,3个是白皮的.如果不放回地依次拿出2个鸭蛋,求:
(1)第1次拿出绿皮鸭蛋的概率;
解 设“第1次拿出绿皮鸭蛋”为事件A,
“第2次拿出绿皮鸭蛋”为事件B,
则“第1次和第2次都拿出绿皮鸭蛋”为事件AB.(2)第1次和第2次都拿出绿皮鸭蛋的概率;(3)在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.
解 方法一 由(1)(2)可得,在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率为方法二 因为n(AB)=12,n(A)=24,跟踪演练1 一个盒子装有4只产品,其中有3只一等品、1只二等品,从中取产品两次,每次任取一只,作不放回抽样,设事件A为“第一次取到的是一等品”,事件B为“第二次取到的是一等品”,试求条件概率P(B|A).
解 将产品编号1,2,3号为一等品,4号为二等品,以(i,j)表示第一次,第二次分别取到第i号、第j号产品,则试验的样本空间为Ω={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2).(3,4),(4,1),(4,2),(4,3)},A={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4)},
AB={(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)},题型二 互斥事件、相互独立事件的概率
求概率的问题往往可以先转化为互斥事件概率的和,再运用相互独立事件的概率公式求解.例2 国家射击队为备战2016年里约热内卢奥运会进行紧张艰苦的训练,训练项目完成后,教练总会设计安排一些放松、娱乐性恢复活动.在一次速射“飞碟”的游戏活动中,教练制定如下规则:每次飞碟飞行过程中只允许射击三次,根据飞碟飞行的规律,队员甲在飞行距离为50米远处第一次射击命中的概率为 .(1)如果队员甲一共参加了三次射击飞碟的游戏,试求队员甲在这三次游戏中第一次至少有一次击中的概率;
解 记“队员甲在三次游戏中,第一次至少有一次命中”为事件A.(2)如果队员甲射击飞行距离为50米远处的飞碟,如果第一次未命中,则进行第二次射击,同时第二次射击时飞碟飞行距离变为100米;如果第二次未命中,则进行第三次射击,第三次射击时飞碟飞行距离变为150米(此后飞碟不在射程之内).已知,命中的概率与飞碟飞行距离的平方成反比,求队员甲在一次游戏中命中飞碟的概率.解 记“在一次游戏中,第i次击中飞碟”为事件Bi(i=1,2,3).又Bi是相互独立事件,跟踪演练2 甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响,求前三局比赛甲队领先的概率.
解 单局比赛甲队胜乙队的概率为0.6,乙队胜甲队的概率为1-0.6=0.4,
记“甲队胜三局”为事件A,
“甲队胜二局”为事件B,则:∴前三局比赛甲队领先的概率为P(A)+P(B)=0.648.题型三 离散型随机变量的分布列、期望与方差
离散型随机变量的分布列是研究随机变量的期望和方差的基础,利用分布列还可以求随机变量在某个范围内取值的概率.例3 甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是 ,假设各局比赛结果相互独立.(1)分别求甲队以3∶0,3∶1,3∶2胜利的概率;
解 记“甲队以3∶0胜利”为事件A1,
“甲队以3∶1胜利”为事件A2,
“甲队以3∶2胜利”为事件A3,
由题意,各局比赛结果相互独立, (2)若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列及数学期望.
解 设“乙队以3∶2胜利”为事件A4,由题意,各局比赛结果相互独立,所以
由题意,随机变量X的所有可能的取值为0,1,2,3,,根据事件的互斥性得故X的分布列为跟踪演练3 口袋里装有大小相同的卡片8张,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取一张,放回口袋后,第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为ξ.求ξ的期望.
解 依题意,随机变量ξ的取值是2,3,4,5,6.∴ξ的分布列是题型四 正态分布的应用
例4 某地数学考试的成绩X服从正态分布,某密度函数曲线如下图所示,成绩X位于区间(52,68]的概率为多少?解 设成绩X~N(μ,σ2),
则正态分布的密度函数∴P(52结合图象可知μ=8 000,σ=500.
(1)此地农民工年均收入的正态分布密度函数表达式为(2)求此地农民工年均收入在8 000~8 500元之间的人数百分比.
解 ∵P(7 500<ξ≤8 500)
=P(8 000-500<ξ≤8 000+500)
=68.3%.
∴P(8 000<ξ≤8 500)=34.15%.即农民工年均收入在8 000~8 500之间的人数占总体的34.15%.课堂小结
本章通过引入随机变量的概念,研究了几种类型的随机变量的分布列,以及条件概率、事件的独立性及相互独立的事件同时发生的概率公式.通过研究随机变量的数字特征如均值(数学期望)和方差(或标准差),以及随机变量的分布列,对随机变量的总体水平及稳定程度进行了刻画,并通过样本均值和方差(或标准差)对总体进行估计.超几何分布、二项分布、n重独立重复试验及正态分布等,都是重要的概率模型,在社会生产、生活和科学研究中有着广泛的应用.
(1)随机变量:在随机试验中,我们确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果的变化而变化.像这种随着试验结果变化而变化的变量称为随机变量.通常用字母X,Y,ξ,η,…等表示.(2)离散型随机变量:所有取值可以一一列出的随机变量称为离散型随机变量.
(3)离散型随机变量的分布列:
一般地,若离散型随机变量X可能取的不同值为x1,x2…,xi,…xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=Pi,以表格的形式表示如下:我们将上表称为离散型随机变量X的概率分布列,简称为X的分布列.有时为了简单起见,也用等式P(X=xi)=Pi,i=1,2,…,n表示X的分布列.(4)离散型随机变量的分布列的性质:
①Pi≥0,i=1,2,…,n;
②P1+P2+…+Pn=1.
(5)常见的分布列:
两点分布:如果随机变量X的分布列
具有下表的形式,则称X服从两点分
布,并称P=P(X=1)为成功概率.两点分布又称0-1分布,伯努利分布.
超几何分布:一般地,设有总数为N件的两类物品,其中一类有M件,从所有物品中任取n件(n≤N),这n件中所含这类物品件数X是一个离散型随机变量,它取值为m时的概率为P(X=m)= (0≤m≤l,l为n和M中较小的一个),则称离散型随机变量X的这种形式的概率分布为超几何分布,也称X服从参数为N,M,n的超几何分布.2.二项分布及其应用
(1)条件概率:一般地,设A和B是两个事件,且P(A)>0,称P(B|A)= 为在事件A发生的条件下,事件B发生的条件概率.P(B|A)读作A发生的条件下B发生的概率.
(2)条件概率的性质:
①0≤P(B|A)≤1;
②必然事件的条件概率为1,不可能事件的条件概率为0;(4)独立重复试验:一般地,在相同条件下重复做的n次试验称为n次独立重复试验.
(5)二项分布:一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为P,那么在n次独立重复试验中,事件A恰好发生k次的概率为P(X=k)=
C Pk(1-P)n-k,k=0,1,2,…,n.此时称随机变量X服从二项分布,记作X~B(n,P),并称P为成功概率.两点分布是当n=1时的二项分布,二项分布可以看成是两点分布的一般形式.3.离散型随机变量的均值与方差
(1)均值、方差:一般地,若离散型随机变量X的分布列为则称E(X)=x1P1+x2P2+…+xiPi+…+xnPn为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.(2)均值与方差的性质:若Y=aX+b,其中a,b是常数,X是随机变量,则Y也是随机变量,且E(aX+b)=aE(X)+b,D(aX+b)=a2D(X).
(3)常见分布的均值和方差公式:①两点分布:若随机变量X服从参数为P的两点分布,则均值E(X)=P,方差D(X)=P(1-P).
②二项分布:若随机变量X~B(n,P),则均值E(X)=nP,方差D(X)=nP(1-P).4.正态分布
(1)正态曲线与正态分布:
①正态曲线:我们把函数f(x)= ,x∈(-∞,+∞)(其中μ是样本均值,σ是样本标准差)的图象称为正态分布密度曲线,简称正态曲线,正态曲线呈钟形,即中间高,两边低.②正态分布:一般地,如果对于任何实数a,b(a<b),随机变量X满足P(a<X≤b)= f(x)dx,则称随机变量X服从正态分布.正态分布完全由参数μ,σ确定,因此正态分布常记作N(μ,σ2).(2)正态曲线的特点:
①曲线位于x轴上方,与x轴不相交;
②曲线是单峰的,它关于直线x=μ对称;
③曲线在x=μ处达到峰值 ;
④曲线与x轴之间的面积为1.(3)μ和σ对正态曲线的影响:
①当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移;
②当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.(4)正态分布的3σ原则:若随机变量X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=68.3%,P(μ-2σ<X≤μ+2σ)=95.4%,P(μ-3σ<X≤μ+3σ)=99.7%.在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值,并简称之为3σ原则. 题型一 条件概率的求法
求条件概率的主要方法:(1)利用条件概率:P(B|A)= .
(2)针对古典概型,缩减基本事件总数P(B|A)= .例1 坛子里放着7个大小、形状相同的鸭蛋,其中有4个是绿皮的,3个是白皮的.如果不放回地依次拿出2个鸭蛋,求:
(1)第1次拿出绿皮鸭蛋的概率;
解 设“第1次拿出绿皮鸭蛋”为事件A,
“第2次拿出绿皮鸭蛋”为事件B,
则“第1次和第2次都拿出绿皮鸭蛋”为事件AB.(2)第1次和第2次都拿出绿皮鸭蛋的概率;(3)在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.
解 方法一 由(1)(2)可得,在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率为方法二 因为n(AB)=12,n(A)=24,跟踪演练1 一个盒子装有4只产品,其中有3只一等品、1只二等品,从中取产品两次,每次任取一只,作不放回抽样,设事件A为“第一次取到的是一等品”,事件B为“第二次取到的是一等品”,试求条件概率P(B|A).
解 将产品编号1,2,3号为一等品,4号为二等品,以(i,j)表示第一次,第二次分别取到第i号、第j号产品,则试验的样本空间为Ω={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2).(3,4),(4,1),(4,2),(4,3)},A={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4)},
AB={(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)},题型二 互斥事件、相互独立事件的概率
求概率的问题往往可以先转化为互斥事件概率的和,再运用相互独立事件的概率公式求解.例2 国家射击队为备战2016年里约热内卢奥运会进行紧张艰苦的训练,训练项目完成后,教练总会设计安排一些放松、娱乐性恢复活动.在一次速射“飞碟”的游戏活动中,教练制定如下规则:每次飞碟飞行过程中只允许射击三次,根据飞碟飞行的规律,队员甲在飞行距离为50米远处第一次射击命中的概率为 .(1)如果队员甲一共参加了三次射击飞碟的游戏,试求队员甲在这三次游戏中第一次至少有一次击中的概率;
解 记“队员甲在三次游戏中,第一次至少有一次命中”为事件A.(2)如果队员甲射击飞行距离为50米远处的飞碟,如果第一次未命中,则进行第二次射击,同时第二次射击时飞碟飞行距离变为100米;如果第二次未命中,则进行第三次射击,第三次射击时飞碟飞行距离变为150米(此后飞碟不在射程之内).已知,命中的概率与飞碟飞行距离的平方成反比,求队员甲在一次游戏中命中飞碟的概率.解 记“在一次游戏中,第i次击中飞碟”为事件Bi(i=1,2,3).又Bi是相互独立事件,跟踪演练2 甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响,求前三局比赛甲队领先的概率.
解 单局比赛甲队胜乙队的概率为0.6,乙队胜甲队的概率为1-0.6=0.4,
记“甲队胜三局”为事件A,
“甲队胜二局”为事件B,则:∴前三局比赛甲队领先的概率为P(A)+P(B)=0.648.题型三 离散型随机变量的分布列、期望与方差
离散型随机变量的分布列是研究随机变量的期望和方差的基础,利用分布列还可以求随机变量在某个范围内取值的概率.例3 甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是 ,假设各局比赛结果相互独立.(1)分别求甲队以3∶0,3∶1,3∶2胜利的概率;
解 记“甲队以3∶0胜利”为事件A1,
“甲队以3∶1胜利”为事件A2,
“甲队以3∶2胜利”为事件A3,
由题意,各局比赛结果相互独立, (2)若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列及数学期望.
解 设“乙队以3∶2胜利”为事件A4,由题意,各局比赛结果相互独立,所以
由题意,随机变量X的所有可能的取值为0,1,2,3,,根据事件的互斥性得故X的分布列为跟踪演练3 口袋里装有大小相同的卡片8张,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取一张,放回口袋后,第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为ξ.求ξ的期望.
解 依题意,随机变量ξ的取值是2,3,4,5,6.∴ξ的分布列是题型四 正态分布的应用
例4 某地数学考试的成绩X服从正态分布,某密度函数曲线如下图所示,成绩X位于区间(52,68]的概率为多少?解 设成绩X~N(μ,σ2),
则正态分布的密度函数∴P(52
(1)此地农民工年均收入的正态分布密度函数表达式为(2)求此地农民工年均收入在8 000~8 500元之间的人数百分比.
解 ∵P(7 500<ξ≤8 500)
=P(8 000-500<ξ≤8 000+500)
=68.3%.
∴P(8 000<ξ≤8 500)=34.15%.即农民工年均收入在8 000~8 500之间的人数占总体的34.15%.课堂小结
本章通过引入随机变量的概念,研究了几种类型的随机变量的分布列,以及条件概率、事件的独立性及相互独立的事件同时发生的概率公式.通过研究随机变量的数字特征如均值(数学期望)和方差(或标准差),以及随机变量的分布列,对随机变量的总体水平及稳定程度进行了刻画,并通过样本均值和方差(或标准差)对总体进行估计.超几何分布、二项分布、n重独立重复试验及正态分布等,都是重要的概率模型,在社会生产、生活和科学研究中有着广泛的应用.
