第3章 3.1 独立性检验
图片预览











文档简介
课件35张PPT。第三章——统计案例3.1 独立性检验[学习目标]
1.理解列联表的意义,会根据列联表中数据大致判断两个变量是否独立.
2.理解统计量χ2的意义和独立性检验的基本思想.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.什么是列联表,它有什么作用?
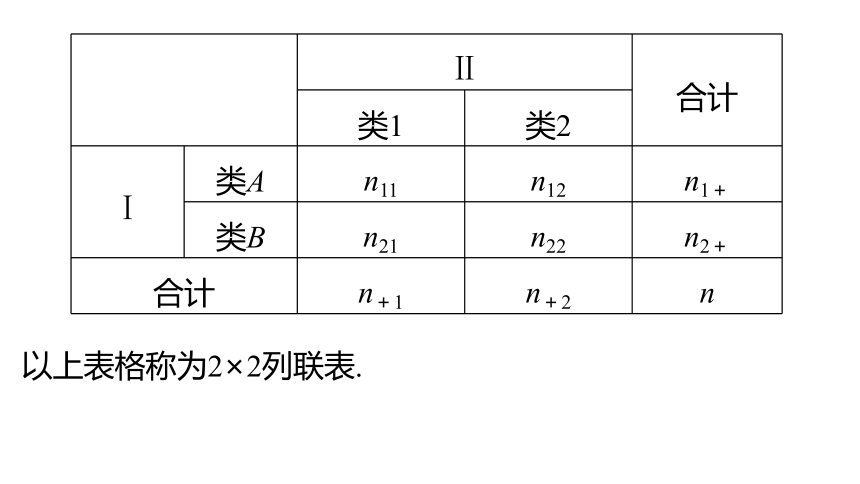
答 一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值类A和类B,Ⅱ也有两类取值类1和类2,得如下列联表中的抽样数据:以上表格称为2×2列联表.2.统计量χ2有什么作用?[预习导引]
1.2×2列联表:
一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值类A和类B,Ⅱ也有两类取值类1和类2,得到如下列联表所示的抽样数据:上述表格称为2×2列联表.3.独立性检验
要推断“Ⅰ与Ⅱ有关系”,可按下面的步骤进行:
(1)提出假设H0: ;(2)根据2×2列联表计算__的值;(3)查对临界值,作出判断.Ⅰ与Ⅱ没有关系χ2要点一 2×2列联表和χ2统计量
例1 根据下表计算:
χ2≈________.(结果保留3位小数)答案 4.514规律方法 利用χ2= ,准确代数与计算,求出χ2的值.跟踪演练1 已知列联表:药物效果与动物试验列联表则χ2≈________.(结果保留3位小数)答案 6.109要点二 有关“相关的检验”
例2 某校对学生课外活动进行调查,结果整理成下表:
用你所学过的知识进行分析,能否在犯错误的概率不超过0.01的前提下,认为“喜欢体育还是文娱与性别有关系”?解 判断方法如下:
假设H0“喜欢体育还是喜欢文娱与性别没有关系”,若H0成立,则χ2应该很小.
∵n11=21,n12=23,n21=6,n22=29,n=79,∵χ2≥6.635,
∴我们有99%的把握认为“喜欢体育还是文娱与性别有关系”,
即在犯错误的概率不超过0.01的前提下认为“喜欢体育还是喜欢文娱与性别有关”.规律方法 (1)利用χ2= 求出χ2的值.再利用临界值的大小来判断假设是否成立.
(2)解题时应注意准确代数与计算,不可错用公式,准确进行比较与判断.跟踪演练2 为了研究人的性别与患色盲是否有关系,某研究所进行了随机调查,发现在调查的480名男性中有39名患有色盲,520名女性中有6名患有色盲,能在犯错误的概率不超过0.01的前提下认为人的性别与患色盲有关系吗?
解 由题意列出2×2列联表:因为χ2≥6.635,所以有99%的把握认为人的性别与患色盲有关系,即在犯错误的概率不超过0.01的前提下认为患色盲与人的性别有关系,男性患色盲的概率要比女性大得多要点三 有关“无关的检验”
例3 为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?解 列出2×2列联表∵1.871×10-4≤3.841,可以认为学生选报文、理科与对外语的兴趣无关.规律方法 运用独立性检验的方法:
1.列出2×2列联表,根据公式计算χ2.
2.根据临界值作出判断.跟踪演练3 调查在2~3级风的海上航行中男女乘客的晕船情况,结果如下表所示:根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?解 假设H0:海上航行和性别没有关系,因为χ2<3.841,所以我们没有理由认为男人比女人更容易晕船.12341.当χ2>3.841时,认为事件A与事件B( )
A.有95%的把握有关
B.有99%的把握有关
C.没有理由说它们有关
D.不确定A12342.为了考察中学生的性别与是否喜欢数学课程之间的关系,在某校中学生中随机抽取了300名学生,得到如下列联表:1234你认为性别与是否喜欢数学课程之间有关系的把握有( )
A.0 B.95%
C.99% D.100%B3.某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集哪些数据?
_________________________________________________________.1234女正教授人数、男正教授人数、女副教授人数、男副教授人数4.为研究学生的数学成绩与对学习数学的兴趣是否有关,对某年级学生作调查,得到如下数据:1234学生的数学成绩好坏与对学习数学的兴趣是否有关?1234∵38.459>6.635,
∴有99%的把握说,学生学习数学的兴趣与数学成绩是有关的.课堂小结
1.独立性检验的思想:先假设两个事件无关,计算统计量χ2的值.若χ2值较大,则拒绝假设,认为两个事件有关,若χ2值较小,则假设成立,认为两个事件无关.
2.独立性检验的步骤:(1)作出假设H0:Ⅰ与Ⅱ没有关系;
(2)计算χ2的值;(3)和临界值比较作出判断.
1.理解列联表的意义,会根据列联表中数据大致判断两个变量是否独立.
2.理解统计量χ2的意义和独立性检验的基本思想.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.什么是列联表,它有什么作用?
答 一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值类A和类B,Ⅱ也有两类取值类1和类2,得如下列联表中的抽样数据:以上表格称为2×2列联表.2.统计量χ2有什么作用?[预习导引]
1.2×2列联表:
一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值类A和类B,Ⅱ也有两类取值类1和类2,得到如下列联表所示的抽样数据:上述表格称为2×2列联表.3.独立性检验
要推断“Ⅰ与Ⅱ有关系”,可按下面的步骤进行:
(1)提出假设H0: ;(2)根据2×2列联表计算__的值;(3)查对临界值,作出判断.Ⅰ与Ⅱ没有关系χ2要点一 2×2列联表和χ2统计量
例1 根据下表计算:
χ2≈________.(结果保留3位小数)答案 4.514规律方法 利用χ2= ,准确代数与计算,求出χ2的值.跟踪演练1 已知列联表:药物效果与动物试验列联表则χ2≈________.(结果保留3位小数)答案 6.109要点二 有关“相关的检验”
例2 某校对学生课外活动进行调查,结果整理成下表:
用你所学过的知识进行分析,能否在犯错误的概率不超过0.01的前提下,认为“喜欢体育还是文娱与性别有关系”?解 判断方法如下:
假设H0“喜欢体育还是喜欢文娱与性别没有关系”,若H0成立,则χ2应该很小.
∵n11=21,n12=23,n21=6,n22=29,n=79,∵χ2≥6.635,
∴我们有99%的把握认为“喜欢体育还是文娱与性别有关系”,
即在犯错误的概率不超过0.01的前提下认为“喜欢体育还是喜欢文娱与性别有关”.规律方法 (1)利用χ2= 求出χ2的值.再利用临界值的大小来判断假设是否成立.
(2)解题时应注意准确代数与计算,不可错用公式,准确进行比较与判断.跟踪演练2 为了研究人的性别与患色盲是否有关系,某研究所进行了随机调查,发现在调查的480名男性中有39名患有色盲,520名女性中有6名患有色盲,能在犯错误的概率不超过0.01的前提下认为人的性别与患色盲有关系吗?
解 由题意列出2×2列联表:因为χ2≥6.635,所以有99%的把握认为人的性别与患色盲有关系,即在犯错误的概率不超过0.01的前提下认为患色盲与人的性别有关系,男性患色盲的概率要比女性大得多要点三 有关“无关的检验”
例3 为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?解 列出2×2列联表∵1.871×10-4≤3.841,可以认为学生选报文、理科与对外语的兴趣无关.规律方法 运用独立性检验的方法:
1.列出2×2列联表,根据公式计算χ2.
2.根据临界值作出判断.跟踪演练3 调查在2~3级风的海上航行中男女乘客的晕船情况,结果如下表所示:根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?解 假设H0:海上航行和性别没有关系,因为χ2<3.841,所以我们没有理由认为男人比女人更容易晕船.12341.当χ2>3.841时,认为事件A与事件B( )
A.有95%的把握有关
B.有99%的把握有关
C.没有理由说它们有关
D.不确定A12342.为了考察中学生的性别与是否喜欢数学课程之间的关系,在某校中学生中随机抽取了300名学生,得到如下列联表:1234你认为性别与是否喜欢数学课程之间有关系的把握有( )
A.0 B.95%
C.99% D.100%B3.某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集哪些数据?
_________________________________________________________.1234女正教授人数、男正教授人数、女副教授人数、男副教授人数4.为研究学生的数学成绩与对学习数学的兴趣是否有关,对某年级学生作调查,得到如下数据:1234学生的数学成绩好坏与对学习数学的兴趣是否有关?1234∵38.459>6.635,
∴有99%的把握说,学生学习数学的兴趣与数学成绩是有关的.课堂小结
1.独立性检验的思想:先假设两个事件无关,计算统计量χ2的值.若χ2值较大,则拒绝假设,认为两个事件有关,若χ2值较小,则假设成立,认为两个事件无关.
2.独立性检验的步骤:(1)作出假设H0:Ⅰ与Ⅱ没有关系;
(2)计算χ2的值;(3)和临界值比较作出判断.
