第3章 3.2 回归分析
图片预览











文档简介
课件60张PPT。第三章——统计案例3.2 回归分析[学习目标]
1.会建立线性回归模型分析两个变量间的相关关系.
2.能通过相关系数判断两个变量间的线性相关程度.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.什么叫回归分析?
答 回归分析是对具有相关关系的两个变量进行统计分析的一种方法.2.回归分析中,利用线性回归方程求出的函数值一定是真实值吗?
答 不一定是真实值,利用线性回归方程求的值,在很多时候是个预报值,例如,人的体重与身高存在一定的线性关系,但体重除了受身高的影响外,还受其他因素的影响,如饮食、是否喜欢运动等.[预习导引]2.相关系数
对于变量x与y随机抽到的n对数据(x1,y1),(x2,y2),…,(xn,yn),检测统计量是样本相关系数相关系数r的取值范围是 ,|r|越接近1,变量之间的线性相关程度越高,|r|越接近0,线性相关程度越弱,当|r|>
时,有95%的把握认为两个变量之间有线性相关关系.[-1,1]r0.053.非线性回归分析
回归曲线方程也可以线性化
(1)将幂函数型函数y=axn(a为常数,a,x,y均取正值)化为线性函数:
将y=axn两边取常用对数,则有lg y=nlg x+lg a,令μ=lg y,v=lg x,b=lg a,代入上式得μ=nv+b(其中n、b是常数),其图象是一条直线.(2)将指数型函数y=cax(a>0,c>0,a,c为常数)化为线性函数;
将y=cax两边取常用对数,则有lg y=xlg a+lg c,令μ=lg y,b=lg c,d=lg a,代入上式得μ=dx+b(d,b是常数),它的图象是一条直线.要点一 求线性回归方程
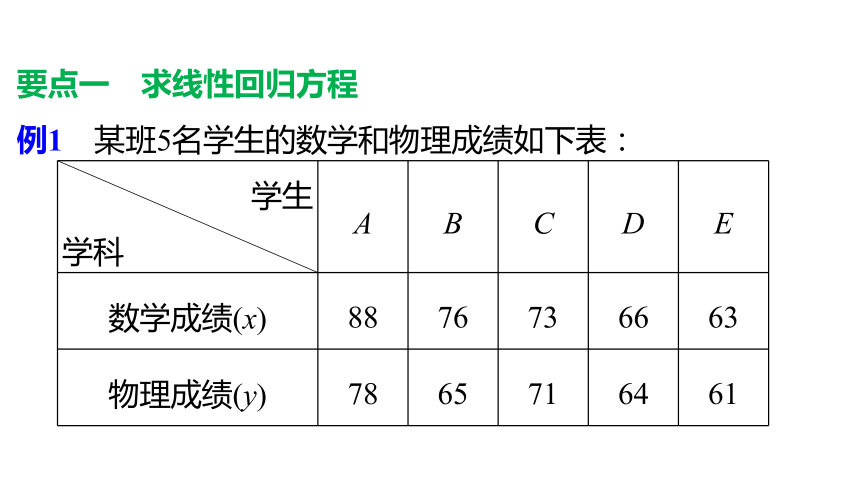
例1 某班5名学生的数学和物理成绩如下表:(1)画出散点图;
解 散点图如图.(2)求物理成绩y对数学成绩x的回归直线方程;(3)一名学生的数学成绩是96,试预测他的物理成绩.
即可以预测他的物理成绩是82.规律方法 (1)散点图是定义在具有相关关系的两个变量基础上的,对于性质不明确的两组数据,可先作散点图,在图上看它们有无关系,关系的密切程度,然后再进行相关回归分析.
(2)求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.跟踪演练1 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:(1)请画出上表数据的散点图(要求:点要描粗);
解 如图:(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.要点二 相关性检验
例2 下面的数据是从年龄在40到60岁的男子中随机抽出的6个样本,分别测定了心脏的功能水平y(满分100)以及每天花在看电视上的平均时间x(小时).(1)求心脏的功能水平y与每天花在看电视上的平均时间x之间的样本相关系数r;心脏的功能水平y与每天花在看电视上的平均时间x之间的相关系数(2)求心脏的功能水平y与每天花在看电视上的平均时间x的线性回归方程,并讨论方程是否有意义;查表n-2=4,r0.05=0.811,因为|r|≈0.902 5>0.811,
所以有95%以上的把握认为y与x之间有线性关系,这个方程是有意义的.(3)估计平均每天看电视3小时的男子的心脏的功能水平.因此估计平均每天看电视3小时的男子的心脏的功能水平为69分.规律方法 解决这一类问题时,首先应对问题进行必要的相关性检验,如果不作相关性检验,我们仍然可以求出x与y的线性回归方程,但不知道这时的线性回归方程是否有意义,也就不知道能否反映变量x与y之间的变化规律,只有在x与y之间具有相关关系时,求得的线性回归方程才有意义.跟踪演练2 维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量,这个指标越高,耐热水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x(g/L)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据.(1)画散点图;
解 (2)求线性回归方程;
解 列表:=0.264 3,(3)求相关系数r,并进行相关性检验.=0.96.
计算得r=0.96>r0.05=0.754.说明甲醛浓度与缩醛化度两个变量之间有较强的线性相关关系.要点三 非线性回归模型
例3 某地区不同身高的未成年男性的体重平均值如下表:试建立y与x之间的回归方程.解 根据上表中数据画出散点图如图所示.由图看出,样本点分布在某条指数型函数曲线y=c1e 的周围,于是令z=ln y.由计算器计算可得下表,c2x画出散点图如图所示.由表中数据可得z与x之间的回归直线方程:规律方法 根据已有的函数知识,可以发现样本分布在某一条指数型函数曲线y=c1e 的周围,其中c1和c2是待定参数;可以通过对x进行对数变换,转化为线性相关关系.c2x跟踪演练3 某种书每册的成本费Y(元)与印刷册数x(千册)有关,经统计得到数据如下:检验每册书的成本费Y与印刷册数的倒数 之间是否具有线性相关关系?若有,求出Y对x的回归方程;若无,说明理由.解 设μ=,则Y与μ的数据关系如下表所示:经过计算r=0.999 8>r0.05=0.632.
从而有95%的把握认为这两个变量具有线性相关关系,从而求Y与μ的回归直线方程有意义.1.下列各组变量之间具有线性相关关系的是( )
A.出租车费与行驶的里程
B.学习成绩与学生身高
C.身高与体重
D.铁的体积与质量1234C12342.若劳动生产率x(千元)与月工资y(元)之间的线性回归方程为
=50+80x,则下列判断正确的是( )
A.劳动生产率为1 000元时,月工资为130元
B.劳动生产率提高1 000元时,月工资平均提高80元
C.劳动生产率提高1 000元时,月工资平均提高130元
D.月工资为210元时,劳动生产率为2 000元B12341234解析 由于销售量y与销售价格x成负相关,故排除B、D.
又当x=10时,A中y=100,而C中y=-300,C不符合实际情况,故选A.
答案 A4.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:12341234(1)求年推销金额y关于工作年限x的线性回归方程;12341234(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.所以可以估计第6名推销员的年推销金额为5.9万元.课堂小结
回归分析的基本思路:
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;
(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等);
1.会建立线性回归模型分析两个变量间的相关关系.
2.能通过相关系数判断两个变量间的线性相关程度.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.什么叫回归分析?
答 回归分析是对具有相关关系的两个变量进行统计分析的一种方法.2.回归分析中,利用线性回归方程求出的函数值一定是真实值吗?
答 不一定是真实值,利用线性回归方程求的值,在很多时候是个预报值,例如,人的体重与身高存在一定的线性关系,但体重除了受身高的影响外,还受其他因素的影响,如饮食、是否喜欢运动等.[预习导引]2.相关系数
对于变量x与y随机抽到的n对数据(x1,y1),(x2,y2),…,(xn,yn),检测统计量是样本相关系数相关系数r的取值范围是 ,|r|越接近1,变量之间的线性相关程度越高,|r|越接近0,线性相关程度越弱,当|r|>
时,有95%的把握认为两个变量之间有线性相关关系.[-1,1]r0.053.非线性回归分析
回归曲线方程也可以线性化
(1)将幂函数型函数y=axn(a为常数,a,x,y均取正值)化为线性函数:
将y=axn两边取常用对数,则有lg y=nlg x+lg a,令μ=lg y,v=lg x,b=lg a,代入上式得μ=nv+b(其中n、b是常数),其图象是一条直线.(2)将指数型函数y=cax(a>0,c>0,a,c为常数)化为线性函数;
将y=cax两边取常用对数,则有lg y=xlg a+lg c,令μ=lg y,b=lg c,d=lg a,代入上式得μ=dx+b(d,b是常数),它的图象是一条直线.要点一 求线性回归方程
例1 某班5名学生的数学和物理成绩如下表:(1)画出散点图;
解 散点图如图.(2)求物理成绩y对数学成绩x的回归直线方程;(3)一名学生的数学成绩是96,试预测他的物理成绩.
即可以预测他的物理成绩是82.规律方法 (1)散点图是定义在具有相关关系的两个变量基础上的,对于性质不明确的两组数据,可先作散点图,在图上看它们有无关系,关系的密切程度,然后再进行相关回归分析.
(2)求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.跟踪演练1 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:(1)请画出上表数据的散点图(要求:点要描粗);
解 如图:(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.要点二 相关性检验
例2 下面的数据是从年龄在40到60岁的男子中随机抽出的6个样本,分别测定了心脏的功能水平y(满分100)以及每天花在看电视上的平均时间x(小时).(1)求心脏的功能水平y与每天花在看电视上的平均时间x之间的样本相关系数r;心脏的功能水平y与每天花在看电视上的平均时间x之间的相关系数(2)求心脏的功能水平y与每天花在看电视上的平均时间x的线性回归方程,并讨论方程是否有意义;查表n-2=4,r0.05=0.811,因为|r|≈0.902 5>0.811,
所以有95%以上的把握认为y与x之间有线性关系,这个方程是有意义的.(3)估计平均每天看电视3小时的男子的心脏的功能水平.因此估计平均每天看电视3小时的男子的心脏的功能水平为69分.规律方法 解决这一类问题时,首先应对问题进行必要的相关性检验,如果不作相关性检验,我们仍然可以求出x与y的线性回归方程,但不知道这时的线性回归方程是否有意义,也就不知道能否反映变量x与y之间的变化规律,只有在x与y之间具有相关关系时,求得的线性回归方程才有意义.跟踪演练2 维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量,这个指标越高,耐热水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x(g/L)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据.(1)画散点图;
解 (2)求线性回归方程;
解 列表:=0.264 3,(3)求相关系数r,并进行相关性检验.=0.96.
计算得r=0.96>r0.05=0.754.说明甲醛浓度与缩醛化度两个变量之间有较强的线性相关关系.要点三 非线性回归模型
例3 某地区不同身高的未成年男性的体重平均值如下表:试建立y与x之间的回归方程.解 根据上表中数据画出散点图如图所示.由图看出,样本点分布在某条指数型函数曲线y=c1e 的周围,于是令z=ln y.由计算器计算可得下表,c2x画出散点图如图所示.由表中数据可得z与x之间的回归直线方程:规律方法 根据已有的函数知识,可以发现样本分布在某一条指数型函数曲线y=c1e 的周围,其中c1和c2是待定参数;可以通过对x进行对数变换,转化为线性相关关系.c2x跟踪演练3 某种书每册的成本费Y(元)与印刷册数x(千册)有关,经统计得到数据如下:检验每册书的成本费Y与印刷册数的倒数 之间是否具有线性相关关系?若有,求出Y对x的回归方程;若无,说明理由.解 设μ=,则Y与μ的数据关系如下表所示:经过计算r=0.999 8>r0.05=0.632.
从而有95%的把握认为这两个变量具有线性相关关系,从而求Y与μ的回归直线方程有意义.1.下列各组变量之间具有线性相关关系的是( )
A.出租车费与行驶的里程
B.学习成绩与学生身高
C.身高与体重
D.铁的体积与质量1234C12342.若劳动生产率x(千元)与月工资y(元)之间的线性回归方程为
=50+80x,则下列判断正确的是( )
A.劳动生产率为1 000元时,月工资为130元
B.劳动生产率提高1 000元时,月工资平均提高80元
C.劳动生产率提高1 000元时,月工资平均提高130元
D.月工资为210元时,劳动生产率为2 000元B12341234解析 由于销售量y与销售价格x成负相关,故排除B、D.
又当x=10时,A中y=100,而C中y=-300,C不符合实际情况,故选A.
答案 A4.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:12341234(1)求年推销金额y关于工作年限x的线性回归方程;12341234(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.所以可以估计第6名推销员的年推销金额为5.9万元.课堂小结
回归分析的基本思路:
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;
(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等);
