山东省聊城第三中学2019-2020学年九年级数学第一学期期中试卷及答案
文档属性
| 名称 | 山东省聊城第三中学2019-2020学年九年级数学第一学期期中试卷及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 16:43:31 | ||
图片预览

文档简介
2019-2020第一学期期中试卷
九年级数学
(时间100分钟,满分120分)
一、选择题(每小题3分,共36分)
1. 下列说法①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81,正确的有( )
A.1个 B.2个 C.3个 D.4个
2. 下列计算正确的是( )
A. B.
C. D.
3. 等腰直角三角形的外接圆半径等于( )
A.腰长 B.腰长的; C.底边的 D.腰上的高
4.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.ABM∽ACB B.ANC∽AMB C.ANC∽ACM D.CMN∽BCA
5.如图,沿折叠矩形纸片,使点落在边的点处.已知,,则的值为 ( )
A. B. C. D.
6.在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
A. B. C. D.
第4题 第5题 第6题
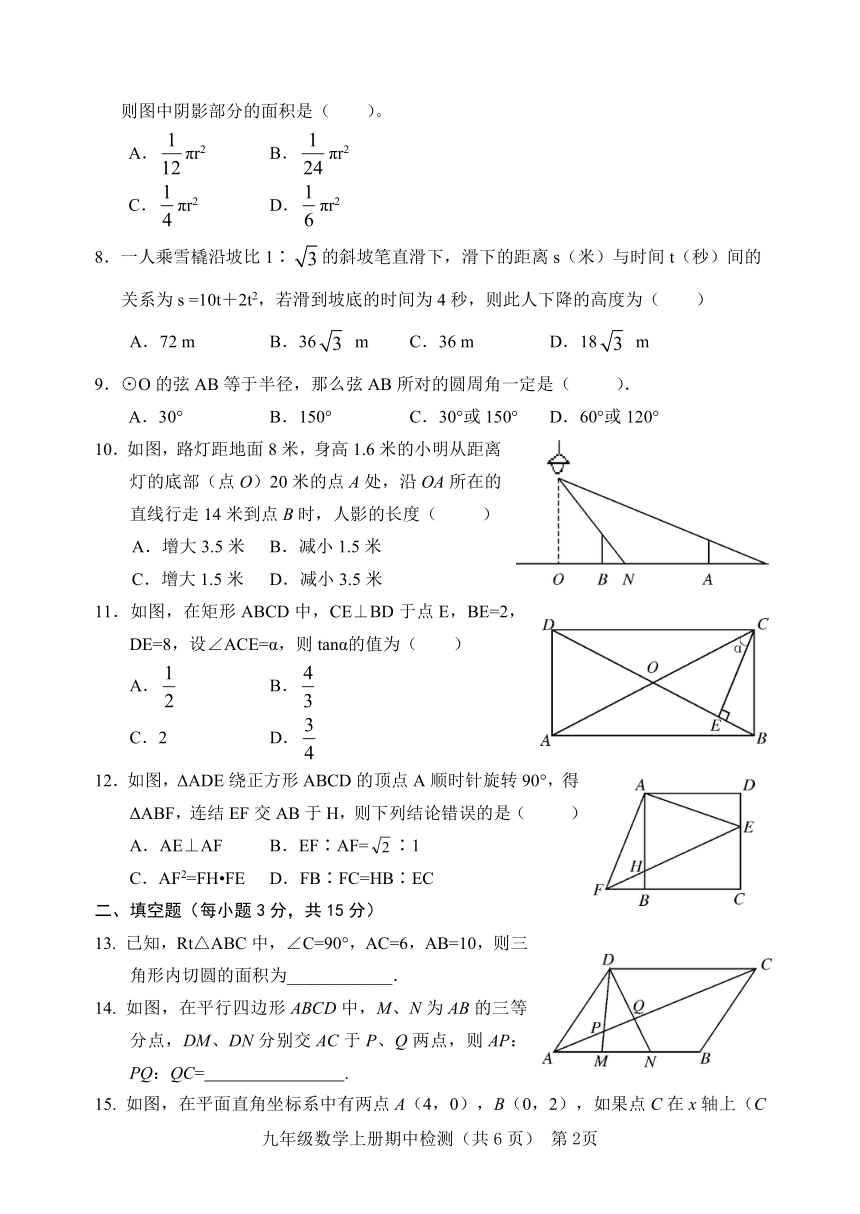
7.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )。
A.πr2 B.πr2
C.πr2 D.πr2
8.一人乘雪橇沿坡比1∶的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s =10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为( )
A.72 m B.36 m C.36 m D.18 m
9.⊙O的弦AB等于半径,那么弦AB所对的圆周角一定是( ).
A.30° B.150° C.30°或150° D.60°或120°
10.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大3.5米 B.减小1.5米
C.增大1.5米 D.减小3.5米
11.如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE=8,设∠ACE=α,则tanα的值为( )
A. B.
C.2 D.
12.如图,ΔADE绕正方形ABCD的顶点A顺时针旋转90°,得ΔABF,连结EF交AB于H,则下列结论错误的是( )
A.AE⊥AF B.EF∶AF=∶1
C.AF2=FH?FE D.FB∶FC=HB∶EC
二、填空题(每小题3分,共15分)
13. 已知,Rt△ABC中,∠C=90°,AC=6,AB=10,则三角形内切圆的面积为____________.
14. 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PQ:QC= .
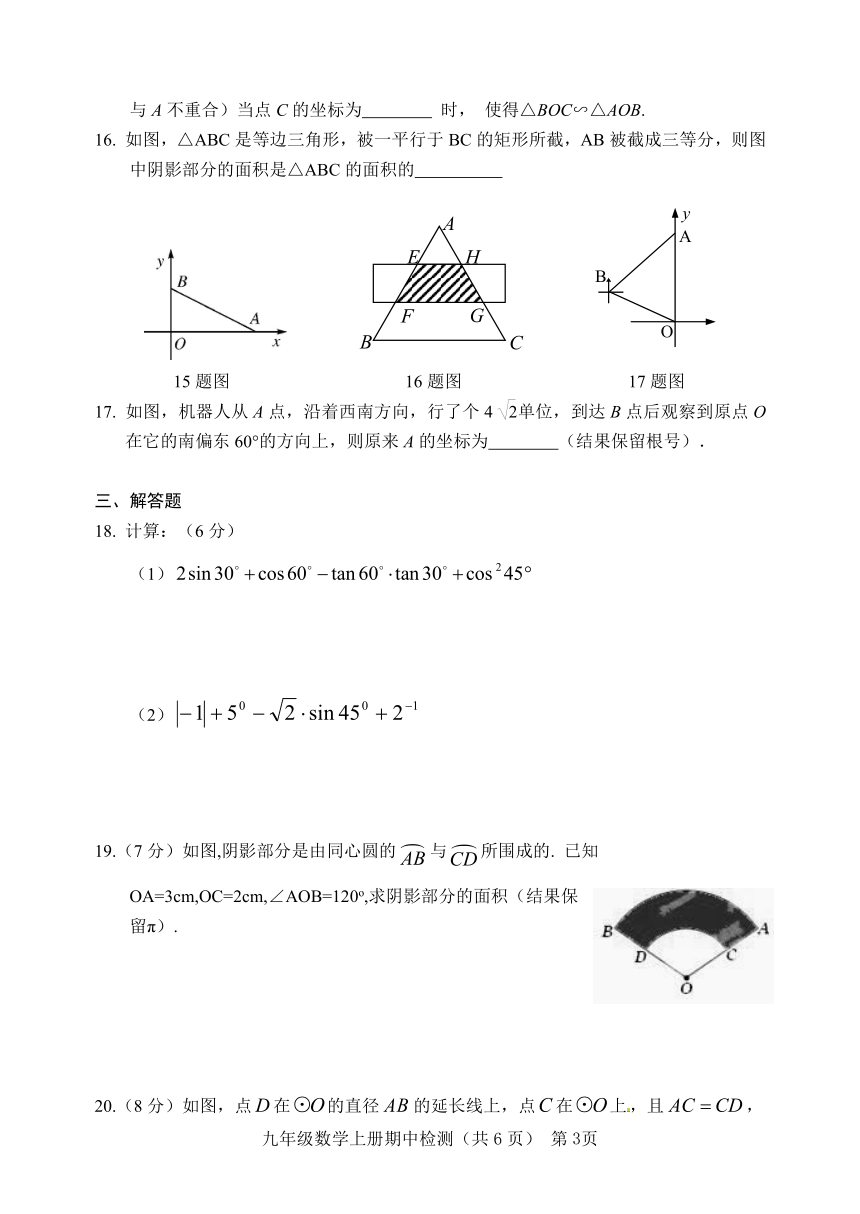
15. 如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为 ??时, 使得△BOC∽△AOB.
16. 如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的
15题图 16题图 17题图
17. 如图,机器人从A点,沿着西南方向,行了个4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为 (结果保留根号).
三、解答题
18. 计算:(6分)
(1)
(2) HYPERLINK "http://www.mathschina.com/Index.html"
19.(7分)如图,阴影部分是由同心圆的与所围成的. 已知OA=3cm,OC=2cm,∠AOB=120o,求阴影部分的面积(结果保留π).
20.(8分)如图,点在的直径的延长线上,点在上,且,
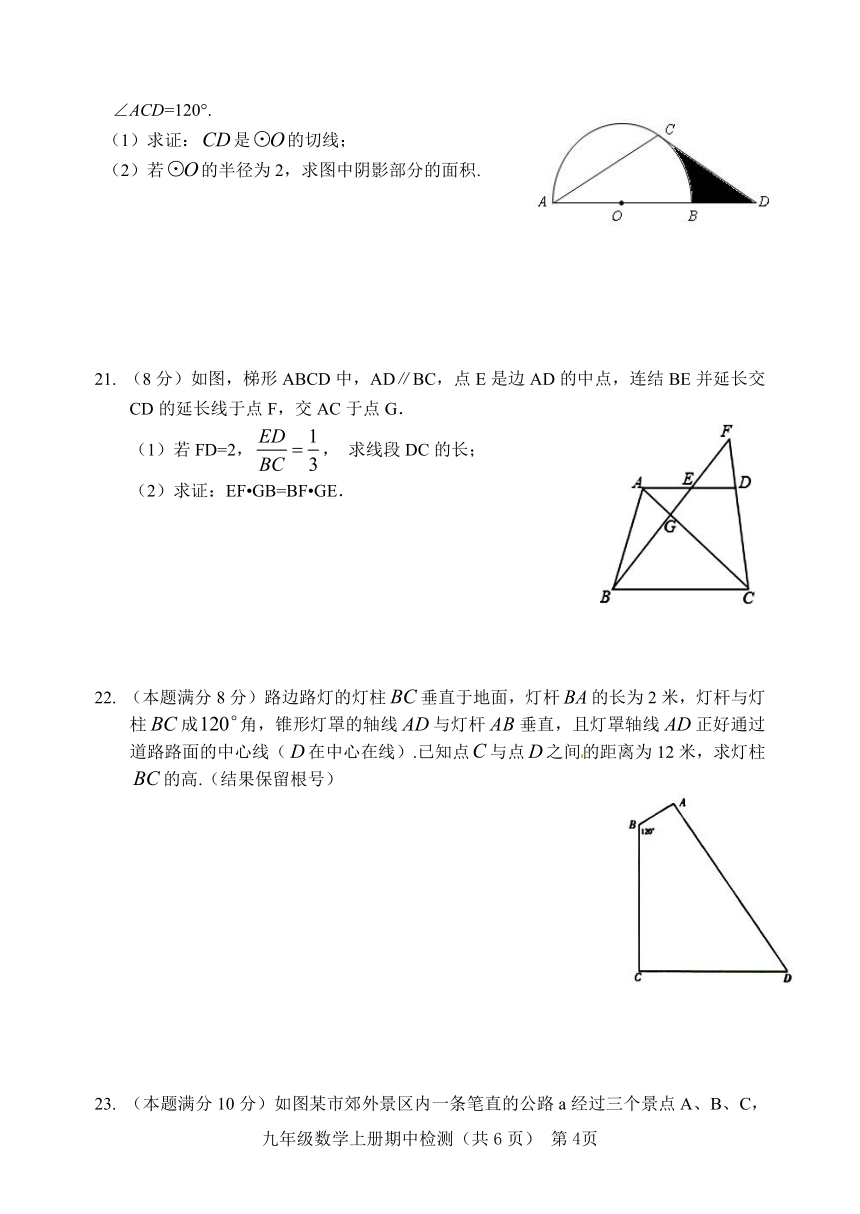
∠ACD=120°.
(1)求证:是的切线;
(2)若的半径为2,求图中阴影部分的面积.
21. (8分)如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2,, 求线段DC的长;
(2)求证:EF?GB=BF?GE.
?
22. (本题满分8分)路边路灯的灯柱垂直于地面,灯杆的长为2米,灯杆与灯柱成角,锥形灯罩的轴线与灯杆垂直,且灯罩轴线正好通过道路路面的中心线(在中心在线).已知点与点之间的距离为12米,求灯柱的高.(结果保留根号)
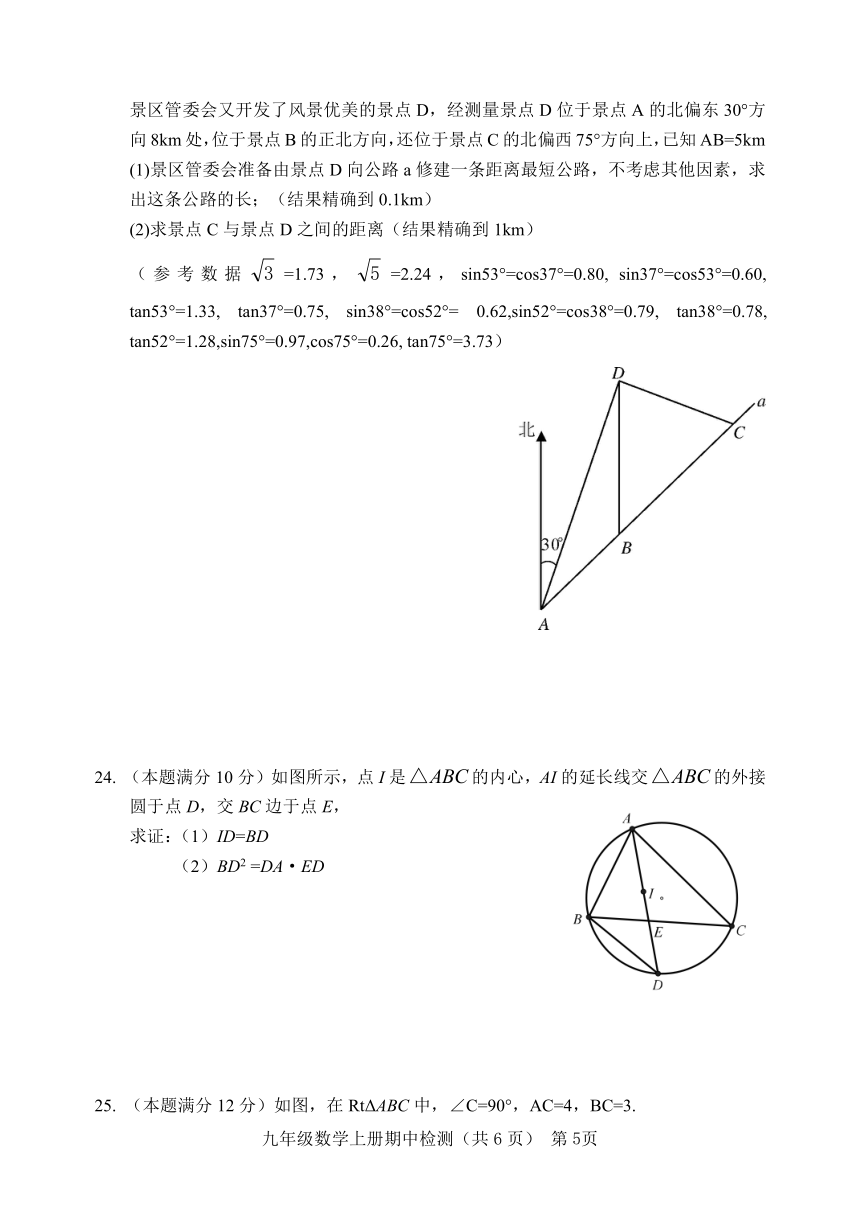
23. (本题满分10分)如图某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km
(1)景区管委会准备由景点D向公路a修建一条距离最短公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离(结果精确到1km)
(参考数据=1.73,=2.24,sin53°=cos37°=0.80, sin37°=cos53°=0.60, tan53°=1.33, tan37°=0.75, sin38°=cos52°= 0.62,sin52°=cos38°=0.79, tan38°=0.78, tan52°=1.28,sin75°=0.97,cos75°=0.26, tan75°=3.73)
24. (本题满分10分)如图所示,点I是的内心,AI的延长线交的外接圆于点D,交BC边于点E,
求证:(1)ID=BD
(2)BD2 =DA·ED
25. (本题满分12分)如图,在RtΔABC中,∠C=90°,AC=4,BC=3.
(1)如图(1),四边形DEFG为ABC的内接正方形,求正方形的边长.
(2)如图(2),三角形内有并排的两个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(3)如图(3),三角形内有并排的三个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(4) 如图(4),三角形内有并排的n个相等的正方形,它们组成的矩形内接于ΔABC,请写出正方形的边长
参 考 答 案
一、选择题(每小题3分,共36分)
1.B 2.B 3.C 4.B 5.A 6.B 7.D 8.C 9.C 10.A 11. D 12. C
二、填空题(每小题3分,共15分)
13. 4π 14. 5:3:12 15. (1,0)或(-1,0) 16. 17. (0,4+)
三、解答题:(共69分)
18. (6分)(1)1;(2)
19. (7分)π
20.(8分)(1)证明:连接OC.
∵AC=CD,
∴∠CAD=∠CDA.
∵∠ACD=120°,
∴∠CAD=∠CDA=30°.
∵OA=OC,
∴∠OAC=∠OCA=30°,
∴∠COD=60°,
∴∠OCD=90°,
∴CD是⊙O的切线.
(2)∵∠OCD=90°,OC=2,∠CDO=30°,
∴CD=2
∴S△OCD=1/2×OC×CD=2∵∠COD=60°,
∴S扇形COB=60/360×π×22=2π/3,
∴S阴影=S△OCD-S扇形COB=2-π
21. (8分)(1)解:∵AD∥BC,
∴△DEF∽△CBF,
∴,
∴FC=3FD=6,
∴DC=FC﹣FD=4;
(2)证明:∵AD∥BC,
∴△DEF∽△CBF,△AEG∽△CBG,
∴
∵点E是边AD的中点,
∴AE=DE,
∴,
∴EF?GB=BF?GE.
22、(本题满分8分)
解:设灯柱BC的长为h米,作AH⊥CD于点H,作BE⊥AH于点E.
∴四边形BCHE为矩形。
∵∠ABC=120°,
∴∠ABE=30°.
又∵∠BAD=∠BCD=90°,
∴∠ADC=60°.
在Rt△AEB中,
∴AE=ABsin30°=1,
BE=ABcos30°=∴CH=又∵CD=12,
∴DH=12?
在Rt△AHD中,
tan∠ADH=AHHD=h+1/12?=
解得,h=12?4.
∴灯柱BC的高为(12?4)米.?????
23、(本题满分10分)
解: (1)如图,过点D作DE⊥AC于点E,
过点A作AF⊥DB,交DB的延长线于点F,
在Rt△DAF中,∠ADF=30?,
∴AF=AD=×8=4,
∴DF= 4
在Rt△ABF中BF= 3,
∴BD=DF?BF=4-3,
sin∠ABF==,
在Rt△DBE中,sin∠DBE=DE/BD,
∵∠ABF=∠DBE,
∴sin∠DBE=,
∴DE=BD?sin∠DBE=4/5×(4?3)=(16?12)/5≈3.1(km),
∴景点D向公路a修建的这条公路的长约是3.1km;
由题意可知∠CDB=75?,
由(1)可知sin∠DBE=4/5=0.8,所以∠DBE=53?,
∴∠DCB=180??75??53?=52?,
在Rt△DCE中,sin∠DCE=DEDC,
∴DC=DE/sin52?≈3.1/0.79≈4(km),
∴景点C与景点D之间的距离约为4km.
24. (本题满分10分)
解:证明:(1)连结BI,BD
∵ I为△ABC的内心
∴ ∠BAD=∠DAC ∠CBI=∠IBA (三角形的内心与顶点的连线平分各角)
∵ ∠DBC、∠DAC是同弧所对的圆周角
∴ ∠DBC=∠DAC (同圆或等圆中,等弧所对的圆周角相等)
∵ ∠BAD=∠DAC ∠DBC=∠DAC
∴ ∠BAD=∠DBC
∵ ∠BID=∠IBA+∠BAD ∠DBI=∠DBC+∠CBI ∠CBI=∠IBA ∠BAD=∠DBC
∴ ∠BID=∠DBI
∴ ID=BD (等角对等边)
(2) ∵ ∠BAD=∠DBC ∠ADB=∠ADB
∴ △BDE∽△ADB (两角对应相等的两个三角形相似)
∴?BDED=ADBD?(相似三角形的三边对应成比例)
∴?BD2=AD×ED
∵?BD2=AD×ED,?ID=BD
∴?ID2=AD×ED
25、 (本题满分12分)
解:(1)在图1中作CN⊥AB,交GF于点M,交AB于点N.
在Rt△ABC中,∵AC=4,BC=3,∴AB=5,CN=,
∵GF∥AB,∴△CGF∽△CAB,∴=,
设正方形边长为x,则(?x) ÷()=, ∴x=;
(2) 在图2中作CN⊥AB,交GF于点M,交AB于点N.
∵GF∥AB,∴△CGF∽△CAB,∴=,
设每个正方形边长为x,则(?x) ÷()=∴x=
(3)在图3中,作CN⊥AB,交GF于点M,交AB于点N,
∵GF∥AB,∴△CGF∽△CAB,∴=,
设每个正方形的边长为x,则(?x) ÷()=,∴x=
(4)设每个正方形的边长为x,同理得到:(?x) ÷()=,
则x=.
第7题
E
H
F
G
C
B
A
O
A
y
B
PAGE
九年级数学上册期中检测(共6页) 第5页
九年级数学
(时间100分钟,满分120分)
一、选择题(每小题3分,共36分)
1. 下列说法①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81,正确的有( )
A.1个 B.2个 C.3个 D.4个
2. 下列计算正确的是( )
A. B.
C. D.
3. 等腰直角三角形的外接圆半径等于( )
A.腰长 B.腰长的; C.底边的 D.腰上的高
4.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.ABM∽ACB B.ANC∽AMB C.ANC∽ACM D.CMN∽BCA
5.如图,沿折叠矩形纸片,使点落在边的点处.已知,,则的值为 ( )
A. B. C. D.
6.在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
A. B. C. D.
第4题 第5题 第6题
7.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )。
A.πr2 B.πr2
C.πr2 D.πr2
8.一人乘雪橇沿坡比1∶的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s =10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为( )
A.72 m B.36 m C.36 m D.18 m
9.⊙O的弦AB等于半径,那么弦AB所对的圆周角一定是( ).
A.30° B.150° C.30°或150° D.60°或120°
10.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大3.5米 B.减小1.5米
C.增大1.5米 D.减小3.5米
11.如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE=8,设∠ACE=α,则tanα的值为( )
A. B.
C.2 D.
12.如图,ΔADE绕正方形ABCD的顶点A顺时针旋转90°,得ΔABF,连结EF交AB于H,则下列结论错误的是( )
A.AE⊥AF B.EF∶AF=∶1
C.AF2=FH?FE D.FB∶FC=HB∶EC
二、填空题(每小题3分,共15分)
13. 已知,Rt△ABC中,∠C=90°,AC=6,AB=10,则三角形内切圆的面积为____________.
14. 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PQ:QC= .
15. 如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为 ??时, 使得△BOC∽△AOB.
16. 如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的
15题图 16题图 17题图
17. 如图,机器人从A点,沿着西南方向,行了个4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为 (结果保留根号).
三、解答题
18. 计算:(6分)
(1)
(2) HYPERLINK "http://www.mathschina.com/Index.html"
19.(7分)如图,阴影部分是由同心圆的与所围成的. 已知OA=3cm,OC=2cm,∠AOB=120o,求阴影部分的面积(结果保留π).
20.(8分)如图,点在的直径的延长线上,点在上,且,
∠ACD=120°.
(1)求证:是的切线;
(2)若的半径为2,求图中阴影部分的面积.
21. (8分)如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2,, 求线段DC的长;
(2)求证:EF?GB=BF?GE.
?
22. (本题满分8分)路边路灯的灯柱垂直于地面,灯杆的长为2米,灯杆与灯柱成角,锥形灯罩的轴线与灯杆垂直,且灯罩轴线正好通过道路路面的中心线(在中心在线).已知点与点之间的距离为12米,求灯柱的高.(结果保留根号)
23. (本题满分10分)如图某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km
(1)景区管委会准备由景点D向公路a修建一条距离最短公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离(结果精确到1km)
(参考数据=1.73,=2.24,sin53°=cos37°=0.80, sin37°=cos53°=0.60, tan53°=1.33, tan37°=0.75, sin38°=cos52°= 0.62,sin52°=cos38°=0.79, tan38°=0.78, tan52°=1.28,sin75°=0.97,cos75°=0.26, tan75°=3.73)
24. (本题满分10分)如图所示,点I是的内心,AI的延长线交的外接圆于点D,交BC边于点E,
求证:(1)ID=BD
(2)BD2 =DA·ED
25. (本题满分12分)如图,在RtΔABC中,∠C=90°,AC=4,BC=3.
(1)如图(1),四边形DEFG为ABC的内接正方形,求正方形的边长.
(2)如图(2),三角形内有并排的两个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(3)如图(3),三角形内有并排的三个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(4) 如图(4),三角形内有并排的n个相等的正方形,它们组成的矩形内接于ΔABC,请写出正方形的边长
参 考 答 案
一、选择题(每小题3分,共36分)
1.B 2.B 3.C 4.B 5.A 6.B 7.D 8.C 9.C 10.A 11. D 12. C
二、填空题(每小题3分,共15分)
13. 4π 14. 5:3:12 15. (1,0)或(-1,0) 16. 17. (0,4+)
三、解答题:(共69分)
18. (6分)(1)1;(2)
19. (7分)π
20.(8分)(1)证明:连接OC.
∵AC=CD,
∴∠CAD=∠CDA.
∵∠ACD=120°,
∴∠CAD=∠CDA=30°.
∵OA=OC,
∴∠OAC=∠OCA=30°,
∴∠COD=60°,
∴∠OCD=90°,
∴CD是⊙O的切线.
(2)∵∠OCD=90°,OC=2,∠CDO=30°,
∴CD=2
∴S△OCD=1/2×OC×CD=2∵∠COD=60°,
∴S扇形COB=60/360×π×22=2π/3,
∴S阴影=S△OCD-S扇形COB=2-π
21. (8分)(1)解:∵AD∥BC,
∴△DEF∽△CBF,
∴,
∴FC=3FD=6,
∴DC=FC﹣FD=4;
(2)证明:∵AD∥BC,
∴△DEF∽△CBF,△AEG∽△CBG,
∴
∵点E是边AD的中点,
∴AE=DE,
∴,
∴EF?GB=BF?GE.
22、(本题满分8分)
解:设灯柱BC的长为h米,作AH⊥CD于点H,作BE⊥AH于点E.
∴四边形BCHE为矩形。
∵∠ABC=120°,
∴∠ABE=30°.
又∵∠BAD=∠BCD=90°,
∴∠ADC=60°.
在Rt△AEB中,
∴AE=ABsin30°=1,
BE=ABcos30°=∴CH=又∵CD=12,
∴DH=12?
在Rt△AHD中,
tan∠ADH=AHHD=h+1/12?=
解得,h=12?4.
∴灯柱BC的高为(12?4)米.?????
23、(本题满分10分)
解: (1)如图,过点D作DE⊥AC于点E,
过点A作AF⊥DB,交DB的延长线于点F,
在Rt△DAF中,∠ADF=30?,
∴AF=AD=×8=4,
∴DF= 4
在Rt△ABF中BF= 3,
∴BD=DF?BF=4-3,
sin∠ABF==,
在Rt△DBE中,sin∠DBE=DE/BD,
∵∠ABF=∠DBE,
∴sin∠DBE=,
∴DE=BD?sin∠DBE=4/5×(4?3)=(16?12)/5≈3.1(km),
∴景点D向公路a修建的这条公路的长约是3.1km;
由题意可知∠CDB=75?,
由(1)可知sin∠DBE=4/5=0.8,所以∠DBE=53?,
∴∠DCB=180??75??53?=52?,
在Rt△DCE中,sin∠DCE=DEDC,
∴DC=DE/sin52?≈3.1/0.79≈4(km),
∴景点C与景点D之间的距离约为4km.
24. (本题满分10分)
解:证明:(1)连结BI,BD
∵ I为△ABC的内心
∴ ∠BAD=∠DAC ∠CBI=∠IBA (三角形的内心与顶点的连线平分各角)
∵ ∠DBC、∠DAC是同弧所对的圆周角
∴ ∠DBC=∠DAC (同圆或等圆中,等弧所对的圆周角相等)
∵ ∠BAD=∠DAC ∠DBC=∠DAC
∴ ∠BAD=∠DBC
∵ ∠BID=∠IBA+∠BAD ∠DBI=∠DBC+∠CBI ∠CBI=∠IBA ∠BAD=∠DBC
∴ ∠BID=∠DBI
∴ ID=BD (等角对等边)
(2) ∵ ∠BAD=∠DBC ∠ADB=∠ADB
∴ △BDE∽△ADB (两角对应相等的两个三角形相似)
∴?BDED=ADBD?(相似三角形的三边对应成比例)
∴?BD2=AD×ED
∵?BD2=AD×ED,?ID=BD
∴?ID2=AD×ED
25、 (本题满分12分)
解:(1)在图1中作CN⊥AB,交GF于点M,交AB于点N.
在Rt△ABC中,∵AC=4,BC=3,∴AB=5,CN=,
∵GF∥AB,∴△CGF∽△CAB,∴=,
设正方形边长为x,则(?x) ÷()=, ∴x=;
(2) 在图2中作CN⊥AB,交GF于点M,交AB于点N.
∵GF∥AB,∴△CGF∽△CAB,∴=,
设每个正方形边长为x,则(?x) ÷()=∴x=
(3)在图3中,作CN⊥AB,交GF于点M,交AB于点N,
∵GF∥AB,∴△CGF∽△CAB,∴=,
设每个正方形的边长为x,则(?x) ÷()=,∴x=
(4)设每个正方形的边长为x,同理得到:(?x) ÷()=,
则x=.
第7题
E
H
F
G
C
B
A
O
A
y
B
PAGE
九年级数学上册期中检测(共6页) 第5页
同课章节目录
