2019-2020学年沪教新版小学六年级上册期中考试数学试卷8(解析版)
文档属性
| 名称 | 2019-2020学年沪教新版小学六年级上册期中考试数学试卷8(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 18:50:14 | ||
图片预览




文档简介
2019-2020学年沪教新版小学六年级期中考试数学试卷
一.选择题(共10小题)
1.不与56相邻的数是( )
A.55 B.58 C.57
2.93000000中的“9”表示9个( )
A.千万 B.百万 C.亿
3.一个数既是48的因数,又是6的倍数,这个数不可能是( )
A.48 B.24 C.16 D.12
4.有两个不同的质数的和是14,它们的积是( )
A.33 B.24 C.13 D.45
5.甲数的等于乙数的,那么( )
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数 D.无法比较
6.a、b、c都是大于1的自然数.根据a×=×b=c÷的等式判断,最大的是( )
A.a B.b C.c D.一样大
7.下列算式中,结果最大的是( )
A. + B.×59 C.÷
8.下面的分数能化成有限小数的是( )
A. B. C. D.
9.下列语句正确的有( )个.
(1)1吨的和4吨的一样重.
(2)一根电线长3米,用去米后,还剩下米.
(3)60的相当于80的.
A.1 B.2 C.3 D.0
10.公园里,松树占树木总数的,柳树占总数的,两种树共占总数的几分之几?其他树木占总数的几分之几?正确的是( )
A.两种树共占总数的,其他树木占总数的
B.两种树共占总数的,其他树木占总数的
C.两种树共占总数的,其他树木占总数的
D.两种树共占总数的,其他树木占总数的
二.填空题(共10小题)
11.5□中最大填 时这个数能被3整除,这个数的因数有 .
12.二十三亿九千七百万是由2个 ,3个 ,9个 和7个 组成的.
13.24的所有因数: ,50以内7的所有倍数: .
14.在一位数中,最小的质数与最大的偶数相乘,积是 .
15.60吨比 吨少,比36kg多是 kg.
16.把0.8、、83%、按从大到小的顺序排列 .
17.
= = = 2=
1﹣35%= = = 1=
18.=
19.一本故事书有340页,第一周看了全书的,第二周看的是第一周的,第二周看了 页.
20.一根绳子长米,比另一根长米,两根绳子共长 米.
三.判断题(共5小题)
21.个位是上3、6、9的数是一定是3的倍数. (判断对错)
22.同时是2、3、5、6的倍数中,最小的数是60. (判断对错)
23.假分数一定大于真分数. (判断对错)
24.1﹣,就是4个减去1个,剩下3个,等于. (判断对错)
25.全班人数的的就是全班人数的. (判断对错)
四.计算题(共2小题)
26.一个质数的2倍与另一个质数的3倍的和是100,这两个质数分别是多少?
27.口算
÷=
1﹣=
3×=
6×=
五.操作题(共1小题)
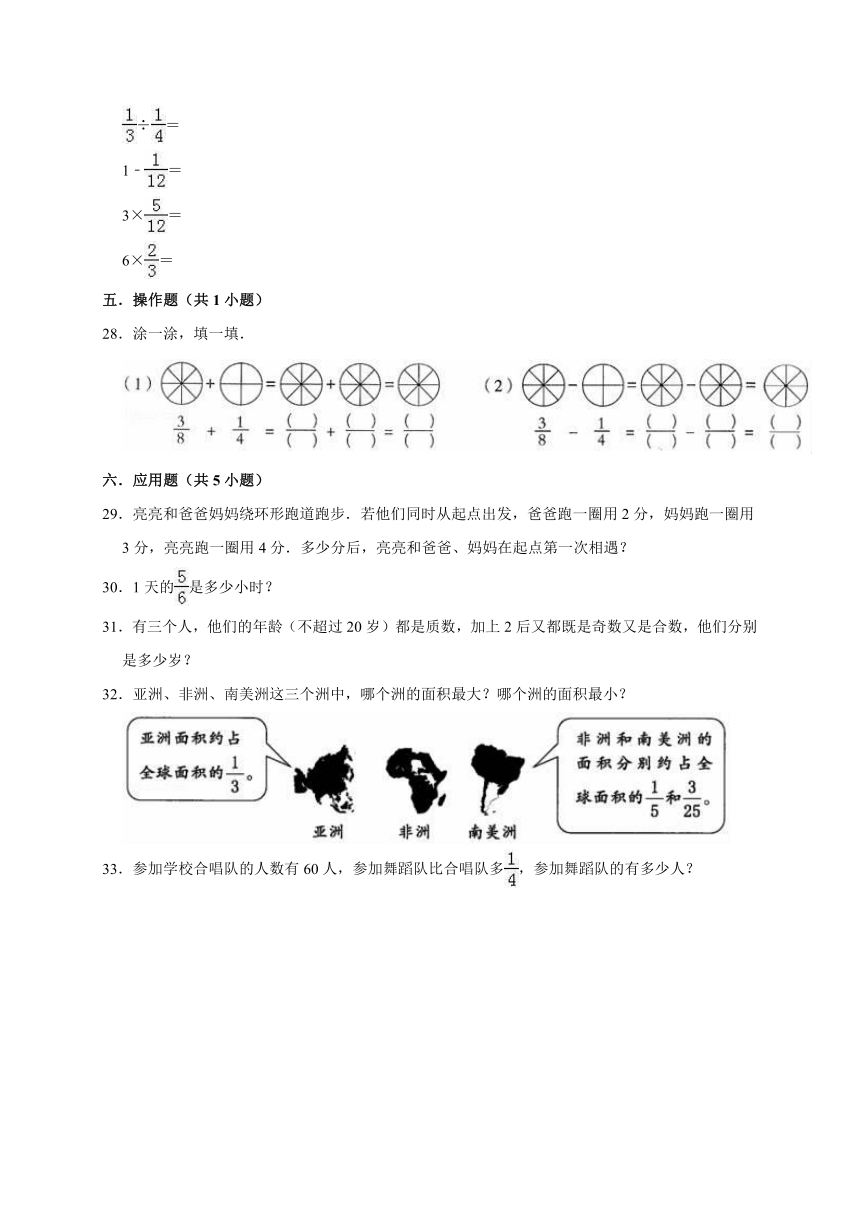
28.涂一涂,填一填.
六.应用题(共5小题)
29.亮亮和爸爸妈妈绕环形跑道跑步.若他们同时从起点出发,爸爸跑一圈用2分,妈妈跑一圈用3分,亮亮跑一圈用4分.多少分后,亮亮和爸爸、妈妈在起点第一次相遇?
30.1天的是多少小时?
31.有三个人,他们的年龄(不超过20岁)都是质数,加上2后又都既是奇数又是合数,他们分别是多少岁?
32.亚洲、非洲、南美洲这三个洲中,哪个洲的面积最大?哪个洲的面积最小?
33.参加学校合唱队的人数有60人,参加舞蹈队比合唱队多,参加舞蹈队的有多少人?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】与一个数相邻的数,是指这个数前面的一个数和后面的一个数;要求与56相邻的数,就是求56前面的一个数和后面的一个数,56前面的数是56﹣1=55,后面的数是56+1=57.
【解答】解:在55,58,57三个数中,不与56相邻的数是58;
故选:B.
【点评】求与一个数相邻的数,就是用这个数减去1或加上1.
2.【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位.
【解答】解:93000000中的“9”在千万位上表示9个千万;
故选:A.
【点评】此题考查整数中的数字所表示的意义,解答时一定要看清数位和这个数位的计数单位.
3.【分析】根据求一个数倍数的方法,先找出48的所有因数,再找出6的几个倍数;然后根据求一个数因数的方法,进而确定符合题意的数得解.
【解答】解:48的因数有:1、2、3、4、6、8、12、16、24、48;
48以内6的倍数有:6、12、18、24、30、36、42、48.
所以一个数既是48的因数,又是6的倍数,这个数是:12、24、48,不可能是16.
答:这个数不可能是16.
故选:C.
【点评】解决此题关键是掌握求一个数倍数的方法,以及求一个数因数的方法;要明确一个数倍数的个数是无限的,而一个数因数的个数是有限的.
4.【分析】根据质数的意义,一个数如果只有1和它的本身两个因数,这样的数叫做质数.两个不同的质数的和是14,那么这两个质数是11和3,再求出它们的积即可.
【解答】解:两个不同的质数的和是14,那么这两个质数是3和11,
3×11=33,
故选:A.
【点评】此题考查了质数的意义,掌握100以内的质数表是解答此题的关键.
5.【分析】由题意可知:甲数×=乙数×,于是可以分两种情况解答:(1)当甲乙两数不相等时,逆运用比例的基本性质,得出两数的比,问题即可得解;(2)当甲乙两数等于0时,等式仍然成立,据此即可得解.
【解答】解:由题意可得,甲数×=乙数×,
(1)甲数:乙数=:=3:4,所以甲数<乙数;
(2)当甲乙两数等于0时,等式仍然成立,所以甲数等于乙数.
故选:D.
【点评】此类题目,若没规定两数的取值范围,要分两种情进行解答.
6.【分析】a×=×b=c÷中先把c÷化成乘法,它们的积相等,只要比较已知的因数,已知的因数越大,另一个因数就越小,由此求解.
【解答】解:c÷=c×
a×=×b=c×
因为>>
所以:a>c>b,最大的是a.
故选:A.
【点评】解决本题先把除法化成乘法,再根据积一定,一个因数越大,另一个因数越小进行比较.
7.【分析】根据小数加法和乘除法的计算方法,分别求出各自的结果,然后再根据小数大小比较的方法进行解答.
【解答】解:因为+=
×59=
÷=1
>>1
所以结果最大的是×59.
故选:B.
【点评】关键是求出它们的结果,然后再进一步解答.
8.【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先约分,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数;如果分母中含有2或5以外的质因数,这个分数就不能化成有限小数,据此解答即可.
【解答】解:、的分母中含有质因数3,=的分母中含有质因数3,都不能化成有限小数;
化简后是,分母中只含有质因数5,能化成有限小数;
故选:D.
【点评】此题主要考查什么样的分数可以化成有限小数,一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数.
9.【分析】(1)1吨的是1×=(吨);4吨的为4×=(吨),再比较大小即可.
(2)用去米,运用减法即可求出身下的量为:3=2.6(米),再比较大小即可.
(3)60的是60×=24(吨);80的是80×=24(吨);再比较大小即可.
【解答】解:(1)1×=(吨);4×=(吨);故本题正确.
(2)3=2.6(米),2.6;故本题错误.
(3)60×=24(吨);80×=24(吨);故本题正确.
故选:B.
【点评】找清单位“1”,利用基本数量关系解决问题;注意带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几.
10.【分析】把树木的总数看成单位“1”,松树占树木总数的,柳树占总数的,把这两个分率相加,即可求出两种树共占总数的几分之几,再用1减去这两种树木占分率,即可求出其他树木占总数的几分之几.
【解答】解: +=
1﹣=
答:两种树共占总数的,其他树木占总数的.
故选:A.
【点评】解决本题关键是理解把总数看成单位“1”,再根据加减法的意义求解.
二.填空题(共10小题)
11.【分析】首先根据是3的倍数的数各个位上的数相加所得的和能被3整除,判断出5□中最大填多少时这个数能被3整除;然后根据找一个数的因数,可以一对一对的找,把求出的数写成两个数的乘积,那么每一个乘积中的因数都是它的因数,然后从小到大依次写出即可.
【解答】解:5□中最大填7时这个数能被3整除,
因为57=1×57=3×19,
所以57的因数有:1、3、19、57.
故答案为:7;1、3、19、57.
【点评】此题主要考查了是3的倍数的数的特征,以及找一个数的因数的方法,要熟练掌握.
12.【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位;据此解答.
【解答】解:二十三亿九千七百万是由2个十亿,3个亿,9个千万和7个百万组成的;
故答案为:十亿,亿,千万,百万.
【点评】此题考查整数中的数字所表示的意义:有几个计数单位;解答时一定要看清数位和这个数位的计数单位.
13.【分析】求一个数的因数,就是用这个数除以小于等于这个数的自然数(0除外),能够除尽的自然数就是这个数的因数;求一个数的倍数,就是让这个数乘自然数1、2、3……得出来的积就是这个数的倍数.
【解答】解:24的所有因数有:1、2、3、4、6、8、12、24;50以内7的所有倍数:7、14、21、28、35、42、49.
故答案为:1、2、3、4、6、8、12、24;7、14、21、28、35、42、49.
【点评】此题考查了因数的特点及求法,倍数的特点及求法,注意平时基础知识的积累.
14.【分析】根据质数、偶数的意义,一个数如果只有1和它本身两个因数,这样的数叫做质数,在自然数中,是2的倍数的数叫做偶数.在一位数中,最小的质数是2,最大的偶数8,据此解答.
【解答】解:在一位数中,最小的质数是2,最大的偶数8,2×8=16,
故答案为:16.
【点评】此题考查的目的是理解质数、偶数的意义.
15.【分析】首先根据题意,把所求的重量看作单位“1”,则60吨占所求的重量的(1﹣=);再根据分数除法的意义,用60除以它占所求的重量的分率即可;
然后根据题意,把36kg看作单位“1”,然后根据分数乘法的意义,用36乘所求的重量占36kg的分率即可.
【解答】解:60÷(1﹣)
=60÷
=80(吨)
所以60吨比80吨少;
36×(1+)
=36×
=48(kg)
所以比36kg多是48kg.
故答案为:80、48.
【点评】此题主要考查了分数乘法、分数除法的运算方法,要熟练掌握,注意弄清楚题中的各个量之间的数量关系.
16.【分析】先把、83%、都化成小数,再根据小数比较大小的方法进行比较.
【解答】解:≈0.8333、
83%=0.83、
≈0.875
0.875>0.833>0.83>0.8
即:>>83%>0.8.
故答案为:>>83%>0.8.
【点评】比较不同形式数的大小,一般先都化成小数,再根据小数比较大小的方法求解.
17.【分析】①②通分计算;③约分计算;④⑥⑧把除法改为乘法,再计算;⑤⑦把百分数化为分数计算.
【解答】解:
= = = 2=7
1﹣35%= = = 1=1000
【点评】此题考查了在计算中运用通分、约分、数字转化等知识进行计算的能力.
18.【分析】100个的和相加,属于求几个相同加数和的运算,用乘法计算即可.
【解答】解:
=×100
=37.5
故答案为:37.5.
【点评】此题考查了分数乘整数的意义:求几个相同加数和的简便运算.
19.【分析】首先根据题意,把全书的页数看作单位“1”,根据分数乘法的意义,用全书的页数乘第一周看的占的分率,求出第一周看了多少页;然后根据题意,把第一周看的页数看作单位“1”,根据分数乘法的意义,用第一周的页数乘第二周看的占第一周的分率,求出第二周看了多少页即可.
【解答】解:340××
=85×
=136(页)
答:第二周看了136页.
故答案为:136.
【点评】此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是要明确:求一个数的几分之几是多少,用乘法解答.
20.【分析】先用第一根绳子的长度减去米,求出另一根的长度,再把两根的长度相加即可求解.
【解答】解:﹣+
=++
=﹣
=(米)
答:两根绳子共长米.
故答案为:.
【点评】解决本题根据加减法的意义进行求解即可.
三.判断题(共5小题)
21.【分析】举个反例证明.3的倍数的特征:各个数位上的数的和是3的倍数,这个数就是3的倍数.
【解答】解:13、16、29是个位上分别是3、6、9,可是它们都不是3的倍数,
所以个位上是3、6、9的数,一定是3的倍数的说法是错误的.
故答案为:×.
【点评】本题主要考查3的倍数的特征.注意个位上是3、6、9的数不一定是3的倍数,各个数位上的数的和是3的倍数,这个数就是3的倍数.
22.【分析】本题即求2、3、5、6的最小公倍数,因为2、3的最小公倍数是6,所以只要求出5、6的最小公倍数即可判断.
【解答】解:因为2、3的最小公倍数是6,所以只要求出5、6的最小公倍数,
5×6=30
即同时是2、3、5、6倍数的最小的数是30,所以本题说法错误;
故答案为:×.
【点评】此题实际上就是求2、3、5、6的最小公倍数.
23.【分析】分子大于或等于分母的分数是假分数,假分数大于或等于1,分子小于分母的分数是真分数,真分数小于1.据此解答.
【解答】解:因假分数大于或等于1,真分数小于1,扬眉假分数一定大于真分数.
故答案为:√.
【点评】本题主要考查了学生对真分数和假分数意义的掌握情况.
24.【分析】1﹣,把1变为4个,再减去1个,即可得到剩下3个,从而求解.
【解答】解:1﹣,就是4个减去1个,剩下3个,等于.
故答案为:√.
【点评】考查了分数的减法运算,关键是把1变为4个再相减.
25.【分析】先把全班的总人数看成单位“1”,它的的就是×=,由此进行判断即可.
【解答】解:×=
全班人数的的就是全班人数的
所以原题说法正确;
故答案为:√.
【点评】本题考查了一个数乘分数的意义:求这个数的几分之几是多少.
四.计算题(共2小题)
26.【分析】质数有2、3、5、7、11、13、17…,设其中一个质数为x,另一个质数为y,根据等量关系:一个质数的3倍与另一个质数的2倍之和等于100即可列出一个二元一次方程,求得符合题意的整数解即可解决问题.
【解答】解:设其中一个质数为x,另一个质数为y,根据题意可得方程:
3x+2y=100
y=
根据上式特点可知,要使y有整数解,x必须是偶数,
因为所有的质数中,只有2是偶数,所以这个方程的整数解只有一组:
当x=2时,y=47;
答:这两个质数是2和47.
【点评】此题要考查了质数的性质的灵活应用,特别是解这个二元一次方程时,紧扣能被2整除的数的特征和质数的特点,是解这个不定方程的关键.此题要考查了质数的性质的灵活应用,特别是解这个二元一次方程时,紧扣能被2整除的数的特征和质数的特点,是解这个不定方程的关键.
27.【分析】根据分数减法和乘除法的计算方法直接口算即可.
【解答】解:÷=
1﹣=
3×=
6×=4
【点评】此题考查了学生的口算能力,属于基础题,细心计算即可解答.
五.操作题(共1小题)
28.【分析】根据异分母的分数加减法的计算方法,表示把一个圆平均分成8份,表示3份,表示把一个圆平均分成4份,表示1份;先涂色表示分数,再通分,然后再根据同分母分数加减法的计算方法进行计算.
【解答】解:
【点评】异分母相加减,先通分,化成同分母后,再按同分母分数加减法进行计算.
六.应用题(共5小题)
29.【分析】此题实际上就是求2,3,4的最小公倍数,这个最小公倍数就是他们在起点第一次相遇的时间;据此解答即可.
【解答】解:因为4是2的倍数,4和3互质,
所以,3×4=12(分钟)
答:12分后,亮亮和爸爸、妈妈在起点第一次相遇.
【点评】本题考查了公倍数应用题,考查了学生运用求最小公倍数的方法解决行程问题的能力.
30.【分析】首先根据题意,把1天(24小时)看作单位“1”,然后根据分数乘法的意义,用24乘,求出1天的是多少小时即可.
【解答】解:1天=24小时
24×=20(小时)
答:1天的是20小时.
【点评】此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是要明确:求一个数的几分之几是多少,用乘法解答.
31.【分析】根据奇数与偶数、质数与合数的意义,是2的倍数的数叫做偶数.不是2的倍数的数叫做奇数,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.一个自然数,如果除了1和它本身还有别的因数,这样的数叫做合数.先找出20以内的质数,然后把它们分别加上2,然后看得数既是奇数又是合数的,由此解答.
【解答】解:质数有:2,3,5,7,11,13,17,19;
加上2后:
2+2=4
3+2=5
5+2=7
7+2=9
11+2=13
13+2=15
17+2=19
19+2=21
因为加上2后既是奇数又是合数9,15,21;
所以符合要求的质数是:7,13,19;
答:这三个人分别是7岁、13岁、19岁.
【点评】此题考查的目的是使学生理解和掌握奇数与偶数、质数与合数的概念及意义.
32.【分析】依据分数基本性质,把三个洲占陆地面积通分为分母为75的分数,再依据同分母分数大小比较方法即可解答.
【解答】解:==
因为:>>
所以:>>.
答:亚洲的陆地面积最大,南美洲的陆地面积最少.
【点评】本题考查知识点:依据分数基本性质正确解决问题.
33.【分析】把合唱队的人数看成单位“1”,舞蹈队的人数比合唱队多,那么舞蹈队的人数就是合唱队的(1+),用合唱队的人数乘上这个分率,就是舞蹈队的人数.
【解答】解:60×(1+)
=60×
=75(人)
答:参加舞蹈队的有75人.
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法计算.
一.选择题(共10小题)
1.不与56相邻的数是( )
A.55 B.58 C.57
2.93000000中的“9”表示9个( )
A.千万 B.百万 C.亿
3.一个数既是48的因数,又是6的倍数,这个数不可能是( )
A.48 B.24 C.16 D.12
4.有两个不同的质数的和是14,它们的积是( )
A.33 B.24 C.13 D.45
5.甲数的等于乙数的,那么( )
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数 D.无法比较
6.a、b、c都是大于1的自然数.根据a×=×b=c÷的等式判断,最大的是( )
A.a B.b C.c D.一样大
7.下列算式中,结果最大的是( )
A. + B.×59 C.÷
8.下面的分数能化成有限小数的是( )
A. B. C. D.
9.下列语句正确的有( )个.
(1)1吨的和4吨的一样重.
(2)一根电线长3米,用去米后,还剩下米.
(3)60的相当于80的.
A.1 B.2 C.3 D.0
10.公园里,松树占树木总数的,柳树占总数的,两种树共占总数的几分之几?其他树木占总数的几分之几?正确的是( )
A.两种树共占总数的,其他树木占总数的
B.两种树共占总数的,其他树木占总数的
C.两种树共占总数的,其他树木占总数的
D.两种树共占总数的,其他树木占总数的
二.填空题(共10小题)
11.5□中最大填 时这个数能被3整除,这个数的因数有 .
12.二十三亿九千七百万是由2个 ,3个 ,9个 和7个 组成的.
13.24的所有因数: ,50以内7的所有倍数: .
14.在一位数中,最小的质数与最大的偶数相乘,积是 .
15.60吨比 吨少,比36kg多是 kg.
16.把0.8、、83%、按从大到小的顺序排列 .
17.
= = = 2=
1﹣35%= = = 1=
18.=
19.一本故事书有340页,第一周看了全书的,第二周看的是第一周的,第二周看了 页.
20.一根绳子长米,比另一根长米,两根绳子共长 米.
三.判断题(共5小题)
21.个位是上3、6、9的数是一定是3的倍数. (判断对错)
22.同时是2、3、5、6的倍数中,最小的数是60. (判断对错)
23.假分数一定大于真分数. (判断对错)
24.1﹣,就是4个减去1个,剩下3个,等于. (判断对错)
25.全班人数的的就是全班人数的. (判断对错)
四.计算题(共2小题)
26.一个质数的2倍与另一个质数的3倍的和是100,这两个质数分别是多少?
27.口算
÷=
1﹣=
3×=
6×=
五.操作题(共1小题)
28.涂一涂,填一填.
六.应用题(共5小题)
29.亮亮和爸爸妈妈绕环形跑道跑步.若他们同时从起点出发,爸爸跑一圈用2分,妈妈跑一圈用3分,亮亮跑一圈用4分.多少分后,亮亮和爸爸、妈妈在起点第一次相遇?
30.1天的是多少小时?
31.有三个人,他们的年龄(不超过20岁)都是质数,加上2后又都既是奇数又是合数,他们分别是多少岁?
32.亚洲、非洲、南美洲这三个洲中,哪个洲的面积最大?哪个洲的面积最小?
33.参加学校合唱队的人数有60人,参加舞蹈队比合唱队多,参加舞蹈队的有多少人?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】与一个数相邻的数,是指这个数前面的一个数和后面的一个数;要求与56相邻的数,就是求56前面的一个数和后面的一个数,56前面的数是56﹣1=55,后面的数是56+1=57.
【解答】解:在55,58,57三个数中,不与56相邻的数是58;
故选:B.
【点评】求与一个数相邻的数,就是用这个数减去1或加上1.
2.【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位.
【解答】解:93000000中的“9”在千万位上表示9个千万;
故选:A.
【点评】此题考查整数中的数字所表示的意义,解答时一定要看清数位和这个数位的计数单位.
3.【分析】根据求一个数倍数的方法,先找出48的所有因数,再找出6的几个倍数;然后根据求一个数因数的方法,进而确定符合题意的数得解.
【解答】解:48的因数有:1、2、3、4、6、8、12、16、24、48;
48以内6的倍数有:6、12、18、24、30、36、42、48.
所以一个数既是48的因数,又是6的倍数,这个数是:12、24、48,不可能是16.
答:这个数不可能是16.
故选:C.
【点评】解决此题关键是掌握求一个数倍数的方法,以及求一个数因数的方法;要明确一个数倍数的个数是无限的,而一个数因数的个数是有限的.
4.【分析】根据质数的意义,一个数如果只有1和它的本身两个因数,这样的数叫做质数.两个不同的质数的和是14,那么这两个质数是11和3,再求出它们的积即可.
【解答】解:两个不同的质数的和是14,那么这两个质数是3和11,
3×11=33,
故选:A.
【点评】此题考查了质数的意义,掌握100以内的质数表是解答此题的关键.
5.【分析】由题意可知:甲数×=乙数×,于是可以分两种情况解答:(1)当甲乙两数不相等时,逆运用比例的基本性质,得出两数的比,问题即可得解;(2)当甲乙两数等于0时,等式仍然成立,据此即可得解.
【解答】解:由题意可得,甲数×=乙数×,
(1)甲数:乙数=:=3:4,所以甲数<乙数;
(2)当甲乙两数等于0时,等式仍然成立,所以甲数等于乙数.
故选:D.
【点评】此类题目,若没规定两数的取值范围,要分两种情进行解答.
6.【分析】a×=×b=c÷中先把c÷化成乘法,它们的积相等,只要比较已知的因数,已知的因数越大,另一个因数就越小,由此求解.
【解答】解:c÷=c×
a×=×b=c×
因为>>
所以:a>c>b,最大的是a.
故选:A.
【点评】解决本题先把除法化成乘法,再根据积一定,一个因数越大,另一个因数越小进行比较.
7.【分析】根据小数加法和乘除法的计算方法,分别求出各自的结果,然后再根据小数大小比较的方法进行解答.
【解答】解:因为+=
×59=
÷=1
>>1
所以结果最大的是×59.
故选:B.
【点评】关键是求出它们的结果,然后再进一步解答.
8.【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先约分,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数;如果分母中含有2或5以外的质因数,这个分数就不能化成有限小数,据此解答即可.
【解答】解:、的分母中含有质因数3,=的分母中含有质因数3,都不能化成有限小数;
化简后是,分母中只含有质因数5,能化成有限小数;
故选:D.
【点评】此题主要考查什么样的分数可以化成有限小数,一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数.
9.【分析】(1)1吨的是1×=(吨);4吨的为4×=(吨),再比较大小即可.
(2)用去米,运用减法即可求出身下的量为:3=2.6(米),再比较大小即可.
(3)60的是60×=24(吨);80的是80×=24(吨);再比较大小即可.
【解答】解:(1)1×=(吨);4×=(吨);故本题正确.
(2)3=2.6(米),2.6;故本题错误.
(3)60×=24(吨);80×=24(吨);故本题正确.
故选:B.
【点评】找清单位“1”,利用基本数量关系解决问题;注意带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几.
10.【分析】把树木的总数看成单位“1”,松树占树木总数的,柳树占总数的,把这两个分率相加,即可求出两种树共占总数的几分之几,再用1减去这两种树木占分率,即可求出其他树木占总数的几分之几.
【解答】解: +=
1﹣=
答:两种树共占总数的,其他树木占总数的.
故选:A.
【点评】解决本题关键是理解把总数看成单位“1”,再根据加减法的意义求解.
二.填空题(共10小题)
11.【分析】首先根据是3的倍数的数各个位上的数相加所得的和能被3整除,判断出5□中最大填多少时这个数能被3整除;然后根据找一个数的因数,可以一对一对的找,把求出的数写成两个数的乘积,那么每一个乘积中的因数都是它的因数,然后从小到大依次写出即可.
【解答】解:5□中最大填7时这个数能被3整除,
因为57=1×57=3×19,
所以57的因数有:1、3、19、57.
故答案为:7;1、3、19、57.
【点评】此题主要考查了是3的倍数的数的特征,以及找一个数的因数的方法,要熟练掌握.
12.【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位;据此解答.
【解答】解:二十三亿九千七百万是由2个十亿,3个亿,9个千万和7个百万组成的;
故答案为:十亿,亿,千万,百万.
【点评】此题考查整数中的数字所表示的意义:有几个计数单位;解答时一定要看清数位和这个数位的计数单位.
13.【分析】求一个数的因数,就是用这个数除以小于等于这个数的自然数(0除外),能够除尽的自然数就是这个数的因数;求一个数的倍数,就是让这个数乘自然数1、2、3……得出来的积就是这个数的倍数.
【解答】解:24的所有因数有:1、2、3、4、6、8、12、24;50以内7的所有倍数:7、14、21、28、35、42、49.
故答案为:1、2、3、4、6、8、12、24;7、14、21、28、35、42、49.
【点评】此题考查了因数的特点及求法,倍数的特点及求法,注意平时基础知识的积累.
14.【分析】根据质数、偶数的意义,一个数如果只有1和它本身两个因数,这样的数叫做质数,在自然数中,是2的倍数的数叫做偶数.在一位数中,最小的质数是2,最大的偶数8,据此解答.
【解答】解:在一位数中,最小的质数是2,最大的偶数8,2×8=16,
故答案为:16.
【点评】此题考查的目的是理解质数、偶数的意义.
15.【分析】首先根据题意,把所求的重量看作单位“1”,则60吨占所求的重量的(1﹣=);再根据分数除法的意义,用60除以它占所求的重量的分率即可;
然后根据题意,把36kg看作单位“1”,然后根据分数乘法的意义,用36乘所求的重量占36kg的分率即可.
【解答】解:60÷(1﹣)
=60÷
=80(吨)
所以60吨比80吨少;
36×(1+)
=36×
=48(kg)
所以比36kg多是48kg.
故答案为:80、48.
【点评】此题主要考查了分数乘法、分数除法的运算方法,要熟练掌握,注意弄清楚题中的各个量之间的数量关系.
16.【分析】先把、83%、都化成小数,再根据小数比较大小的方法进行比较.
【解答】解:≈0.8333、
83%=0.83、
≈0.875
0.875>0.833>0.83>0.8
即:>>83%>0.8.
故答案为:>>83%>0.8.
【点评】比较不同形式数的大小,一般先都化成小数,再根据小数比较大小的方法求解.
17.【分析】①②通分计算;③约分计算;④⑥⑧把除法改为乘法,再计算;⑤⑦把百分数化为分数计算.
【解答】解:
= = = 2=7
1﹣35%= = = 1=1000
【点评】此题考查了在计算中运用通分、约分、数字转化等知识进行计算的能力.
18.【分析】100个的和相加,属于求几个相同加数和的运算,用乘法计算即可.
【解答】解:
=×100
=37.5
故答案为:37.5.
【点评】此题考查了分数乘整数的意义:求几个相同加数和的简便运算.
19.【分析】首先根据题意,把全书的页数看作单位“1”,根据分数乘法的意义,用全书的页数乘第一周看的占的分率,求出第一周看了多少页;然后根据题意,把第一周看的页数看作单位“1”,根据分数乘法的意义,用第一周的页数乘第二周看的占第一周的分率,求出第二周看了多少页即可.
【解答】解:340××
=85×
=136(页)
答:第二周看了136页.
故答案为:136.
【点评】此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是要明确:求一个数的几分之几是多少,用乘法解答.
20.【分析】先用第一根绳子的长度减去米,求出另一根的长度,再把两根的长度相加即可求解.
【解答】解:﹣+
=++
=﹣
=(米)
答:两根绳子共长米.
故答案为:.
【点评】解决本题根据加减法的意义进行求解即可.
三.判断题(共5小题)
21.【分析】举个反例证明.3的倍数的特征:各个数位上的数的和是3的倍数,这个数就是3的倍数.
【解答】解:13、16、29是个位上分别是3、6、9,可是它们都不是3的倍数,
所以个位上是3、6、9的数,一定是3的倍数的说法是错误的.
故答案为:×.
【点评】本题主要考查3的倍数的特征.注意个位上是3、6、9的数不一定是3的倍数,各个数位上的数的和是3的倍数,这个数就是3的倍数.
22.【分析】本题即求2、3、5、6的最小公倍数,因为2、3的最小公倍数是6,所以只要求出5、6的最小公倍数即可判断.
【解答】解:因为2、3的最小公倍数是6,所以只要求出5、6的最小公倍数,
5×6=30
即同时是2、3、5、6倍数的最小的数是30,所以本题说法错误;
故答案为:×.
【点评】此题实际上就是求2、3、5、6的最小公倍数.
23.【分析】分子大于或等于分母的分数是假分数,假分数大于或等于1,分子小于分母的分数是真分数,真分数小于1.据此解答.
【解答】解:因假分数大于或等于1,真分数小于1,扬眉假分数一定大于真分数.
故答案为:√.
【点评】本题主要考查了学生对真分数和假分数意义的掌握情况.
24.【分析】1﹣,把1变为4个,再减去1个,即可得到剩下3个,从而求解.
【解答】解:1﹣,就是4个减去1个,剩下3个,等于.
故答案为:√.
【点评】考查了分数的减法运算,关键是把1变为4个再相减.
25.【分析】先把全班的总人数看成单位“1”,它的的就是×=,由此进行判断即可.
【解答】解:×=
全班人数的的就是全班人数的
所以原题说法正确;
故答案为:√.
【点评】本题考查了一个数乘分数的意义:求这个数的几分之几是多少.
四.计算题(共2小题)
26.【分析】质数有2、3、5、7、11、13、17…,设其中一个质数为x,另一个质数为y,根据等量关系:一个质数的3倍与另一个质数的2倍之和等于100即可列出一个二元一次方程,求得符合题意的整数解即可解决问题.
【解答】解:设其中一个质数为x,另一个质数为y,根据题意可得方程:
3x+2y=100
y=
根据上式特点可知,要使y有整数解,x必须是偶数,
因为所有的质数中,只有2是偶数,所以这个方程的整数解只有一组:
当x=2时,y=47;
答:这两个质数是2和47.
【点评】此题要考查了质数的性质的灵活应用,特别是解这个二元一次方程时,紧扣能被2整除的数的特征和质数的特点,是解这个不定方程的关键.此题要考查了质数的性质的灵活应用,特别是解这个二元一次方程时,紧扣能被2整除的数的特征和质数的特点,是解这个不定方程的关键.
27.【分析】根据分数减法和乘除法的计算方法直接口算即可.
【解答】解:÷=
1﹣=
3×=
6×=4
【点评】此题考查了学生的口算能力,属于基础题,细心计算即可解答.
五.操作题(共1小题)
28.【分析】根据异分母的分数加减法的计算方法,表示把一个圆平均分成8份,表示3份,表示把一个圆平均分成4份,表示1份;先涂色表示分数,再通分,然后再根据同分母分数加减法的计算方法进行计算.
【解答】解:
【点评】异分母相加减,先通分,化成同分母后,再按同分母分数加减法进行计算.
六.应用题(共5小题)
29.【分析】此题实际上就是求2,3,4的最小公倍数,这个最小公倍数就是他们在起点第一次相遇的时间;据此解答即可.
【解答】解:因为4是2的倍数,4和3互质,
所以,3×4=12(分钟)
答:12分后,亮亮和爸爸、妈妈在起点第一次相遇.
【点评】本题考查了公倍数应用题,考查了学生运用求最小公倍数的方法解决行程问题的能力.
30.【分析】首先根据题意,把1天(24小时)看作单位“1”,然后根据分数乘法的意义,用24乘,求出1天的是多少小时即可.
【解答】解:1天=24小时
24×=20(小时)
答:1天的是20小时.
【点评】此题主要考查了分数乘法的意义的应用,要熟练掌握,解答此题的关键是要明确:求一个数的几分之几是多少,用乘法解答.
31.【分析】根据奇数与偶数、质数与合数的意义,是2的倍数的数叫做偶数.不是2的倍数的数叫做奇数,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.一个自然数,如果除了1和它本身还有别的因数,这样的数叫做合数.先找出20以内的质数,然后把它们分别加上2,然后看得数既是奇数又是合数的,由此解答.
【解答】解:质数有:2,3,5,7,11,13,17,19;
加上2后:
2+2=4
3+2=5
5+2=7
7+2=9
11+2=13
13+2=15
17+2=19
19+2=21
因为加上2后既是奇数又是合数9,15,21;
所以符合要求的质数是:7,13,19;
答:这三个人分别是7岁、13岁、19岁.
【点评】此题考查的目的是使学生理解和掌握奇数与偶数、质数与合数的概念及意义.
32.【分析】依据分数基本性质,把三个洲占陆地面积通分为分母为75的分数,再依据同分母分数大小比较方法即可解答.
【解答】解:==
因为:>>
所以:>>.
答:亚洲的陆地面积最大,南美洲的陆地面积最少.
【点评】本题考查知识点:依据分数基本性质正确解决问题.
33.【分析】把合唱队的人数看成单位“1”,舞蹈队的人数比合唱队多,那么舞蹈队的人数就是合唱队的(1+),用合唱队的人数乘上这个分率,就是舞蹈队的人数.
【解答】解:60×(1+)
=60×
=75(人)
答:参加舞蹈队的有75人.
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法计算.
同课章节目录
