10.4 简单线性规划(2):36张PPT
文档属性
| 名称 | 10.4 简单线性规划(2):36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 00:00:00 | ||
图片预览











文档简介
课件36张PPT。第10章——不等式[学习目标]
1.了解线性规划的意义以及可行解、可行域、最优解等基本概念.
2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题.10.4 简单线性规划(二)1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
已知1≤x+y≤5,-1≤x-y≤3,求2x-3y的取值范围.解答时容易错误的利用不等式中的加法法则,由原不等式组得到x,y的范围,再分别求出2x及-3y的范围,然后相加得2x-3y的取值范围.由于不等式中的加法法则不具有可逆性,从而使x,y的取值范围扩大,得出错误的2x-3y的取值范围.如果把1≤x+y≤5,-1≤x-y≤3看作变量x,y满足的条件,把求2x-3y的取值范围看作在满足上述不等式的情况下,求z=2x-3y的取值范围,就成了本节要研究的一个线性规划问题.[预习导引]
1.线性规划中的基本概念线性约束条件可行解最大值或最小值线性约束2.目标函数的最值当b>0,截距最大时,z取得 值,截距最小时,z取得 值;
当b<0,截距最大时,z取得 值,截距最小时,z取得 值.互相平行最大最大最小最小要点一 求线性目标函数的最值(1)求函数u=3x-y的最大值和最小值;图(1)由u=3x-y,得y=3x-u,得到斜率为3,在y轴上的截距为-u,随u变化的一组平行线,
由图可知,当直线经过可行域上的C点时,截距-u最大,即u最小.∴umin=3×(-2)-3=-9.当直线经过可行域上的B点时,截距-u最小,即u最大,∴umax=3×2-1=5.
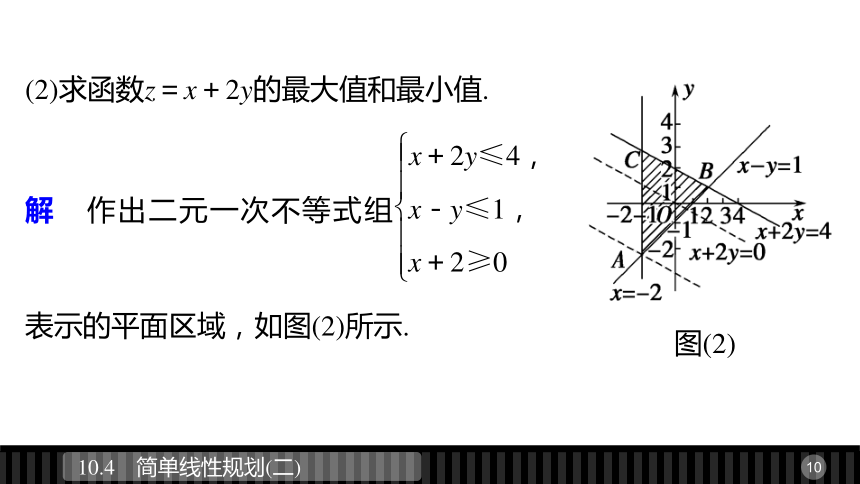
∴u=3x-y的最大值是5,最小值是-9.(2)求函数z=x+2y的最大值和最小值.图(2)∴zmin=-2+2×(-3)=-8.图(2)∴zmax=x+2y=4,
∴z=x+2y的最大值是4,最小值是-8.
规律方法 图解法是解决线性规划问题的有效方法.其关键在于平移目标函数对应的直线ax+by=0,看它经过哪个点(或哪些点)时最先接触可行域和最后离开可行域,则这样的点即为最优解,再注意到它的几何意义,从而确定是取得最大值还是最小值.则z=2x+y的最大值等于( )
A.7 B.8
C.10 D.11解析 作出约束条件下的可行域如图(阴影部分),当直线y=-2x+z经过点A(4,2)时,z取最大值为10.
答案 C要点二 非线性目标函数的最值问题(1)求z=x2+y2-10y+25的最小值;
解 作出可行域如图所示,A(1,3),B(3,1),C(7,9).z=x2+(y-5)2表示可行域内任一点(x,y)到点M(0,5)的距离的平方,
过M作AC的垂线,易知垂足在AC上,规律方法 非线性目标函数的最值问题,要充分理解非线性目标函数的几何意义,诸如两点间的距离(的平方),点到直线的距离,过已知两点的直线斜率等.
常见代数式的几何意义主要有:这些代数式的几何意义能使所求问题得以转化,往往是解决问题的关键.所表示的平面区域,x2+(y+2)2=1所表示的曲线为以(0,-2)为圆心,1为半径的一个圆.要点三 线性规划的实际应用
例3 某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?解 设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,则依题意得:z=2.5x+4y,且x,y满足让目标函数表示的直线2.5x+4y=z在可行域上平移.由此可知z=2.5x+4y在B(4,3)处取得最小值.
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
规律方法 线性规划解决实际问题的步骤:①分析并将已知数据列出表格;②确定线性约束条件;③确定线性目标函数;④画出可行域;⑤利用线性目标函数(直线)求出最优解; ⑥实际问题需要整数解时,应适当调整,以确定最优解.跟踪演练3 某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品,甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为( )A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱甲、乙两车间每天总获利为z=280x+200y.画出可行域如图所示.
点M(15,55)为直线x+y=70和直线10x+6y=480的交点,由图象知在点M(15,55)处z取得最大值.
答案 B12341234答案 C1234A.6 B.7 C.8 D.23
解析 作出可行域如图所示,由图可知,z=2x+3y经过点A(2,1)时,z=2x+3y的最小值为zmin=2×2+3×1=7.B12343.在如图所示的坐标平面的可行域内(阴影部分且包括边界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( )
A.-3 B.3 C.-1 D.11234解析 当a>0或a=0时,取最小值的最优解只有一个,不满足题意,∴a=-3.
答案 A1234解析 由不等式组表示的可行域知,目标函数z在点(0,2)处取得最大值8.8课堂小结
1.用图解法解决线性或非线性规划问题的基本步骤:
(1)在平面直角坐标系内作出可行域.
(2)考虑目标函数的几何意义,将目标函数进行变形.
(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解.
(4)求最值:将最优解代入目标函数即可求出最大值或最小值.2.作不等式组表示的可行域时,注意标出相应的直线方程,还要给可行域的各顶点标上字母,平移直线时,要注意线性目标函数的斜率与可行域中边界直线的斜率进行比较,确定最优解.
3.在解决与线性规划相关的问题时,首先考虑目标函数的几何意义,利用数形结合方法可迅速解决相关问题.
1.了解线性规划的意义以及可行解、可行域、最优解等基本概念.
2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题.10.4 简单线性规划(二)1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
已知1≤x+y≤5,-1≤x-y≤3,求2x-3y的取值范围.解答时容易错误的利用不等式中的加法法则,由原不等式组得到x,y的范围,再分别求出2x及-3y的范围,然后相加得2x-3y的取值范围.由于不等式中的加法法则不具有可逆性,从而使x,y的取值范围扩大,得出错误的2x-3y的取值范围.如果把1≤x+y≤5,-1≤x-y≤3看作变量x,y满足的条件,把求2x-3y的取值范围看作在满足上述不等式的情况下,求z=2x-3y的取值范围,就成了本节要研究的一个线性规划问题.[预习导引]
1.线性规划中的基本概念线性约束条件可行解最大值或最小值线性约束2.目标函数的最值当b>0,截距最大时,z取得 值,截距最小时,z取得 值;
当b<0,截距最大时,z取得 值,截距最小时,z取得 值.互相平行最大最大最小最小要点一 求线性目标函数的最值(1)求函数u=3x-y的最大值和最小值;图(1)由u=3x-y,得y=3x-u,得到斜率为3,在y轴上的截距为-u,随u变化的一组平行线,
由图可知,当直线经过可行域上的C点时,截距-u最大,即u最小.∴umin=3×(-2)-3=-9.当直线经过可行域上的B点时,截距-u最小,即u最大,∴umax=3×2-1=5.
∴u=3x-y的最大值是5,最小值是-9.(2)求函数z=x+2y的最大值和最小值.图(2)∴zmin=-2+2×(-3)=-8.图(2)∴zmax=x+2y=4,
∴z=x+2y的最大值是4,最小值是-8.
规律方法 图解法是解决线性规划问题的有效方法.其关键在于平移目标函数对应的直线ax+by=0,看它经过哪个点(或哪些点)时最先接触可行域和最后离开可行域,则这样的点即为最优解,再注意到它的几何意义,从而确定是取得最大值还是最小值.则z=2x+y的最大值等于( )
A.7 B.8
C.10 D.11解析 作出约束条件下的可行域如图(阴影部分),当直线y=-2x+z经过点A(4,2)时,z取最大值为10.
答案 C要点二 非线性目标函数的最值问题(1)求z=x2+y2-10y+25的最小值;
解 作出可行域如图所示,A(1,3),B(3,1),C(7,9).z=x2+(y-5)2表示可行域内任一点(x,y)到点M(0,5)的距离的平方,
过M作AC的垂线,易知垂足在AC上,规律方法 非线性目标函数的最值问题,要充分理解非线性目标函数的几何意义,诸如两点间的距离(的平方),点到直线的距离,过已知两点的直线斜率等.
常见代数式的几何意义主要有:这些代数式的几何意义能使所求问题得以转化,往往是解决问题的关键.所表示的平面区域,x2+(y+2)2=1所表示的曲线为以(0,-2)为圆心,1为半径的一个圆.要点三 线性规划的实际应用
例3 某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?解 设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,则依题意得:z=2.5x+4y,且x,y满足让目标函数表示的直线2.5x+4y=z在可行域上平移.由此可知z=2.5x+4y在B(4,3)处取得最小值.
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
规律方法 线性规划解决实际问题的步骤:①分析并将已知数据列出表格;②确定线性约束条件;③确定线性目标函数;④画出可行域;⑤利用线性目标函数(直线)求出最优解; ⑥实际问题需要整数解时,应适当调整,以确定最优解.跟踪演练3 某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品,甲车间加工一箱原料需耗费工时10小时,可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为( )A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱甲、乙两车间每天总获利为z=280x+200y.画出可行域如图所示.
点M(15,55)为直线x+y=70和直线10x+6y=480的交点,由图象知在点M(15,55)处z取得最大值.
答案 B12341234答案 C1234A.6 B.7 C.8 D.23
解析 作出可行域如图所示,由图可知,z=2x+3y经过点A(2,1)时,z=2x+3y的最小值为zmin=2×2+3×1=7.B12343.在如图所示的坐标平面的可行域内(阴影部分且包括边界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( )
A.-3 B.3 C.-1 D.11234解析 当a>0或a=0时,取最小值的最优解只有一个,不满足题意,∴a=-3.
答案 A1234解析 由不等式组表示的可行域知,目标函数z在点(0,2)处取得最大值8.8课堂小结
1.用图解法解决线性或非线性规划问题的基本步骤:
(1)在平面直角坐标系内作出可行域.
(2)考虑目标函数的几何意义,将目标函数进行变形.
(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解.
(4)求最值:将最优解代入目标函数即可求出最大值或最小值.2.作不等式组表示的可行域时,注意标出相应的直线方程,还要给可行域的各顶点标上字母,平移直线时,要注意线性目标函数的斜率与可行域中边界直线的斜率进行比较,确定最优解.
3.在解决与线性规划相关的问题时,首先考虑目标函数的几何意义,利用数形结合方法可迅速解决相关问题.
