高中数学北师大版必修3课件:第二章 算法初步 本章整合 :44张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:第二章 算法初步 本章整合 :44张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-07 20:40:21 | ||
图片预览








文档简介
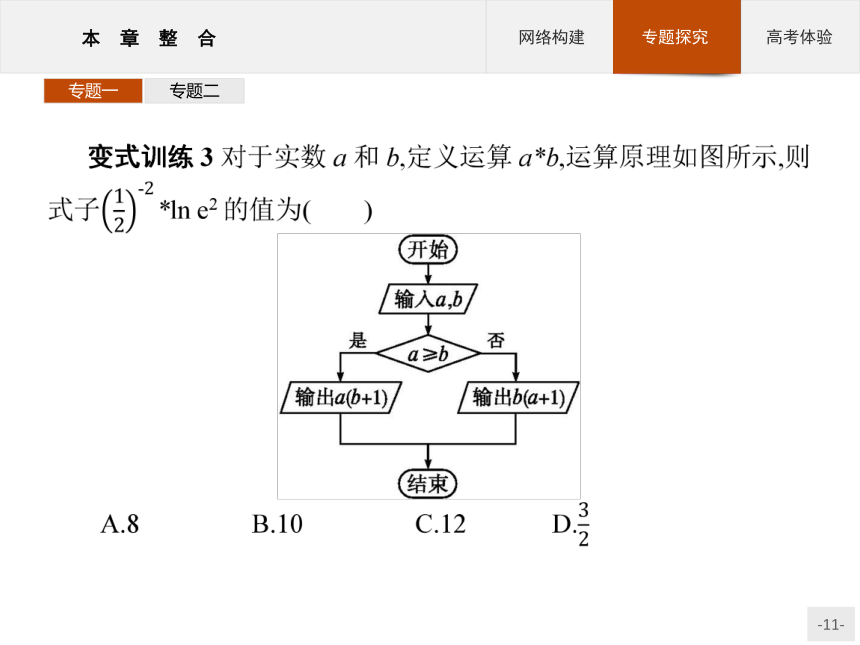
课件44张PPT。本 章 整 合专题一专题二算法框图及其应用
算法框图是算法的一种表示形式,具有直观、形象的特点.高考对算法的考查主要就是考查算法框图的相关问题,主要包括以下几个方面:一是根据算法框图确定输出结果;二是确定算法框图所对应算法的功能;三是根据算法框图的运行结果确定所输入变量的值;四是补充算法框图中缺少的内容.专题一专题二1.确定输出结果
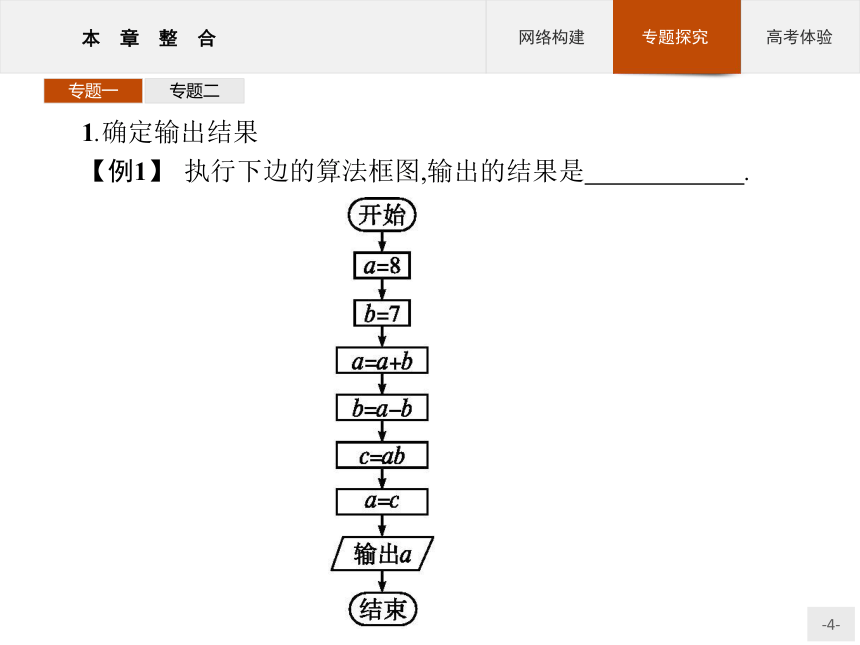
【例1】 执行下边的算法框图,输出的结果是 .?专题一专题二分析:算法框图主要为顺序结构,注意赋值的含义.
解析:由算法框图知:a=8,b=7?a=8+7=15?b=15-7=8
?c=15×8=120?a=120.故输出a=120.
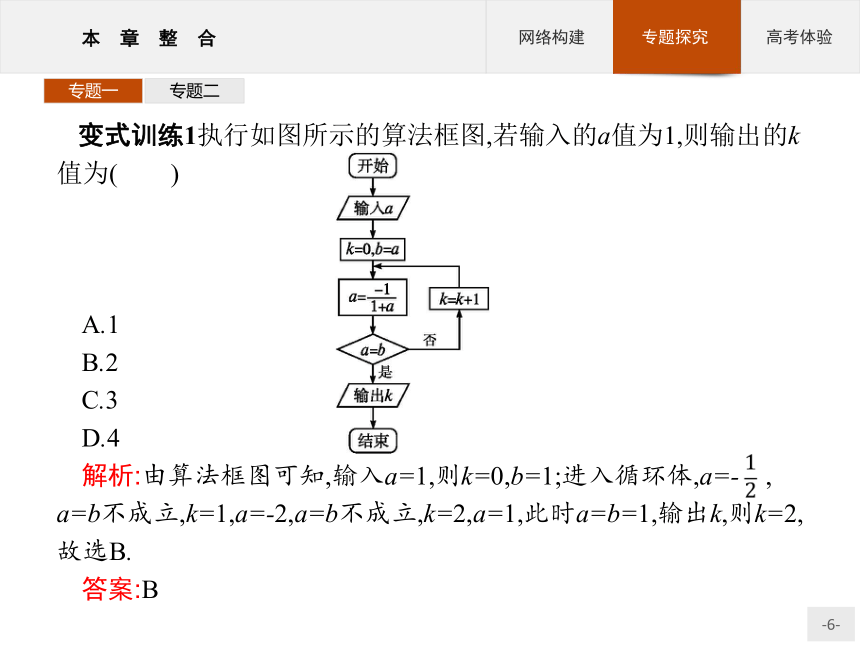
答案:120专题一专题二 变式训练1执行如图所示的算法框图,若输入的a值为1,则输出的k值为( )
?
A.1
B.2
C.3
D.4
解析:由算法框图可知,输入a=1,则k=0,b=1;进入循环体,a=- , a=b不成立,k=1,a=-2,a=b不成立,k=2,a=1,此时a=b=1,输出k,则k=2,故选B.
答案:B专题一专题二【例2】 读下面的算法框图,若输入x的值为-5,则输出的结果是 .?分析:该算法主要运用选择结构设计,注意对输入x的值进行判断.答案:-1 专题一专题二变式训练2执行如图所示的算法框图,输出的结果为( )A.(-2,2) B.(-4,0) C.(-4,-4) D.(0,-8) 专题一专题二解析:x=1,y=1,k=0,
进入循环:s=1-1=0,t=1+1=2,x=0,y=2,k=0+1=1<3;
s=0-2=-2,t=0+2=2,
x=-2,y=2,k=1+1=2<3;s=-2-2=-4,t=-2+2=0,x=-4,y=0,
k=2+1=3≥3,跳出循环,输出(x,y),即(-4,0).
答案:B专题一专题二2.确定算法框图所描述的算法功能
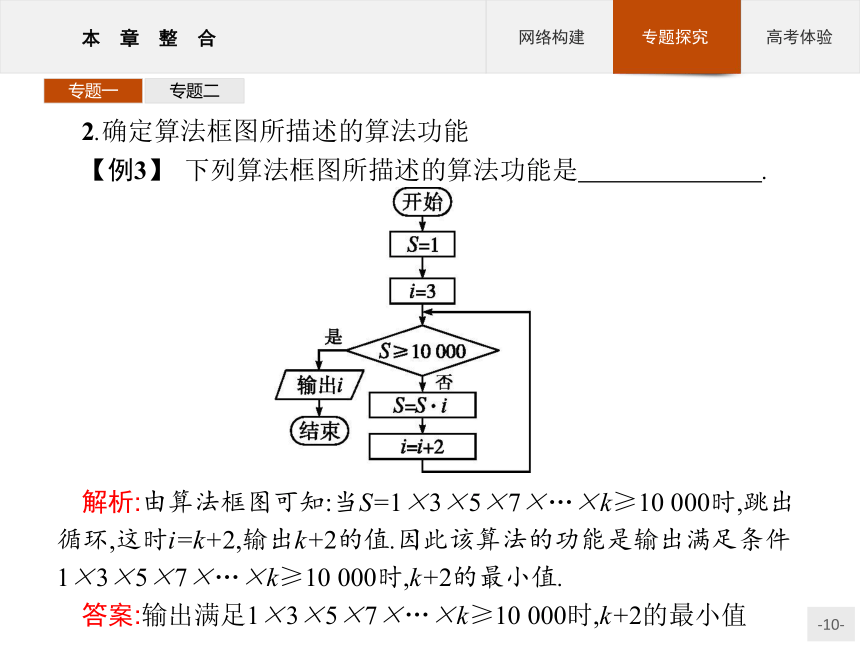
【例3】 下列算法框图所描述的算法功能是 .?解析:由算法框图可知:当S=1×3×5×7×…×k≥10 000时,跳出循环,这时i=k+2,输出k+2的值.因此该算法的功能是输出满足条件1×3×5×7×…×k≥10 000时,k+2的最小值.
答案:输出满足1×3×5×7×…×k≥10 000时,k+2的最小值专题一专题二专题一专题二答案:C 专题一专题二专题一专题二答案:C 专题一专题二 变式训练4阅读如图所示的算法框图,若输出y的值为 ,则输入实数x的值为 .?专题一专题二4.补充算法框图缺少的内容
【例5】 在给出的计算 的值的一个算法框图中,①处和②处应填的语句是( )
A.n=n+2,i>15
B.n=n+2,i=15
C.n=n+1,i=15
D.n=n+1,i>15
解析:这是由循环结构设计的算法框图.
①处应该是对变量n的值进行递增赋值,
即n=n+2;②处应该是进行条件判断,参
与求和共15项,故②处应填i>15.
答案:A专题一专题二变式训练5在某音乐唱片超市里,每张唱片售价12元,顾客若购买5张以上(含5张)唱片,则按照九折收费;若购买10张以上(含10张)唱片,则按照八折收费.请将下面计费的算法框图补充完整.专题一专题二答案:①x<5 ②x<10 ③10.8x 专题一专题二算法与其他知识的融合
算法是一个重要的数学知识交汇点,它可以与其他数学知识充分地融合在一起,体现知识之间的内在联系.算法与函数、方程、不等式、统计等知识都有密切的联系.专题一专题二1.算法与函数融合
【例6】 某算法框图如图所示,现输入如下四个函数,则可以输出的函数是( )解析:由算法框图知输出的函数应该既是奇函数,又存在零点.A项中函数是偶函数,排除A;B项中函数是奇函数,但没有零点,排除B;C项函数是奇函数,也存在零点x=0;D项中的函数f(x)=x3+x2显然不是奇函数.故选C.
答案:C专题一专题二【例7】 在如图所示的算法框图中,若输出y值的范围是[0,10],则输入x的范围是 .?分析:这是一个计算分段函数值的算法框图,写出这个分段函数,根据函数值的范围确定自变量的范围即可.专题一专题二答案:[-7,9] 专题一专题二2.算法与不等式融合
【例8】 执行如图所示的算法框图,若输出k=2,则输入x的取值范围是 .?
分析:本题中的算法框图含有循环结构.由k是计数变量,且当x>115时输出k的值为2,可以列出关于x的不等式组,求之即可.专题一专题二答案:(28,57] 专题一专题二变式训练6执行如图所示的算法框图,输出的n为 .?专题一专题二答案:4 专题一专题二3.算法与统计的融合
【例9】 为了保证人民生命和财产安全,呼吁社会各界共同关注科学睡眠,杜绝疲劳驾驶,某网站针对睡眠问题做了持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.专题一专题二(1)画出频率分布直方图;
(2)为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法框图,求输出的S的值,并说明S的统计意义.专题一专题二解:(1)频率分布直方图如图所示.
?
(2)首先要理解题中算法框图的含义,输入mi,fi的值后,由赋值语句:S=S+mi·fi可知,算法进入一个求和状态.即S=4.5×0.04+5.5×0.26+6.5×0.30+7.5×0.28+8.5×0.10+9.5×0.02=6.70.
则输出的S为6.70.
S的统计意义即是指参加调查者的平均睡眠时间.考点1 顺序结构与选择结构
1.(2017山东高考)执行两次下图所示的算法框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )A.0,0 B.1,1
C.0,1 D.1,0 解析:若输入x=7,则b=2(b2x)→输出a=1;若输入x=9,则b=2(b2答案:D2.(2013课标全国Ⅰ高考)执行右面的算法框图,如果输入的t∈[-1,3],则输出的s属于( )
A.[-3,4] B.[-5,2]
C.[-4,3] D.[-2,5]
解析:当-1≤t<1时,s=3t,则s∈[-3,3).
当1≤t≤3时,s=4t-t2.
∵该函数的对称轴为t=2,
∴该函数在[1,2]上单调递增,在[2,3]上单调递减.
∴smax=4,smin=3.
∴s∈[3,4].
综上知s∈[-3,4].
故选A.
答案:A考点2 循环结构
3.(2018全国2高考)为计算 ,设计了右侧的算法框图,则在空白框中应填入( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4答案:B 4.(2018天津高考)阅读右边的算法框图,运行相应的程序,若输入N的值为20,则输出T的值为( )
A.1
B.2
C.3
D.4答案:B 5.(2017全国3高考)执行下面的算法框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5 B.4
C.3 D.2 解析:程序运行过程如下表所示: 此时S=90<91首次满足条件,程序需在t=3时跳出循环,即N=2为满足条件的最小值,故选D.
答案:D6.(2017全国2高考)执行右面的算法框图,如果输入的a=-1,则输出的S=( )
A.2 B.3
C.4 D.5
解析:算法框图运行如下:
a=-1,S=0,K=1,进入循环,
S=0+(-1)×1=-1,a=1,K=2;
S=-1+1×2=1,a=-1,K=3;
S=1+(-1)×3=-2,a=1,K=4;
S=-2+1×4=2,a=-1,K=5;
S=2+(-1)×5=-3,a=1,K=6;
S=-3+1×6=3,a=-1,K=7,
此时退出循环,输出S=3.故选B.
答案:BA.A>1 000和n=n+1
B.A>1 000和n=n+2
C.A≤1 000和n=n+1
D.A≤1 000和n=n+2答案:D 8.(2016全国乙高考)执行如图所示的算法框图,如果输入的x=0, y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x
C.y=4x D.y=5x
解析:由题图可知,x=0,y=1,n=1,执行如下循环:
x=0,y=1,n=2;答案:C 9.(2016全国甲高考)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的算法框图,执行该算法框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7 B.12
C.17 D.34
解析:由题意,得x=2,n=2,k=0,s=0,
输入a=2,则s=0×2+2=2,k=1,继续循环;
输入a=2,则s=2×2+2=6,k=2,继续循环;
输入a=5,s=6×2+5=17,k=3>2,退出循环,
输出17.故选C.
答案:C10.(2015课标全国Ⅱ高考)如图所示的算法框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该算法框图,若输入的a,b分别为14,18,则输出的a=( )
A.0 B.2 C.4 D.14
解析:由算法框图,得(14,18)→(14,4)→(10,4)→(6,4)→(2,4)→(2,2),则输出的a=2.
答案:B考点3 基本语句
11.(2013陕西高考)根据下列算法语句,当输入x为60时,输出y的值为( )A.25 B.30 C.31 D.61 答案:C
算法框图是算法的一种表示形式,具有直观、形象的特点.高考对算法的考查主要就是考查算法框图的相关问题,主要包括以下几个方面:一是根据算法框图确定输出结果;二是确定算法框图所对应算法的功能;三是根据算法框图的运行结果确定所输入变量的值;四是补充算法框图中缺少的内容.专题一专题二1.确定输出结果
【例1】 执行下边的算法框图,输出的结果是 .?专题一专题二分析:算法框图主要为顺序结构,注意赋值的含义.
解析:由算法框图知:a=8,b=7?a=8+7=15?b=15-7=8
?c=15×8=120?a=120.故输出a=120.
答案:120专题一专题二 变式训练1执行如图所示的算法框图,若输入的a值为1,则输出的k值为( )
?
A.1
B.2
C.3
D.4
解析:由算法框图可知,输入a=1,则k=0,b=1;进入循环体,a=- , a=b不成立,k=1,a=-2,a=b不成立,k=2,a=1,此时a=b=1,输出k,则k=2,故选B.
答案:B专题一专题二【例2】 读下面的算法框图,若输入x的值为-5,则输出的结果是 .?分析:该算法主要运用选择结构设计,注意对输入x的值进行判断.答案:-1 专题一专题二变式训练2执行如图所示的算法框图,输出的结果为( )A.(-2,2) B.(-4,0) C.(-4,-4) D.(0,-8) 专题一专题二解析:x=1,y=1,k=0,
进入循环:s=1-1=0,t=1+1=2,x=0,y=2,k=0+1=1<3;
s=0-2=-2,t=0+2=2,
x=-2,y=2,k=1+1=2<3;s=-2-2=-4,t=-2+2=0,x=-4,y=0,
k=2+1=3≥3,跳出循环,输出(x,y),即(-4,0).
答案:B专题一专题二2.确定算法框图所描述的算法功能
【例3】 下列算法框图所描述的算法功能是 .?解析:由算法框图可知:当S=1×3×5×7×…×k≥10 000时,跳出循环,这时i=k+2,输出k+2的值.因此该算法的功能是输出满足条件1×3×5×7×…×k≥10 000时,k+2的最小值.
答案:输出满足1×3×5×7×…×k≥10 000时,k+2的最小值专题一专题二专题一专题二答案:C 专题一专题二专题一专题二答案:C 专题一专题二 变式训练4阅读如图所示的算法框图,若输出y的值为 ,则输入实数x的值为 .?专题一专题二4.补充算法框图缺少的内容
【例5】 在给出的计算 的值的一个算法框图中,①处和②处应填的语句是( )
A.n=n+2,i>15
B.n=n+2,i=15
C.n=n+1,i=15
D.n=n+1,i>15
解析:这是由循环结构设计的算法框图.
①处应该是对变量n的值进行递增赋值,
即n=n+2;②处应该是进行条件判断,参
与求和共15项,故②处应填i>15.
答案:A专题一专题二变式训练5在某音乐唱片超市里,每张唱片售价12元,顾客若购买5张以上(含5张)唱片,则按照九折收费;若购买10张以上(含10张)唱片,则按照八折收费.请将下面计费的算法框图补充完整.专题一专题二答案:①x<5 ②x<10 ③10.8x 专题一专题二算法与其他知识的融合
算法是一个重要的数学知识交汇点,它可以与其他数学知识充分地融合在一起,体现知识之间的内在联系.算法与函数、方程、不等式、统计等知识都有密切的联系.专题一专题二1.算法与函数融合
【例6】 某算法框图如图所示,现输入如下四个函数,则可以输出的函数是( )解析:由算法框图知输出的函数应该既是奇函数,又存在零点.A项中函数是偶函数,排除A;B项中函数是奇函数,但没有零点,排除B;C项函数是奇函数,也存在零点x=0;D项中的函数f(x)=x3+x2显然不是奇函数.故选C.
答案:C专题一专题二【例7】 在如图所示的算法框图中,若输出y值的范围是[0,10],则输入x的范围是 .?分析:这是一个计算分段函数值的算法框图,写出这个分段函数,根据函数值的范围确定自变量的范围即可.专题一专题二答案:[-7,9] 专题一专题二2.算法与不等式融合
【例8】 执行如图所示的算法框图,若输出k=2,则输入x的取值范围是 .?
分析:本题中的算法框图含有循环结构.由k是计数变量,且当x>115时输出k的值为2,可以列出关于x的不等式组,求之即可.专题一专题二答案:(28,57] 专题一专题二变式训练6执行如图所示的算法框图,输出的n为 .?专题一专题二答案:4 专题一专题二3.算法与统计的融合
【例9】 为了保证人民生命和财产安全,呼吁社会各界共同关注科学睡眠,杜绝疲劳驾驶,某网站针对睡眠问题做了持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.专题一专题二(1)画出频率分布直方图;
(2)为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法框图,求输出的S的值,并说明S的统计意义.专题一专题二解:(1)频率分布直方图如图所示.
?
(2)首先要理解题中算法框图的含义,输入mi,fi的值后,由赋值语句:S=S+mi·fi可知,算法进入一个求和状态.即S=4.5×0.04+5.5×0.26+6.5×0.30+7.5×0.28+8.5×0.10+9.5×0.02=6.70.
则输出的S为6.70.
S的统计意义即是指参加调查者的平均睡眠时间.考点1 顺序结构与选择结构
1.(2017山东高考)执行两次下图所示的算法框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )A.0,0 B.1,1
C.0,1 D.1,0 解析:若输入x=7,则b=2(b2
A.[-3,4] B.[-5,2]
C.[-4,3] D.[-2,5]
解析:当-1≤t<1时,s=3t,则s∈[-3,3).
当1≤t≤3时,s=4t-t2.
∵该函数的对称轴为t=2,
∴该函数在[1,2]上单调递增,在[2,3]上单调递减.
∴smax=4,smin=3.
∴s∈[3,4].
综上知s∈[-3,4].
故选A.
答案:A考点2 循环结构
3.(2018全国2高考)为计算 ,设计了右侧的算法框图,则在空白框中应填入( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4答案:B 4.(2018天津高考)阅读右边的算法框图,运行相应的程序,若输入N的值为20,则输出T的值为( )
A.1
B.2
C.3
D.4答案:B 5.(2017全国3高考)执行下面的算法框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5 B.4
C.3 D.2 解析:程序运行过程如下表所示: 此时S=90<91首次满足条件,程序需在t=3时跳出循环,即N=2为满足条件的最小值,故选D.
答案:D6.(2017全国2高考)执行右面的算法框图,如果输入的a=-1,则输出的S=( )
A.2 B.3
C.4 D.5
解析:算法框图运行如下:
a=-1,S=0,K=1,进入循环,
S=0+(-1)×1=-1,a=1,K=2;
S=-1+1×2=1,a=-1,K=3;
S=1+(-1)×3=-2,a=1,K=4;
S=-2+1×4=2,a=-1,K=5;
S=2+(-1)×5=-3,a=1,K=6;
S=-3+1×6=3,a=-1,K=7,
此时退出循环,输出S=3.故选B.
答案:BA.A>1 000和n=n+1
B.A>1 000和n=n+2
C.A≤1 000和n=n+1
D.A≤1 000和n=n+2答案:D 8.(2016全国乙高考)执行如图所示的算法框图,如果输入的x=0, y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x
C.y=4x D.y=5x
解析:由题图可知,x=0,y=1,n=1,执行如下循环:
x=0,y=1,n=2;答案:C 9.(2016全国甲高考)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的算法框图,执行该算法框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7 B.12
C.17 D.34
解析:由题意,得x=2,n=2,k=0,s=0,
输入a=2,则s=0×2+2=2,k=1,继续循环;
输入a=2,则s=2×2+2=6,k=2,继续循环;
输入a=5,s=6×2+5=17,k=3>2,退出循环,
输出17.故选C.
答案:C10.(2015课标全国Ⅱ高考)如图所示的算法框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该算法框图,若输入的a,b分别为14,18,则输出的a=( )
A.0 B.2 C.4 D.14
解析:由算法框图,得(14,18)→(14,4)→(10,4)→(6,4)→(2,4)→(2,2),则输出的a=2.
答案:B考点3 基本语句
11.(2013陕西高考)根据下列算法语句,当输入x为60时,输出y的值为( )A.25 B.30 C.31 D.61 答案:C
