高中数学北师大版必修3课件:2.2.3 循环结构 :30张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:2.2.3 循环结构 :30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 636.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 16:56:34 | ||
图片预览








文档简介
课件30张PPT。2.3 循环结构1.循环结构
(1)定义:按照一定条件,反复执行某些步骤的算法结构称为循环结构.
(2)相关概念:反复执行的部分,称为循环体;控制着循环的开始和结束的变量,称为循环变量;
用来判断是否继续执行循环体的条件,称为循环的终止条件.
(3)三要素:循环的初始状态、循环体、循环的终止条件.
2.循环结构的设计
用循环结构来描述算法,在画算法框图之前,需要确定的三件事:
(1)确定循环变量和初始条件;
(2)确定算法中反复执行的部分,即循环体;
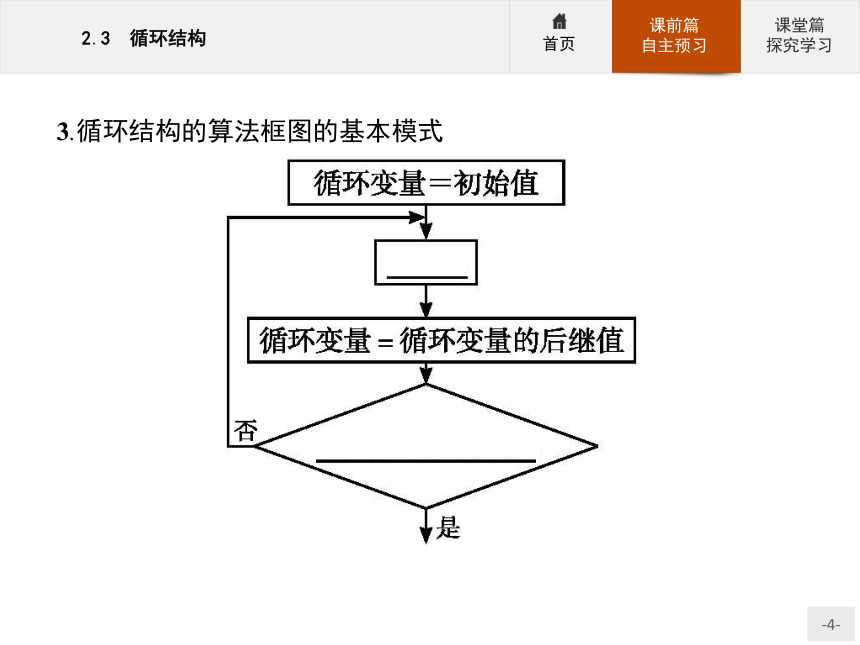
(3)确定循环的终止条件.3.循环结构的算法框图的基本模式 【做一做1】 算法框图中的三种基本逻辑结构是( )
A.顺序结构、选择结构和循环结构
B.输入输出结构、判断结构和循环结构
C.输入输出结构、选择结构和循环结构
D.顺序结构、判断结构和循环结构
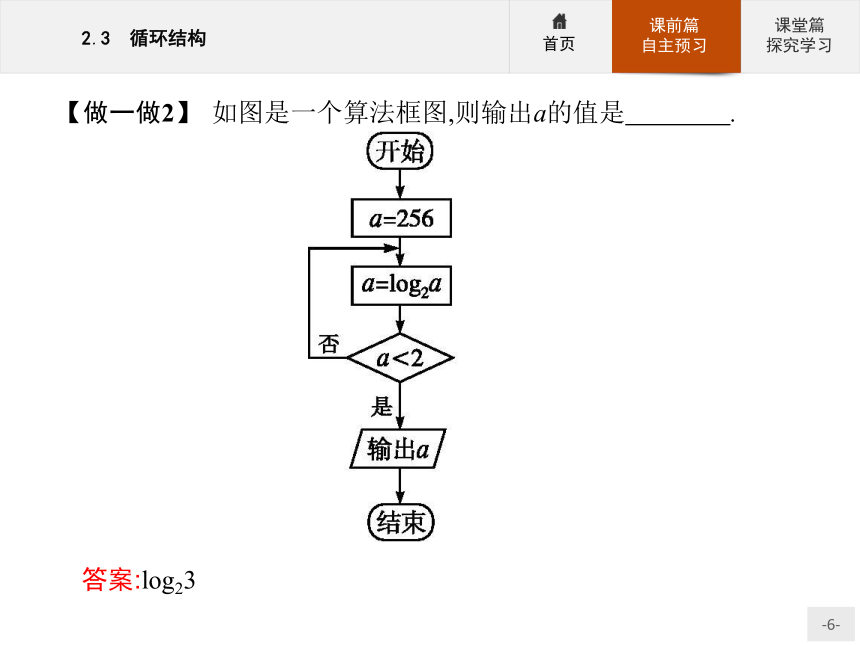
答案:A【做一做2】 如图是一个算法框图,则输出a的值是 .?答案:log23 规律总结算法的三种基本结构的比较 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)循环结构不一定包含选择结构. ( )
(2)每一个算法都离不开顺序结构. ( )
(3)循环结构是在一些算法中从某处开始按照一定条件,反复执行某些处理步骤,因此循环结构一定包含选择结构. ( )
(4)循环结构不能是永不终止的“死循环”,一定要在某一个条件下终止循环. ( )
答案:(1)× (2)√ (3)√ (4)√探究一探究二探究三思想方法当堂检测循环结构算法框图的识图问题
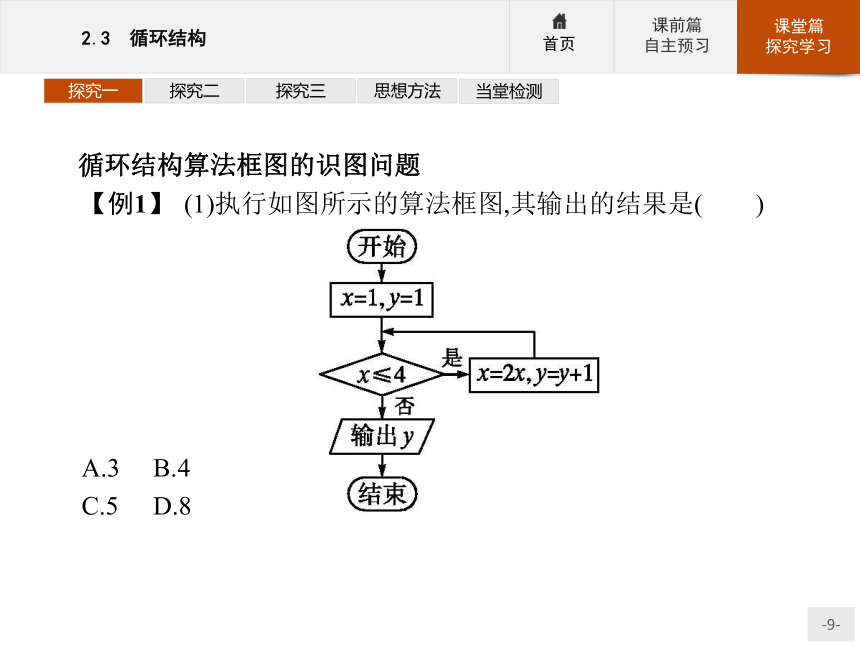
【例1】 (1)执行如图所示的算法框图,其输出的结果是( )
A.3 B.4
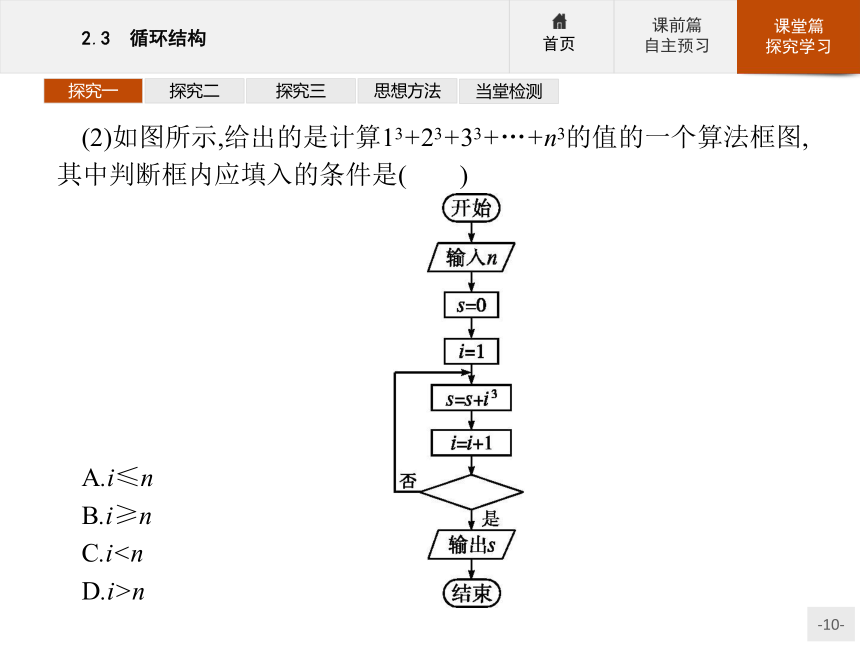
C.5 D.8探究一探究二探究三思想方法当堂检测(2)如图所示,给出的是计算13+23+33+…+n3的值的一个算法框图,其中判断框内应填入的条件是( )
A.i≤n
B.i≥n
C.iD.i>n探究一探究二探究三思想方法当堂检测解析:(1)由算法框图依次可得,x=1,y=1→x=2,y=2→x=4, y=3→x=8,y=4→输出y=4,故选B.
(2)由算法框图可知,当循环终止条件满足时跳出循环,而要计算的是13+23+33+…+n3的值,所以计数变量i=n时应执行循环体,i=n+1时应跳出循环,故应填入的条件是i>n,故选D.
答案:(1)B (2)D探究一探究二探究三思想方法当堂检测反思感悟已知含循环结构的算法框图,分析其算法功能,确定其输出结果,或完善其缺少的内容是一类重要问题,解决这类问题时,应注意以下几点:
(1)明确循环变量、计数变量、循环体分别是什么,尤其要弄清楚循环的次数以及循环终止的条件分别是什么;
(2)若循环执行的次数较少,则可将算法执行过程一一列举、分析获得结果;若循环执行的次数较大,则应考查循环过程中相关变量取值的周期性.探究一探究二探究三思想方法当堂检测变式训练1执行下边的算法框图,若输入的a,b的值分别为0和9,则输出的i的值为 .?探究一探究二探究三思想方法当堂检测解析:第一次循环:a=1,b=8;第二次循环:a=3,b=6;
第三次循环:a=6,b=3;满足条件,结束循环,此时,i=3.
循环结构抓住结束点是关键.
答案:3探究一探究二探究三思想方法当堂检测利用循环结构解决累加、累乘的算法设计问题【例2】 设计一个计算1+2+…+100的值的算法,并画出算法框图.
分析本例题是累加问题,确定计数变量与累计变量后先写出算法,再用框图表示即可.
解算法:
1.令i=1,S=0;
2.S=S+i;
3.i=i+1;
4.若i>100不成立,则返回第二步;
否则,输出S,结束算法.
算法框图如右:探究一探究二探究三思想方法当堂检测反思感悟1.如果算法问题中涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的变化规律,就可以引入变量(称之为循环变量),构成循环结构.
2.在循环结构中,要注意根据条件设计合理的计数变量、累加变量、累乘变量等,特别要求条件的表述要恰当、准确,累加变量的初始值一般取0,累乘变量的初始值一般取1.探究一探究二探究三思想方法当堂检测 变式训练2设计求99×97×95×…×3×1的值的算法,并画出相应的算法框图.
解:算法步骤如下:
1.s=1;
2.i=99;
3.若i≥1,则执行第4步;否则,执行第6步;
4.s=s·i;
5.i=i-2;返回第3步;
6.输出s.
算法框图如图所示.探究一探究二探究三思想方法当堂检测循环结构在实际问题中的应用
【例3】某工厂2018年生产小轿车200万辆,技术革新后预计每年的生产能力比上一年增加5%,问:最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法,并画出相应的算法框图.
分析:由题意,2018年的年产量为200万辆,以后每年的年产量都等于上一年的年产量乘(1+5%),考虑利用循环结构设计算法.探究一探究二探究三思想方法当堂检测解:算法步骤如下:
1.令n=0,a=200,r=0.05;
2.n=n+1;
3.T=ar(计算年增量);
4.a=a+T(计算年产量);
5.若a≤300,则返回重新执行第2步、
第3步、第4步、第5步,否则执行第6步;
6.N=2 018+n;
7.输出N.
算法框图如图所示.探究一探究二探究三思想方法当堂检测反思感悟利用含循环结构的算法框图解决实际问题的方法探究一探究二探究三思想方法当堂检测 变式训练3某班共有学生54人,在一次数学测试中(满分100分),试设计算法筛选出优秀的成绩(85分以上为优秀),并画出程序框图.
解:计数变量用n表示,学生的成绩用r表示.
算法步骤如下:
1.把计数变量n的初始值设为1;
2.输入一个成绩r,比较r与85的大小,
若r>85,则输出r,然后执行下一步;
若r≤85,执行下一步;
3.使计数变量n的值增加1;
4.判断n与54的大小,若n≤54,返回第二步;
若n>54,结束.
程序框图如图所示.探究一探究二探究三思想方法当堂检测程序框图的综合应用
【典例】 画出满足12+22+32+…+n2>2 0182的最小正整数n的算法框图.
分析:不等式左侧是连续正整数的平方和,可用累加法,再根据和的特点设计循环结构进行求解.
解:探究一探究二探究三思想方法当堂检测方法点睛1.无论是累计变量还是循环变量,它们的初始值对循环体都起到了非常重要的作用,因此在解题时,一定要及时检验循环结束时各变量的即时值.
2.注意循环体中处理框与判断框的先后顺序,否则,程序框图的算法功能很可能就要发生变化,不能实现预定的算法结果.探究一探究二探究三思想方法当堂检测变式训练某地区有荒山2 200公顷,从2 018年开始每年年初在荒山上植树造林,第一年植树100公顷,以后每年比上一年多植树50公顷.如图,某同学设计了一个算法框图计算到哪一年可以将荒山全部绿化(假定所植树全部成活),则框图中①处应填上 .?探究一探究二探究三思想方法当堂检测解析:由题意知,荒山的面积是终止循环的条件.故①处应填入S≥2 200.
答案:S≥2 200探究一探究二探究三思想方法当堂检测1.在如图所示的算法框图中,属于循环结构的是( )
?
A.①② B.②③
C.③④ D.②④
解析:①是顺序结构;②中只是对条件的判断,不会重复出现操作;③④属于循环结构.
答案:C探究一探究二探究三思想方法当堂检测2.阅读下面的算法框图,运行相应的程序,则输出i的值为 ( )
A.2 B.3 C.4 D.5
解析:S=10,i=0,
i=i+1=1,S=S-i=10-1=9,不满足S≤1,
i=i+1=2,S=S-i=9-2=7,不满足S≤1,
i=i+1=3,S=S-i=7-3=4,不满足S≤1,
i=i+1=4,S=S-i=4-4=0,满足S≤1,
输出i=4.
答案:C探究一探究二探究三思想方法当堂检测3.已知算法框图如图所示,其输出结果是 .?
解析:a=1,a=2×1+1=3,a>100不成立;a=2×3+1=7,a>100不成立;a=2×7+1=15,a>100不成立;a=2×15+1=31,a>100不成立;a=2×31+1=63,a>100不成立;a=2×63+1=127,a>100成立,输出a=127.
答案:127探究一探究二探究三思想方法当堂检测4.某篮球运动员6场比赛得分如下表.(注:第n场比赛得分为an)在对上述数据进行分析时,一部分计算如算法框图所示(其中 是这6个数据的平均数),则输出的s的值为 .?探究一探究二探究三思想方法当堂检测
(1)定义:按照一定条件,反复执行某些步骤的算法结构称为循环结构.
(2)相关概念:反复执行的部分,称为循环体;控制着循环的开始和结束的变量,称为循环变量;
用来判断是否继续执行循环体的条件,称为循环的终止条件.
(3)三要素:循环的初始状态、循环体、循环的终止条件.
2.循环结构的设计
用循环结构来描述算法,在画算法框图之前,需要确定的三件事:
(1)确定循环变量和初始条件;
(2)确定算法中反复执行的部分,即循环体;
(3)确定循环的终止条件.3.循环结构的算法框图的基本模式 【做一做1】 算法框图中的三种基本逻辑结构是( )
A.顺序结构、选择结构和循环结构
B.输入输出结构、判断结构和循环结构
C.输入输出结构、选择结构和循环结构
D.顺序结构、判断结构和循环结构
答案:A【做一做2】 如图是一个算法框图,则输出a的值是 .?答案:log23 规律总结算法的三种基本结构的比较 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)循环结构不一定包含选择结构. ( )
(2)每一个算法都离不开顺序结构. ( )
(3)循环结构是在一些算法中从某处开始按照一定条件,反复执行某些处理步骤,因此循环结构一定包含选择结构. ( )
(4)循环结构不能是永不终止的“死循环”,一定要在某一个条件下终止循环. ( )
答案:(1)× (2)√ (3)√ (4)√探究一探究二探究三思想方法当堂检测循环结构算法框图的识图问题
【例1】 (1)执行如图所示的算法框图,其输出的结果是( )
A.3 B.4
C.5 D.8探究一探究二探究三思想方法当堂检测(2)如图所示,给出的是计算13+23+33+…+n3的值的一个算法框图,其中判断框内应填入的条件是( )
A.i≤n
B.i≥n
C.i
(2)由算法框图可知,当循环终止条件满足时跳出循环,而要计算的是13+23+33+…+n3的值,所以计数变量i=n时应执行循环体,i=n+1时应跳出循环,故应填入的条件是i>n,故选D.
答案:(1)B (2)D探究一探究二探究三思想方法当堂检测反思感悟已知含循环结构的算法框图,分析其算法功能,确定其输出结果,或完善其缺少的内容是一类重要问题,解决这类问题时,应注意以下几点:
(1)明确循环变量、计数变量、循环体分别是什么,尤其要弄清楚循环的次数以及循环终止的条件分别是什么;
(2)若循环执行的次数较少,则可将算法执行过程一一列举、分析获得结果;若循环执行的次数较大,则应考查循环过程中相关变量取值的周期性.探究一探究二探究三思想方法当堂检测变式训练1执行下边的算法框图,若输入的a,b的值分别为0和9,则输出的i的值为 .?探究一探究二探究三思想方法当堂检测解析:第一次循环:a=1,b=8;第二次循环:a=3,b=6;
第三次循环:a=6,b=3;满足条件,结束循环,此时,i=3.
循环结构抓住结束点是关键.
答案:3探究一探究二探究三思想方法当堂检测利用循环结构解决累加、累乘的算法设计问题【例2】 设计一个计算1+2+…+100的值的算法,并画出算法框图.
分析本例题是累加问题,确定计数变量与累计变量后先写出算法,再用框图表示即可.
解算法:
1.令i=1,S=0;
2.S=S+i;
3.i=i+1;
4.若i>100不成立,则返回第二步;
否则,输出S,结束算法.
算法框图如右:探究一探究二探究三思想方法当堂检测反思感悟1.如果算法问题中涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的变化规律,就可以引入变量(称之为循环变量),构成循环结构.
2.在循环结构中,要注意根据条件设计合理的计数变量、累加变量、累乘变量等,特别要求条件的表述要恰当、准确,累加变量的初始值一般取0,累乘变量的初始值一般取1.探究一探究二探究三思想方法当堂检测 变式训练2设计求99×97×95×…×3×1的值的算法,并画出相应的算法框图.
解:算法步骤如下:
1.s=1;
2.i=99;
3.若i≥1,则执行第4步;否则,执行第6步;
4.s=s·i;
5.i=i-2;返回第3步;
6.输出s.
算法框图如图所示.探究一探究二探究三思想方法当堂检测循环结构在实际问题中的应用
【例3】某工厂2018年生产小轿车200万辆,技术革新后预计每年的生产能力比上一年增加5%,问:最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法,并画出相应的算法框图.
分析:由题意,2018年的年产量为200万辆,以后每年的年产量都等于上一年的年产量乘(1+5%),考虑利用循环结构设计算法.探究一探究二探究三思想方法当堂检测解:算法步骤如下:
1.令n=0,a=200,r=0.05;
2.n=n+1;
3.T=ar(计算年增量);
4.a=a+T(计算年产量);
5.若a≤300,则返回重新执行第2步、
第3步、第4步、第5步,否则执行第6步;
6.N=2 018+n;
7.输出N.
算法框图如图所示.探究一探究二探究三思想方法当堂检测反思感悟利用含循环结构的算法框图解决实际问题的方法探究一探究二探究三思想方法当堂检测 变式训练3某班共有学生54人,在一次数学测试中(满分100分),试设计算法筛选出优秀的成绩(85分以上为优秀),并画出程序框图.
解:计数变量用n表示,学生的成绩用r表示.
算法步骤如下:
1.把计数变量n的初始值设为1;
2.输入一个成绩r,比较r与85的大小,
若r>85,则输出r,然后执行下一步;
若r≤85,执行下一步;
3.使计数变量n的值增加1;
4.判断n与54的大小,若n≤54,返回第二步;
若n>54,结束.
程序框图如图所示.探究一探究二探究三思想方法当堂检测程序框图的综合应用
【典例】 画出满足12+22+32+…+n2>2 0182的最小正整数n的算法框图.
分析:不等式左侧是连续正整数的平方和,可用累加法,再根据和的特点设计循环结构进行求解.
解:探究一探究二探究三思想方法当堂检测方法点睛1.无论是累计变量还是循环变量,它们的初始值对循环体都起到了非常重要的作用,因此在解题时,一定要及时检验循环结束时各变量的即时值.
2.注意循环体中处理框与判断框的先后顺序,否则,程序框图的算法功能很可能就要发生变化,不能实现预定的算法结果.探究一探究二探究三思想方法当堂检测变式训练某地区有荒山2 200公顷,从2 018年开始每年年初在荒山上植树造林,第一年植树100公顷,以后每年比上一年多植树50公顷.如图,某同学设计了一个算法框图计算到哪一年可以将荒山全部绿化(假定所植树全部成活),则框图中①处应填上 .?探究一探究二探究三思想方法当堂检测解析:由题意知,荒山的面积是终止循环的条件.故①处应填入S≥2 200.
答案:S≥2 200探究一探究二探究三思想方法当堂检测1.在如图所示的算法框图中,属于循环结构的是( )
?
A.①② B.②③
C.③④ D.②④
解析:①是顺序结构;②中只是对条件的判断,不会重复出现操作;③④属于循环结构.
答案:C探究一探究二探究三思想方法当堂检测2.阅读下面的算法框图,运行相应的程序,则输出i的值为 ( )
A.2 B.3 C.4 D.5
解析:S=10,i=0,
i=i+1=1,S=S-i=10-1=9,不满足S≤1,
i=i+1=2,S=S-i=9-2=7,不满足S≤1,
i=i+1=3,S=S-i=7-3=4,不满足S≤1,
i=i+1=4,S=S-i=4-4=0,满足S≤1,
输出i=4.
答案:C探究一探究二探究三思想方法当堂检测3.已知算法框图如图所示,其输出结果是 .?
解析:a=1,a=2×1+1=3,a>100不成立;a=2×3+1=7,a>100不成立;a=2×7+1=15,a>100不成立;a=2×15+1=31,a>100不成立;a=2×31+1=63,a>100不成立;a=2×63+1=127,a>100成立,输出a=127.
答案:127探究一探究二探究三思想方法当堂检测4.某篮球运动员6场比赛得分如下表.(注:第n场比赛得分为an)在对上述数据进行分析时,一部分计算如算法框图所示(其中 是这6个数据的平均数),则输出的s的值为 .?探究一探究二探究三思想方法当堂检测
