高中数学人教A版选修 4-4课件:2.2 圆锥曲线的参数方程 :29张PPT
文档属性
| 名称 | 高中数学人教A版选修 4-4课件:2.2 圆锥曲线的参数方程 :29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 917.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 00:00:00 | ||
图片预览







文档简介
课件29张PPT。二 圆锥曲线的参数方程1.椭圆的参数方程 其中OA,OB分别是以原点O为圆心,a,b为半径的圆的半径. 做一做1 椭圆 (φ为参数)的焦距是 .?2.双曲线的参数方程 做一做2 圆锥曲线 (θ为参数)的焦点坐标是( )?
A.(-5,0) B.(5,0)
C.(±5,0) D.(0,±5)答案:C 3.抛物线的参数方程
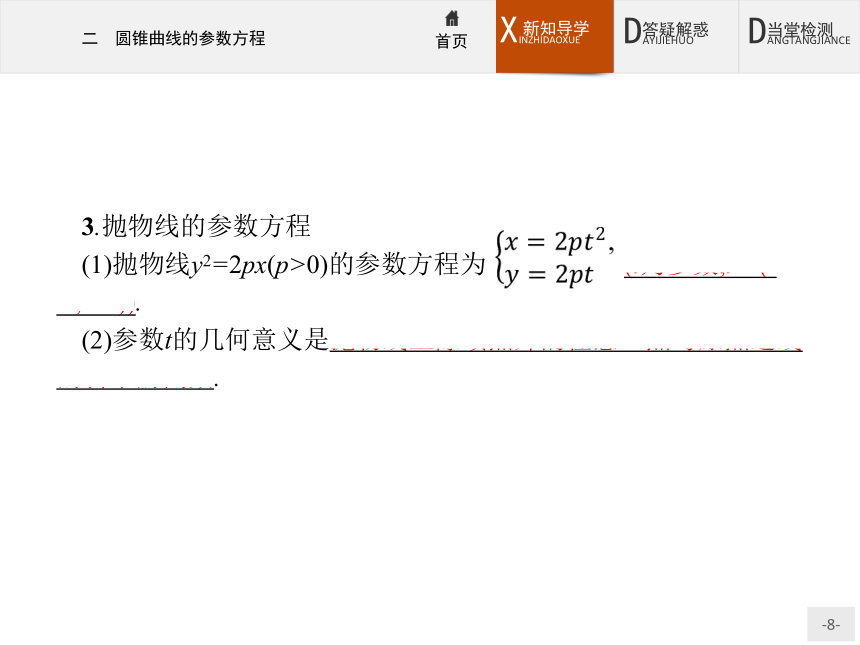
(1)抛物线y2=2px(p>0)的参数方程为 (t为参数,t∈(-∞,+∞)).
(2)参数t的几何意义是抛物线上除顶点外的任意一点与原点连线的斜率的倒数.做一做3 抛物线y2=7x的参数方程为( )? 答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.× √ √ × 探究一探究二探究三思维辨析椭圆的参数方程及其应用?
【例1】 求中心在原点,对称轴为坐标轴,且经过点A(0,5),B(4,0)的椭圆的一个参数方程.
分析:先确定椭圆的焦点所在的位置,再求出普通方程,然后写出参数方程.
解:由题意可知,a=5,b=4,且椭圆的焦点在y轴上,所以椭圆的标准
方程为反思感悟求椭圆的参数方程时,必须确定焦点所在的位置,从而确定普通方程的类型,写出普通方程,然后写出参数方程.探究一探究二探究三思维辨析探究一探究二探究三思维辨析【例2】 已知实数x,y满足 ,求目标函数z=x-2y的最大值与最小值.
分析:将椭圆上的点的坐标设成参数方程的形式,将问题转化成三角函数求最值问题.反思感悟利用椭圆的参数方程,求目标函数的最大(小)值,通常是利用辅助角公式转化为三角函数求解.探究一探究二探究三思维辨析变式训练2 已知A,B分别是椭圆 的右顶点和上顶点,动点C在该椭圆上运动,求△ABC的重心G的轨迹的普通方程.?解:由题意知A(6,0),B(0,3).
由于动点C在椭圆上运动,故可设动点C的坐标为(6cos θ,3sin θ)(θ为参数),点G的坐标为(x,y).探究一探究二探究三思维辨析双曲线的参数方程及其应用?
【例3】 (1)求双曲线 (α为参数)的焦点坐标.
(2)直线AB过双曲线 (a>0,b>0)的中心O,与双曲线交于A,B两点,P是双曲线上的任意一点.求证:直线PA,PB的斜率的乘积为定值.
分析:(1)可将参数方程化为普通方程求解;(2)将曲线上的动点利用双曲线的参数方程设成参数形式,从而将x,y表示成某角θ的函数,然后利用三角函数求解.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟1.对双曲线的参数方程,如果x对应的参数形式是sec φ,则焦点在x轴上;如果y对应的参数形式是sec φ,则焦点在y轴上.
2.对于双曲线而言,它的参数方程主要的应用价值在于:
(1)通过参数(角)简明地表示曲线上任一点的坐标;
(2)将解析几何中的计算问题转化为三角问题,从而运用三角函数的性质及变换公式帮助求解最值、参数的取值范围等;
(3)直线与双曲线位置关系的综合题,可考虑利用双曲线的参数方程设元,再探求解题方法.探究一探究二探究三思维辨析变式训练3?如图,点P为等轴双曲线x2-y2=1上的一点,F1,F2是两个焦点,证明:|PF1|·|PF2|=|OP|2.探究一探究二探究三思维辨析抛物线的参数方程及其应用?【例4】 已知点M为抛物线y2=2x上的动点,定点M0(-1,0),且 ,求点P的轨迹的普通方程.
分析:设出抛物线的参数方程,由定比分点坐标公式得出点P的坐标,消去参数,即得轨迹方程.
解:如图,设M(2t2,2t)(t为参数),P(x,y),探究一探究二探究三思维辨析反思感悟在求曲线的轨迹和研究曲线及方程的相关问题时,常根据需要引入一个中间变量即参数(将x,y表示成关于参数的函数),这种方法是参数法,而涉及曲线上的点的坐标时,可根据曲线的参数方程表示点的坐标.探究一探究二探究三思维辨析变式训练4?过点A(1,0)的直线l与抛物线y2=8x交于M,N两点,求线段MN的中点的轨迹的普通方程.探究一探究二探究三思维辨析对椭圆参数方程中参数的意义理解不清致误 探究一探究二探究三思维辨析数)中,参数φ的意义是不同的.在圆的参数方程中,φ是圆周上的动点M(x,y)所对应的角∠xOM,而椭圆的参数方程中的φ的意义却不是这样的.上述解答把椭圆参数方程中φ的意义错混为圆的参数方程中φ的意义,从而导致了解答的错误.探究一探究二探究三思维辨析1 2 3 4 5答案:C 1 2 3 4 52.曲线 (θ为参数)的长轴长为( )
A.2 B.4 C.6 D.8
解析:将曲线的参数方程化为普通方程,得x2+ =1,它表示焦点在y轴上的椭圆,且其长轴长为4.
答案:B1 2 3 4 5答案:B 1 2 3 4 54.原点到曲线C: (θ为参数)上任意一点的最短距离是 .?解析:曲线C的普通方程为 ,即曲线C为椭圆,且短半轴长b=2.所以所求的最短距离为短半轴长,即为2.
答案:21 2 3 4 55.已知椭圆 ,点A的坐标为(3,0).在椭圆上找一点P,使点P与点A的距离最大.
A.(-5,0) B.(5,0)
C.(±5,0) D.(0,±5)答案:C 3.抛物线的参数方程
(1)抛物线y2=2px(p>0)的参数方程为 (t为参数,t∈(-∞,+∞)).
(2)参数t的几何意义是抛物线上除顶点外的任意一点与原点连线的斜率的倒数.做一做3 抛物线y2=7x的参数方程为( )? 答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.× √ √ × 探究一探究二探究三思维辨析椭圆的参数方程及其应用?
【例1】 求中心在原点,对称轴为坐标轴,且经过点A(0,5),B(4,0)的椭圆的一个参数方程.
分析:先确定椭圆的焦点所在的位置,再求出普通方程,然后写出参数方程.
解:由题意可知,a=5,b=4,且椭圆的焦点在y轴上,所以椭圆的标准
方程为反思感悟求椭圆的参数方程时,必须确定焦点所在的位置,从而确定普通方程的类型,写出普通方程,然后写出参数方程.探究一探究二探究三思维辨析探究一探究二探究三思维辨析【例2】 已知实数x,y满足 ,求目标函数z=x-2y的最大值与最小值.
分析:将椭圆上的点的坐标设成参数方程的形式,将问题转化成三角函数求最值问题.反思感悟利用椭圆的参数方程,求目标函数的最大(小)值,通常是利用辅助角公式转化为三角函数求解.探究一探究二探究三思维辨析变式训练2 已知A,B分别是椭圆 的右顶点和上顶点,动点C在该椭圆上运动,求△ABC的重心G的轨迹的普通方程.?解:由题意知A(6,0),B(0,3).
由于动点C在椭圆上运动,故可设动点C的坐标为(6cos θ,3sin θ)(θ为参数),点G的坐标为(x,y).探究一探究二探究三思维辨析双曲线的参数方程及其应用?
【例3】 (1)求双曲线 (α为参数)的焦点坐标.
(2)直线AB过双曲线 (a>0,b>0)的中心O,与双曲线交于A,B两点,P是双曲线上的任意一点.求证:直线PA,PB的斜率的乘积为定值.
分析:(1)可将参数方程化为普通方程求解;(2)将曲线上的动点利用双曲线的参数方程设成参数形式,从而将x,y表示成某角θ的函数,然后利用三角函数求解.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟1.对双曲线的参数方程,如果x对应的参数形式是sec φ,则焦点在x轴上;如果y对应的参数形式是sec φ,则焦点在y轴上.
2.对于双曲线而言,它的参数方程主要的应用价值在于:
(1)通过参数(角)简明地表示曲线上任一点的坐标;
(2)将解析几何中的计算问题转化为三角问题,从而运用三角函数的性质及变换公式帮助求解最值、参数的取值范围等;
(3)直线与双曲线位置关系的综合题,可考虑利用双曲线的参数方程设元,再探求解题方法.探究一探究二探究三思维辨析变式训练3?如图,点P为等轴双曲线x2-y2=1上的一点,F1,F2是两个焦点,证明:|PF1|·|PF2|=|OP|2.探究一探究二探究三思维辨析抛物线的参数方程及其应用?【例4】 已知点M为抛物线y2=2x上的动点,定点M0(-1,0),且 ,求点P的轨迹的普通方程.
分析:设出抛物线的参数方程,由定比分点坐标公式得出点P的坐标,消去参数,即得轨迹方程.
解:如图,设M(2t2,2t)(t为参数),P(x,y),探究一探究二探究三思维辨析反思感悟在求曲线的轨迹和研究曲线及方程的相关问题时,常根据需要引入一个中间变量即参数(将x,y表示成关于参数的函数),这种方法是参数法,而涉及曲线上的点的坐标时,可根据曲线的参数方程表示点的坐标.探究一探究二探究三思维辨析变式训练4?过点A(1,0)的直线l与抛物线y2=8x交于M,N两点,求线段MN的中点的轨迹的普通方程.探究一探究二探究三思维辨析对椭圆参数方程中参数的意义理解不清致误 探究一探究二探究三思维辨析数)中,参数φ的意义是不同的.在圆的参数方程中,φ是圆周上的动点M(x,y)所对应的角∠xOM,而椭圆的参数方程中的φ的意义却不是这样的.上述解答把椭圆参数方程中φ的意义错混为圆的参数方程中φ的意义,从而导致了解答的错误.探究一探究二探究三思维辨析1 2 3 4 5答案:C 1 2 3 4 52.曲线 (θ为参数)的长轴长为( )
A.2 B.4 C.6 D.8
解析:将曲线的参数方程化为普通方程,得x2+ =1,它表示焦点在y轴上的椭圆,且其长轴长为4.
答案:B1 2 3 4 5答案:B 1 2 3 4 54.原点到曲线C: (θ为参数)上任意一点的最短距离是 .?解析:曲线C的普通方程为 ,即曲线C为椭圆,且短半轴长b=2.所以所求的最短距离为短半轴长,即为2.
答案:21 2 3 4 55.已知椭圆 ,点A的坐标为(3,0).在椭圆上找一点P,使点P与点A的距离最大.
