高中数学人教A版选修 4-1课件:2.3 圆的切线的性质及判定定理 :27张PPT
文档属性
| 名称 | 高中数学人教A版选修 4-1课件:2.3 圆的切线的性质及判定定理 :27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 926.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 21:50:21 | ||
图片预览






文档简介
课件27张PPT。三 圆的切线的性质及判定定理121.切线的性质定理及其推论
(1)性质定理:圆的切线垂直于经过切点的半径.
(2)推论1:经过圆心且垂直于切线的直线必经过切点.
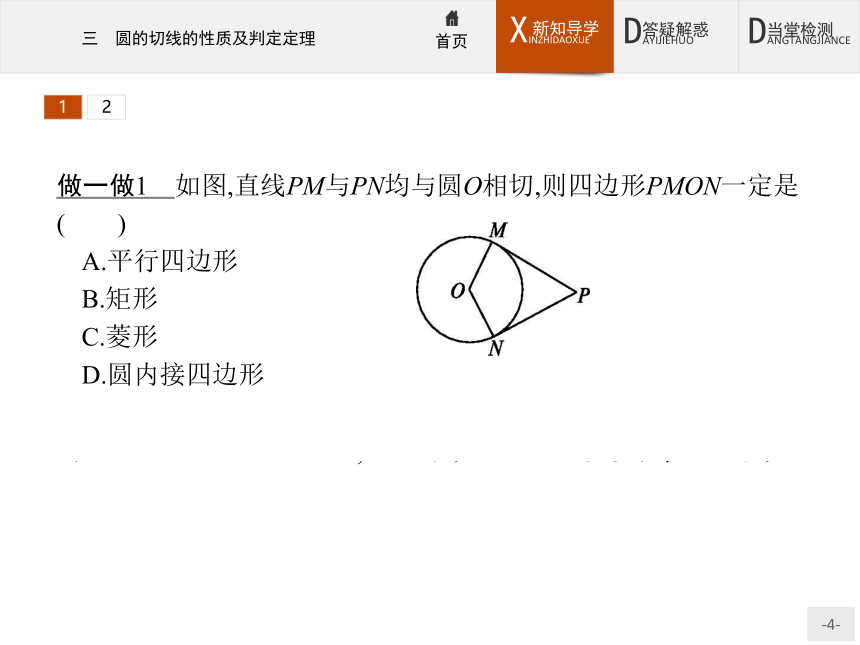
(3)推论2:经过切点且垂直于切线的直线必经过圆心.12做一做1 如图,直线PM与PN均与圆O相切,则四边形PMON一定是( )?
A.平行四边形
B.矩形
C.菱形
D.圆内接四边形
解析因为直线PM与PN均与圆O相切,所以∠PMO=∠PNO=90°,因此∠PMO+∠PNO=180°,故四边形PMON一定是圆内接四边形.
答案D122.切线的判定定理
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.12做一做2?
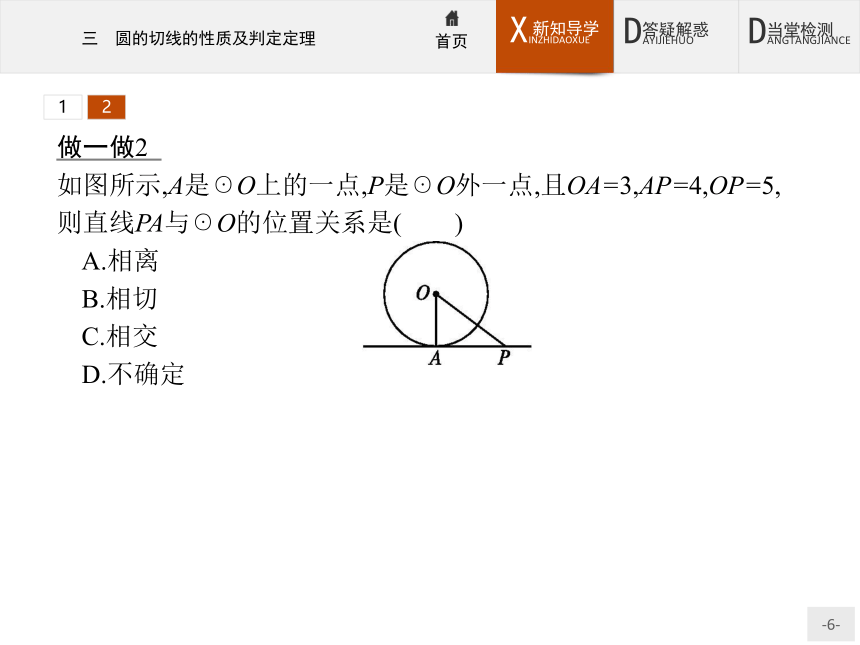
如图所示,A是☉O上的一点,P是☉O外一点,且OA=3,AP=4,OP=5,则直线PA与☉O的位置关系是( )
A.相离
B.相切
C.相交
D.不确定
解析在△OAP中,OA2+AP2=32+42=52=OP2,
∴OA⊥AP,
∴PA与☉O相切.
答案B12思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)垂直于半径的直线是圆的切线. ( )
(2)切线和圆心的距离等于圆的半径. ( )
(3)圆的切线与圆只有一个公共点. ( )
(4)经过直径的一端且垂直于这条直径的直线是圆的切线. ( )
答案(1)× (2)√ (3)√ (4)√探究一探究二探究三探究一圆的切线的判定?
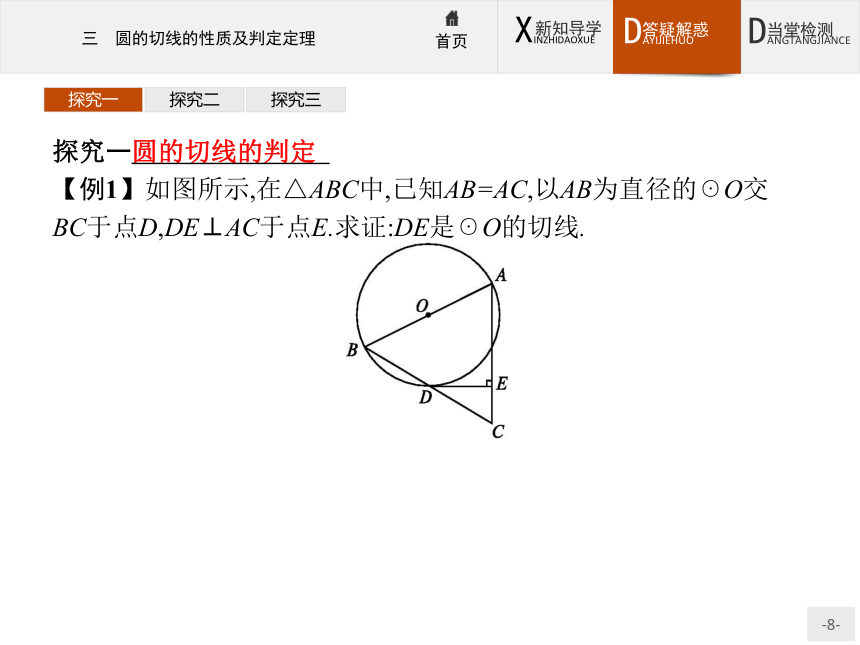
【例1】如图所示,在△ABC中,已知AB=AC,以AB为直径的☉O交BC于点D,DE⊥AC于点E.求证:DE是☉O的切线.
分析利用圆的切线的判定定理进行切线的证明,关键是找出定理的两个条件:(1)过半径的外端;(2)该直线与半径所在的直线垂直.探究一探究二探究三证明
连接OD和AD,如图所示.
∵AB是☉O的直径,∴AD⊥BC.
∵AB=AC,∴BD=CD.
又AO=OB,∴OD是△ABC的中位线,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD,
故DE是☉O的切线.探究一探究二探究三探究一探究二探究三变式训练1 如图所示,△ABC为等腰三角形,
O是底边BC的中点,☉O与腰AB相切于点D.
求证:AC与☉O相切.?证明
连接OD,过点O作OE⊥AC,垂足为E.
∵☉O与AB相切于点D,
∴OD⊥AB,且OD等于圆的半径.
∵△ABC为等腰三角形,O是底边BC的中点,∴∠B=∠C,OB=OC.
又∠ODB=∠OEC=90°,∴△ODB≌△OEC.
∴OE=OD,即OE是☉O的半径,
即圆心O到直线AC的距离等于半径.
故AC与☉O相切.探究一探究二探究三探究二圆的切线的性质?
【例2】 如图所示,AB为☉O的直径,BC,CD为☉O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若☉O的半径为1,求AD·OC的值.
分析(1)要证AD∥OC,因为AB是☉O的直径,所以BD⊥AD.故可转化为证明BD⊥OC;(2)由AD·OC可以联想到△ABD∽△OCB,利用等积式转化线段间的关系.探究一探究二探究三(1)证明
如图,连接OD,BD.
∵BC,CD是☉O的切线,∴OB⊥BC,OD⊥CD.
∴∠OBC=∠ODC=90°.
又∵OB=OD,OC=OC,
∴Rt△OBC≌Rt△ODC.
∴BC=CD.又∵OB=OD,∴OC⊥BD.
∵AB为☉O的直径,∴∠ADB=90°,
即AD⊥BD.∴AD∥OC.
(2)解∵AD∥OC,∴∠A=∠BOC.
又∠ADB=∠OBC=90°,
∴AD·OC=AB·OB=2×1=2.探究一探究二探究三探究一探究二探究三变式训练2?
已知PAB是☉O的割线,AB为☉O的直径,PC为☉O的切线,点C为切点,BD⊥PC交PC延长线于点D,交☉O于点E,PA=AO=OB=1.
(1)求∠P的度数;(2)求DE的长.探究一探究二探究三探究一探究二探究三探究三圆的切线的判定与性质的综合应用?
【例3】
如图所示,已知AP是☉O的切线,P为切点,AC是☉O的割线,与☉O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
(1)证明A,P,O,M四点共圆;
(2)求∠OAM+∠APM的大小.
分析(1)由圆内接四边形的判定定理证明其对角互补即可;(2)由圆周角定理及其推论以及圆的切线的性质进行证明.探究一探究二探究三(1)证明
连接OP,OM,
因为AP与☉O相切于点P,
所以OP⊥AP.因为M是☉O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°.由圆心O在∠PAC的内部,可知四边形APOM的对角互补,
所以A,P,O,M四点共圆.
(2)解 由(1)知,A,P,O,M四点共圆,所以∠OAM=∠OPM.
由(1)知OP⊥AP,而圆心O在∠PAC的内部,可知∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.探究一探究二探究三探究一探究二探究三变式训练3?
如图,已知AB是☉O的直径,DE切☉O于C,并且AD⊥DE于D,BE⊥DE于E.
求证:(1)CD=CE;(2)以C为圆心,CD为半径的☉C和AB相切.探究一探究二探究三证明(1)
如图,连接OC,
∵DE切☉O于C,∴OC⊥DE.
又AD⊥DE,BE⊥DE,
∴AD∥OC∥BE.
∵O为AB的中点,∴CD=CE.
(2)如图,过C点作CF⊥AB于F,过A点作AG⊥OC于G,
∵AD⊥DE,OC⊥DE,AG⊥OC,∴四边形AGCD为矩形,∴AG=CD.
∵OA=OC,∠OGA=∠OFC=90°,∠AOG=∠COF,
∴△AOG≌△COF,∴AG=CF.∴CF=CD,即CF为☉C的半径.又CF⊥AB于F,故☉C与AB相切于点F.123451.已知AB是☉O的切线,在下列给出的条件中,能判定AB⊥CD的是( )
A.AB与☉O相切于直线CD上的点C
B.CD经过圆心O
C.CD是直线
D.AB与☉O相切于C,CD过圆心O
解析由图①②③可知,根据选项A,B,C中的条件都不能判定AB⊥CD;因为圆的切线垂直于经过切点的半径,所以选项D正确(如图④).
答案D123452.如图所示,PB与☉O相切于点B,PO交☉O于点A,BC⊥OP于C,若OA=3 cm,OP=4 cm,则AC等于( )12345解析
答案C123453.如图所示,直线AB与☉O相切于点P,CD是☉O的直径,C,D与AB的距离分别为4 cm,2 cm,则☉O的半径为 .?123454.如图所示,DB,DC是☉O的两条切线,A是圆上一点,已知∠D=46°,则∠A= .?
解析如图所示,连接OB,OC,
则OB⊥BD,OC⊥CD,
故∠DBO+∠DCO=90°+90°=180°,
则四边形OBDC内接于一个圆.
则∠BOC=180°-∠D=180°-46°=134°,
答案67°123455.如图所示,在梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为☉O的直径.求证:☉O与CD相切.
证明 过O作OE⊥CD,垂足为E.
因为AD∥BC,∠C=90°,所以AD∥OE∥BC.
因为O为AB的中点,所以E为CD的中点.
所以☉O与CD相切.
(1)性质定理:圆的切线垂直于经过切点的半径.
(2)推论1:经过圆心且垂直于切线的直线必经过切点.
(3)推论2:经过切点且垂直于切线的直线必经过圆心.12做一做1 如图,直线PM与PN均与圆O相切,则四边形PMON一定是( )?
A.平行四边形
B.矩形
C.菱形
D.圆内接四边形
解析因为直线PM与PN均与圆O相切,所以∠PMO=∠PNO=90°,因此∠PMO+∠PNO=180°,故四边形PMON一定是圆内接四边形.
答案D122.切线的判定定理
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.12做一做2?
如图所示,A是☉O上的一点,P是☉O外一点,且OA=3,AP=4,OP=5,则直线PA与☉O的位置关系是( )
A.相离
B.相切
C.相交
D.不确定
解析在△OAP中,OA2+AP2=32+42=52=OP2,
∴OA⊥AP,
∴PA与☉O相切.
答案B12思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)垂直于半径的直线是圆的切线. ( )
(2)切线和圆心的距离等于圆的半径. ( )
(3)圆的切线与圆只有一个公共点. ( )
(4)经过直径的一端且垂直于这条直径的直线是圆的切线. ( )
答案(1)× (2)√ (3)√ (4)√探究一探究二探究三探究一圆的切线的判定?
【例1】如图所示,在△ABC中,已知AB=AC,以AB为直径的☉O交BC于点D,DE⊥AC于点E.求证:DE是☉O的切线.
分析利用圆的切线的判定定理进行切线的证明,关键是找出定理的两个条件:(1)过半径的外端;(2)该直线与半径所在的直线垂直.探究一探究二探究三证明
连接OD和AD,如图所示.
∵AB是☉O的直径,∴AD⊥BC.
∵AB=AC,∴BD=CD.
又AO=OB,∴OD是△ABC的中位线,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD,
故DE是☉O的切线.探究一探究二探究三探究一探究二探究三变式训练1 如图所示,△ABC为等腰三角形,
O是底边BC的中点,☉O与腰AB相切于点D.
求证:AC与☉O相切.?证明
连接OD,过点O作OE⊥AC,垂足为E.
∵☉O与AB相切于点D,
∴OD⊥AB,且OD等于圆的半径.
∵△ABC为等腰三角形,O是底边BC的中点,∴∠B=∠C,OB=OC.
又∠ODB=∠OEC=90°,∴△ODB≌△OEC.
∴OE=OD,即OE是☉O的半径,
即圆心O到直线AC的距离等于半径.
故AC与☉O相切.探究一探究二探究三探究二圆的切线的性质?
【例2】 如图所示,AB为☉O的直径,BC,CD为☉O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若☉O的半径为1,求AD·OC的值.
分析(1)要证AD∥OC,因为AB是☉O的直径,所以BD⊥AD.故可转化为证明BD⊥OC;(2)由AD·OC可以联想到△ABD∽△OCB,利用等积式转化线段间的关系.探究一探究二探究三(1)证明
如图,连接OD,BD.
∵BC,CD是☉O的切线,∴OB⊥BC,OD⊥CD.
∴∠OBC=∠ODC=90°.
又∵OB=OD,OC=OC,
∴Rt△OBC≌Rt△ODC.
∴BC=CD.又∵OB=OD,∴OC⊥BD.
∵AB为☉O的直径,∴∠ADB=90°,
即AD⊥BD.∴AD∥OC.
(2)解∵AD∥OC,∴∠A=∠BOC.
又∠ADB=∠OBC=90°,
∴AD·OC=AB·OB=2×1=2.探究一探究二探究三探究一探究二探究三变式训练2?
已知PAB是☉O的割线,AB为☉O的直径,PC为☉O的切线,点C为切点,BD⊥PC交PC延长线于点D,交☉O于点E,PA=AO=OB=1.
(1)求∠P的度数;(2)求DE的长.探究一探究二探究三探究一探究二探究三探究三圆的切线的判定与性质的综合应用?
【例3】
如图所示,已知AP是☉O的切线,P为切点,AC是☉O的割线,与☉O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
(1)证明A,P,O,M四点共圆;
(2)求∠OAM+∠APM的大小.
分析(1)由圆内接四边形的判定定理证明其对角互补即可;(2)由圆周角定理及其推论以及圆的切线的性质进行证明.探究一探究二探究三(1)证明
连接OP,OM,
因为AP与☉O相切于点P,
所以OP⊥AP.因为M是☉O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°.由圆心O在∠PAC的内部,可知四边形APOM的对角互补,
所以A,P,O,M四点共圆.
(2)解 由(1)知,A,P,O,M四点共圆,所以∠OAM=∠OPM.
由(1)知OP⊥AP,而圆心O在∠PAC的内部,可知∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.探究一探究二探究三探究一探究二探究三变式训练3?
如图,已知AB是☉O的直径,DE切☉O于C,并且AD⊥DE于D,BE⊥DE于E.
求证:(1)CD=CE;(2)以C为圆心,CD为半径的☉C和AB相切.探究一探究二探究三证明(1)
如图,连接OC,
∵DE切☉O于C,∴OC⊥DE.
又AD⊥DE,BE⊥DE,
∴AD∥OC∥BE.
∵O为AB的中点,∴CD=CE.
(2)如图,过C点作CF⊥AB于F,过A点作AG⊥OC于G,
∵AD⊥DE,OC⊥DE,AG⊥OC,∴四边形AGCD为矩形,∴AG=CD.
∵OA=OC,∠OGA=∠OFC=90°,∠AOG=∠COF,
∴△AOG≌△COF,∴AG=CF.∴CF=CD,即CF为☉C的半径.又CF⊥AB于F,故☉C与AB相切于点F.123451.已知AB是☉O的切线,在下列给出的条件中,能判定AB⊥CD的是( )
A.AB与☉O相切于直线CD上的点C
B.CD经过圆心O
C.CD是直线
D.AB与☉O相切于C,CD过圆心O
解析由图①②③可知,根据选项A,B,C中的条件都不能判定AB⊥CD;因为圆的切线垂直于经过切点的半径,所以选项D正确(如图④).
答案D123452.如图所示,PB与☉O相切于点B,PO交☉O于点A,BC⊥OP于C,若OA=3 cm,OP=4 cm,则AC等于( )12345解析
答案C123453.如图所示,直线AB与☉O相切于点P,CD是☉O的直径,C,D与AB的距离分别为4 cm,2 cm,则☉O的半径为 .?123454.如图所示,DB,DC是☉O的两条切线,A是圆上一点,已知∠D=46°,则∠A= .?
解析如图所示,连接OB,OC,
则OB⊥BD,OC⊥CD,
故∠DBO+∠DCO=90°+90°=180°,
则四边形OBDC内接于一个圆.
则∠BOC=180°-∠D=180°-46°=134°,
答案67°123455.如图所示,在梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为☉O的直径.求证:☉O与CD相切.
证明 过O作OE⊥CD,垂足为E.
因为AD∥BC,∠C=90°,所以AD∥OE∥BC.
因为O为AB的中点,所以E为CD的中点.
所以☉O与CD相切.
