高中数学人教A版选修 4-1课件:1.1 平行线等分线段定理 :26张PPT
文档属性
| 名称 | 高中数学人教A版选修 4-1课件:1.1 平行线等分线段定理 :26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 21:55:43 | ||
图片预览





文档简介
课件26张PPT。第一讲 相似三角形的判定及有关性质
一 平行线等分线段定理1231.平行线等分线段定理
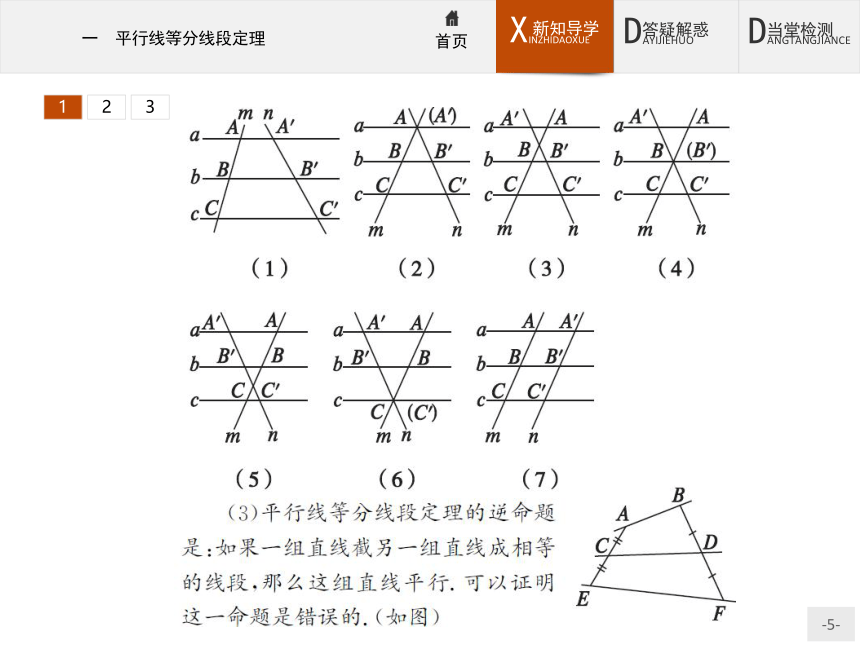
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.123123做一做1 如图所示,已知a∥b∥c,直线AB分别与a,b,c交于点A,E,B,直线CD分别与a,b,c交于点C,E,D,若AE=EB,则( )?
A.AE=CE B.BE=DE
C.CE=DE D.CE>DE
解析由平行线等分线段定理可直接得到答案.
答案C1232.推论1
经过三角形一边的中点与另一边平行的直线必平分第三边.1233.推论2
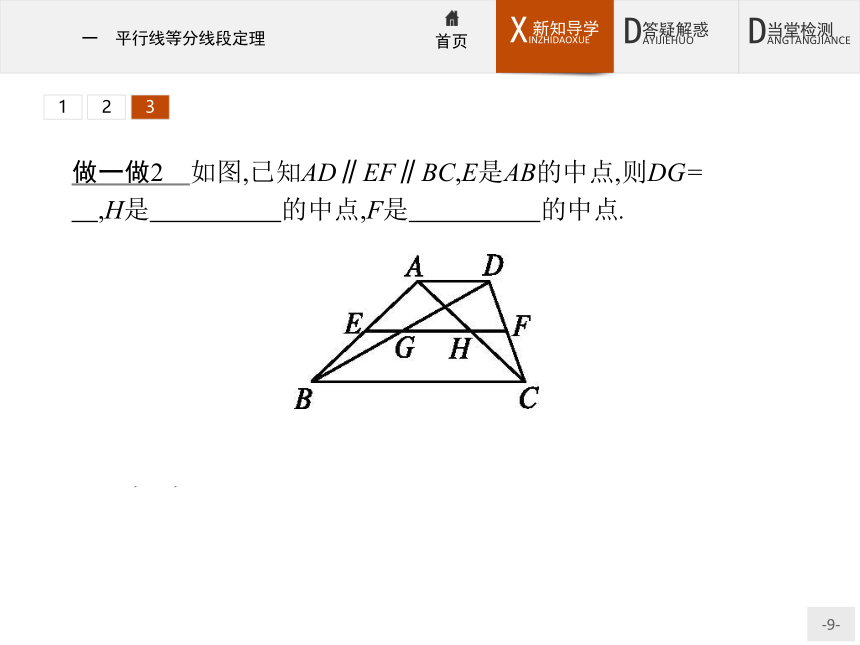
经过梯形一腰的中点,且与底边平行的直线平分另一腰. 123做一做2 如图,已知AD∥EF∥BC,E是AB的中点,则DG= ,H是 的中点,F是 的中点.?
解析由平行线等分线段定理、推论1和2以及AE=EB可得答案,故填BG,AC,CD.
答案BG AC CD123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)如果一组直线在两条直线上截得的线段相等,那么这组直线一定平行. ( )
(2)如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等. ( )
(3)三角形的三条中位线长度的和等于该三角形周长的一半. ( )
(4)梯形的中位线平行于两底,并且等于两底差的一半. ( )
答案(1)× (2)√ (3)√ (4)×探究一探究二探究三探究一作已知线段的等分点?
【例1】 已知线段AB,求作线段AB的六等分点,并予以证明.
分析根据平行线等分线段定理,只要作射线AM,在AM上以任意取定的长度顺次截取6条相等线段,分别设为AA1,A1A2,A2A3,A3A4,A4A5,A5A6,连接端点A6与点B,再过其他端点作BA6的平行线,分别交AB于C,D,E,F,G,则线段AB就被这些平行线分成六等份了.
解(1)任作射线AM(与AB不在同一直线上);
(2)在射线AM上顺次截取AA1=A1A2=A2A3=A3A4=A4A5=A5A6;探究一探究二探究三(3)连接A6B,分别过A1,A2,A3,A4,A5作A6B的平行线A1C,A2D,A3E,A4F,A5G,分别交AB于点C,D,E,F,G,则C,D,E,F,G就是所求作的线段AB的六等分点,如右上图所示.
证明如下:因为A1C∥A2D∥A3E∥A4F∥A5G∥A6B,
又AA1=A1A2=A2A3=A3A4=A4A5=A5A6,
由平行线等分线段定理可得AC=CD=DE=EF=FG=GB,即C,D,E,F,G就是线段AB的六等分点.探究一探究二探究三探究一探究二探究三变式训练1 已知线段AB,在线段AB上求作一点P,使 解如图所示,作法步骤如下:
(1)过点A任作射线AM(与AB不共线);
(2)在AM上以任意长度顺次截取AE=EF=FG;
(3)连接GB,过E,F分别作EP∥GB,FQ∥GB,分别交AB于点P,Q,则点P为所求的点.探究一探究二探究三探究二证明线段相等? 【例2】如图所示,在△ABC中,D是AB的中点,E是BC的三等分点(BE>CE),AE与CD交于点F.求证:DF=FC.
分析过点D作DG∥AE交BC于G,再用平行线等分线段定理证明.探究一探究二探究三证明过点D作DG∥AE交BC于点G.在△ABE中,因为AD=BD,DG∥AE,所以BG=GE.
又因为E是BC的三等分点,所以BG=GE=EC.
在△CDG中,因为GE=CE,DG∥EF,
所以DF=FC.探究一探究二探究三探究一探究二探究三变式训练2 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE∥AB,求证:AE=EC=DE.?
证明因为AB=AC,AD是△ABC的角平分线,所以D为BC的中点.
因为DE∥AB,所以由平行线等分线段定理的推论1知,E为AC的中点,探究一探究二探究三探究三求线段的长度?
【例3】 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,OE∥AB交BC于点E,AD=6,求BE的长.分析由于OE∥AB,OA=OC,根据平行线等分线段定理的推论1,得出E是BC的中点,所以BE=EC探究一探究二探究三解因为四边形ABCD是平行四边形,
所以OA=OC,BC=AD.探究一探究二探究三变式训练3?如图,已知AB∥CD∥EF,AF,BE相交于点O,若AO=OD=DF,BE=10 cm,则OB的长为( )123451.下列用平行线等分线段的图形中,错误的是( )
解析由平行线等分线段定理可知,C项错误.
答案C123452.
如图,在梯形ABCD中,AD∥BC,AD+BC=10 cm,E为AB的中点,点F在DC上,且EF∥AD,则EF的长为( )
A.5 cm B.10 cm
C.20 cm D.不确定
解析由推论2知,EF是梯形ABCD的中位线,
答案A123453.如图所示,若a∥b∥c,那么下列结论中错误的是( )
A.由AB=BC可得FG=GH
B.由AB=BC可得OB=OG
C.由CE=2CD可得CA=2BC
解析由于OB,OG不是一条直线被一组平行线截得的线段,故不一定有OB=OG,即B项错误.
答案B123454.如图所示,已知a∥b∥c,直线m,n分别与直线a,b,c交于点A,B,C和点A',B',C',如果AB=BC=1,A'B'=3,则B'C'= .?
解析由平行线等分线段定理可知A'B'=B'C'.又因为A'B'=3,所以B'C'=3.
答案3123455.如图,在平行四边形ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P,Q两点.求证:AP=PQ=QC.
证明因为四边形ABCD是平行四边形,E,F分别是BC,AD边的中点,
所以DF∥BE,且DF=BE,所以四边形BEDF是平行四边形.
因为在△ADQ中,F是AD的中点,FP∥DQ,
所以P是AQ的中点,所以AP=PQ.
因为在△CPB中,E是BC的中点,EQ∥BP,
所以Q是CP的中点,所以CQ=PQ,故AP=PQ=QC.
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.123123做一做1 如图所示,已知a∥b∥c,直线AB分别与a,b,c交于点A,E,B,直线CD分别与a,b,c交于点C,E,D,若AE=EB,则( )?
A.AE=CE B.BE=DE
C.CE=DE D.CE>DE
解析由平行线等分线段定理可直接得到答案.
答案C1232.推论1
经过三角形一边的中点与另一边平行的直线必平分第三边.1233.推论2
经过梯形一腰的中点,且与底边平行的直线平分另一腰. 123做一做2 如图,已知AD∥EF∥BC,E是AB的中点,则DG= ,H是 的中点,F是 的中点.?
解析由平行线等分线段定理、推论1和2以及AE=EB可得答案,故填BG,AC,CD.
答案BG AC CD123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)如果一组直线在两条直线上截得的线段相等,那么这组直线一定平行. ( )
(2)如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等. ( )
(3)三角形的三条中位线长度的和等于该三角形周长的一半. ( )
(4)梯形的中位线平行于两底,并且等于两底差的一半. ( )
答案(1)× (2)√ (3)√ (4)×探究一探究二探究三探究一作已知线段的等分点?
【例1】 已知线段AB,求作线段AB的六等分点,并予以证明.
分析根据平行线等分线段定理,只要作射线AM,在AM上以任意取定的长度顺次截取6条相等线段,分别设为AA1,A1A2,A2A3,A3A4,A4A5,A5A6,连接端点A6与点B,再过其他端点作BA6的平行线,分别交AB于C,D,E,F,G,则线段AB就被这些平行线分成六等份了.
解(1)任作射线AM(与AB不在同一直线上);
(2)在射线AM上顺次截取AA1=A1A2=A2A3=A3A4=A4A5=A5A6;探究一探究二探究三(3)连接A6B,分别过A1,A2,A3,A4,A5作A6B的平行线A1C,A2D,A3E,A4F,A5G,分别交AB于点C,D,E,F,G,则C,D,E,F,G就是所求作的线段AB的六等分点,如右上图所示.
证明如下:因为A1C∥A2D∥A3E∥A4F∥A5G∥A6B,
又AA1=A1A2=A2A3=A3A4=A4A5=A5A6,
由平行线等分线段定理可得AC=CD=DE=EF=FG=GB,即C,D,E,F,G就是线段AB的六等分点.探究一探究二探究三探究一探究二探究三变式训练1 已知线段AB,在线段AB上求作一点P,使 解如图所示,作法步骤如下:
(1)过点A任作射线AM(与AB不共线);
(2)在AM上以任意长度顺次截取AE=EF=FG;
(3)连接GB,过E,F分别作EP∥GB,FQ∥GB,分别交AB于点P,Q,则点P为所求的点.探究一探究二探究三探究二证明线段相等? 【例2】如图所示,在△ABC中,D是AB的中点,E是BC的三等分点(BE>CE),AE与CD交于点F.求证:DF=FC.
分析过点D作DG∥AE交BC于G,再用平行线等分线段定理证明.探究一探究二探究三证明过点D作DG∥AE交BC于点G.在△ABE中,因为AD=BD,DG∥AE,所以BG=GE.
又因为E是BC的三等分点,所以BG=GE=EC.
在△CDG中,因为GE=CE,DG∥EF,
所以DF=FC.探究一探究二探究三探究一探究二探究三变式训练2 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE∥AB,求证:AE=EC=DE.?
证明因为AB=AC,AD是△ABC的角平分线,所以D为BC的中点.
因为DE∥AB,所以由平行线等分线段定理的推论1知,E为AC的中点,探究一探究二探究三探究三求线段的长度?
【例3】 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,OE∥AB交BC于点E,AD=6,求BE的长.分析由于OE∥AB,OA=OC,根据平行线等分线段定理的推论1,得出E是BC的中点,所以BE=EC探究一探究二探究三解因为四边形ABCD是平行四边形,
所以OA=OC,BC=AD.探究一探究二探究三变式训练3?如图,已知AB∥CD∥EF,AF,BE相交于点O,若AO=OD=DF,BE=10 cm,则OB的长为( )123451.下列用平行线等分线段的图形中,错误的是( )
解析由平行线等分线段定理可知,C项错误.
答案C123452.
如图,在梯形ABCD中,AD∥BC,AD+BC=10 cm,E为AB的中点,点F在DC上,且EF∥AD,则EF的长为( )
A.5 cm B.10 cm
C.20 cm D.不确定
解析由推论2知,EF是梯形ABCD的中位线,
答案A123453.如图所示,若a∥b∥c,那么下列结论中错误的是( )
A.由AB=BC可得FG=GH
B.由AB=BC可得OB=OG
C.由CE=2CD可得CA=2BC
解析由于OB,OG不是一条直线被一组平行线截得的线段,故不一定有OB=OG,即B项错误.
答案B123454.如图所示,已知a∥b∥c,直线m,n分别与直线a,b,c交于点A,B,C和点A',B',C',如果AB=BC=1,A'B'=3,则B'C'= .?
解析由平行线等分线段定理可知A'B'=B'C'.又因为A'B'=3,所以B'C'=3.
答案3123455.如图,在平行四边形ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P,Q两点.求证:AP=PQ=QC.
证明因为四边形ABCD是平行四边形,E,F分别是BC,AD边的中点,
所以DF∥BE,且DF=BE,所以四边形BEDF是平行四边形.
因为在△ADQ中,F是AD的中点,FP∥DQ,
所以P是AQ的中点,所以AP=PQ.
因为在△CPB中,E是BC的中点,EQ∥BP,
所以Q是CP的中点,所以CQ=PQ,故AP=PQ=QC.
