高中数学人教A版选修 4-1课件:3.3 平面与圆锥面的截线 :27张PPT
文档属性
| 名称 | 高中数学人教A版选修 4-1课件:3.3 平面与圆锥面的截线 :27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 780.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 21:54:15 | ||
图片预览



文档简介
课件27张PPT。三 平面与圆锥面的截线12341.等腰三角形底边上的高线与一条直线的关系
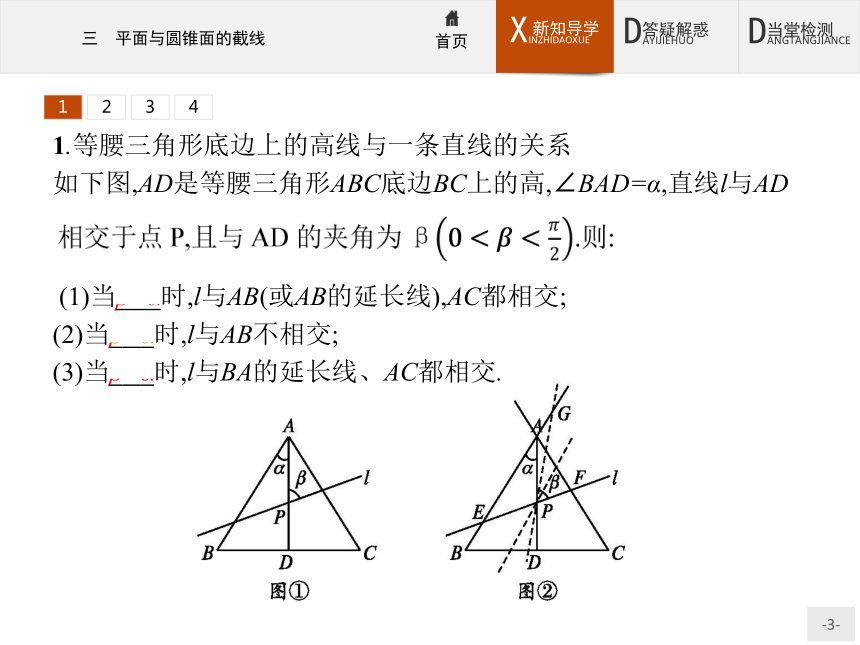
如下图,AD是等腰三角形ABC底边BC上的高,∠BAD=α,直线l与AD
(1)当β>α时,l与AB(或AB的延长线),AC都相交;
(2)当β=α时,l与AB不相交;
(3)当β<α时,l与BA的延长线、AC都相交.12342.定理2
在空间中,取直线l为轴,直线l'与l相交于O点,夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面.任取平面π,若它与轴l的交角为β(当π与l平行时,记β=0),则:
(1)若β>α,则平面π与圆锥的交线为椭圆;
(2)若β=α,则平面π与圆锥的交线为抛物线;
(3)若β<α,则平面π与圆锥的交线为双曲线.1234做一做1 已知圆锥的母线与轴的夹角为50°,一个平面与圆锥轴的夹角为40°,则该平面与圆锥面的截线为 ( )?
A.椭圆 B.圆 C.双曲线 D.抛物线
解析因为α=50°,β=40°,β<α,所以该平面与圆锥面的截线为双曲线.
答案C12343.圆锥曲线的结构特点
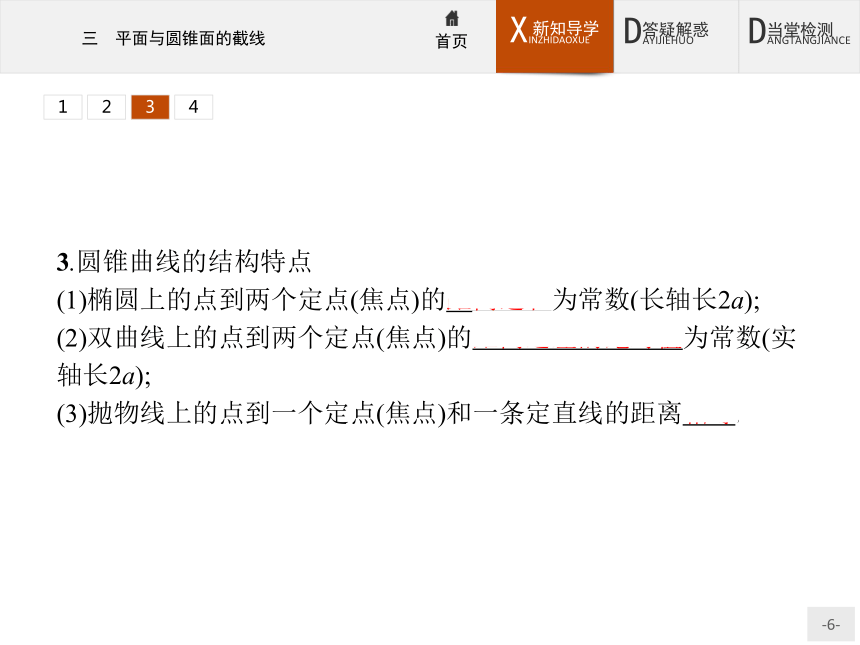
(1)椭圆上的点到两个定点(焦点)的距离之和为常数(长轴长2a);
(2)双曲线上的点到两个定点(焦点)的距离之差的绝对值为常数(实轴长2a);
(3)抛物线上的点到一个定点(焦点)和一条定直线的距离相等.12344.圆锥曲线的几何性质
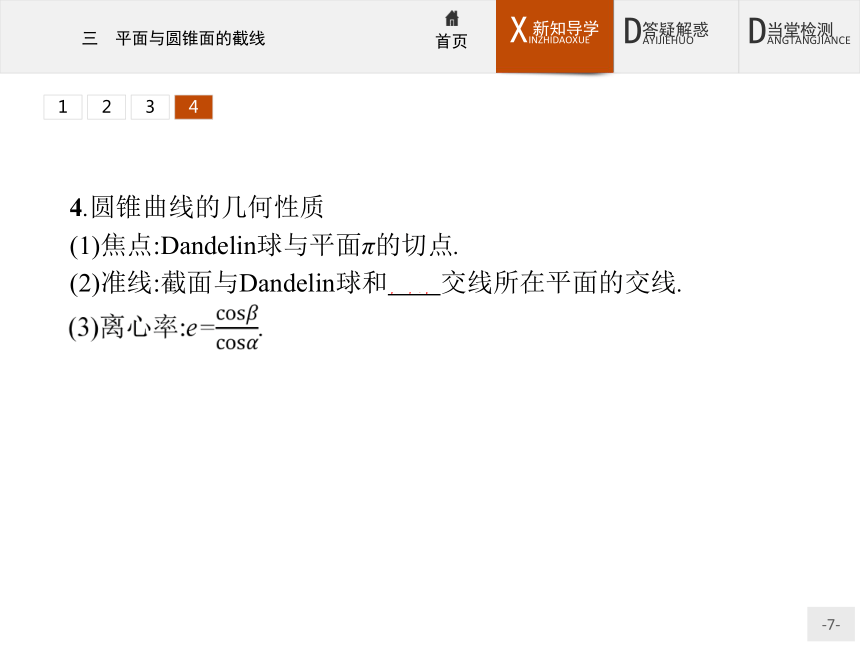
(1)焦点:Dandelin球与平面π的切点.
(2)准线:截面与Dandelin球和圆锥交线所在平面的交线.12341234做一做2 已知圆锥的轴截面为等边三角形,一个平面与圆锥轴的夹角为60°,则该平面与圆锥面的截线的离心率等于( )?1234思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)用一个不经过圆锥顶点的平面截圆锥面,截线只可能是椭圆、双曲线、抛物线. ( )
(2)在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别为F1,F2,则F1,F2即为平面π截圆锥所得双曲线的焦点. ( )
(3)所有圆锥曲线都有两个焦点和两条准线. ( )
(4)平面截圆锥面,所得圆锥曲线的离心率等于截面和圆锥的轴的交角的余弦与圆锥的母线和轴所成角的余弦之比. ( )
答案(1)× (2)√ (3)× (4)√探究一探究二思维辨析探究一平面截圆锥面截线形状的判断?
【例1】
在空间中,取直线l为轴,直线l'与l相交于O点,夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面.任取平面π,若它与轴l的交角为β,求证:β<α时,平面π与圆锥面的交线是双曲线(如图所示).分析利用Dandelin双球方法作答. 探究一探究二思维辨析解如图所示,当β<α时,平面π与圆锥的两部分相交.在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别是F1,F2,与圆锥两部分截得的圆分别为S1,S2.
在截口上任取一点P,连接PF1,PF2.过P和圆锥的顶点O作母线,分别与两个球相切于Q1,Q2,则PF1=PQ1,PF2=PQ2,所以|PF1-PF2|=|PQ1-PQ2|=Q1Q2.由于Q1Q2为两圆S1,S2所在平行平面之间的母线线段长,因此Q1Q2为定值.故由双曲线的定义知,平面与圆锥的交线是双曲线.探究一探究二思维辨析变式训练1 在【例1】中的情形下,说明当β=α时,平面π与圆锥面的截线是抛物线(如图所示).?探究一探究二思维辨析解如图所示,设平面π与圆锥内切球相切于点F1,球与圆锥的交线为S,过该交线的平面为π',π与π'相交于直线m.
在平面π与圆锥的截线上任取一点P,连接PF1,
过点P作PA⊥m,交m于点A,
过点P作π'的垂线,垂足为B.
连接AB,则AB⊥m,所以∠PAB是π与π'所成二面角的平面角,连接PO与S相交于Q1,连接BQ1,则∠BPQ1=α,∠APB=β.探究一探究二思维辨析探究一探究二思维辨析探究二平面截圆锥面截线的几何性质?
【例2】一平面截圆锥的截线为椭圆,椭圆的长轴长为8,长轴的两端点到顶点的距离分别为6和10,则椭圆的离心率为( )探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析审题不清致误
典例圆锥的顶角为50°,圆锥的截面与轴成30°角,则截线是( )
A.圆 B.椭圆
C.双曲线 D.抛物线
错解由于α=50°,β=30°,β<α,故所得截线是双曲线,故选C.
正解由于 ,β=30°,β>α,所得截线是椭圆,故选B.探究一探究二思维辨析探究一探究二思维辨析变式训练 圆锥的顶角为60°,截面与母线所成的角为60°,则截面所得的截线是( )?
A.圆 B.椭圆 C.双曲线 D.抛物线
解析该圆锥的轴截面如图所示,由题意知,截面与圆锥的轴垂直,故截线为圆.
答案A123451.已知AD是等边三角形ABC上的高,直线l与AD相交于点P,且与AD的夹角为β,当l与AB(或AB的延长线),AC都相交时,β的取值范围是( )
解析作出图形,由图形计算可得.
答案D123452.一圆锥面的母线和轴线成30°角,当用一与轴线成30°的不过顶点的平面去截圆锥面时,所截得的截线是( )
A.椭圆
B.双曲线
C.抛物线
D.两条相交直线
解析因为α=β=30°,
所以截线为抛物线.
答案C123453.已知圆锥母线与轴线夹角为60°,平面π与轴线夹角为45°,则平面π与圆锥交线的形状是 ,其离心率为 .?123454.用一个平面去截一个正圆锥,而且这个平面不通过圆锥的顶点,则截线会出现四种情况: .?
解析如图:
答案圆、抛物线、椭圆、双曲线123455.设圆锥的顶角(圆锥轴截面上两条母线的夹角)为120°,当圆锥的截面与轴成45°角时,求截得二次曲线的形状及离心率.
解由题意知α=60°,β=45°,满足β<α,这时截面截圆锥得到的交线
如下图,AD是等腰三角形ABC底边BC上的高,∠BAD=α,直线l与AD
(1)当β>α时,l与AB(或AB的延长线),AC都相交;
(2)当β=α时,l与AB不相交;
(3)当β<α时,l与BA的延长线、AC都相交.12342.定理2
在空间中,取直线l为轴,直线l'与l相交于O点,夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面.任取平面π,若它与轴l的交角为β(当π与l平行时,记β=0),则:
(1)若β>α,则平面π与圆锥的交线为椭圆;
(2)若β=α,则平面π与圆锥的交线为抛物线;
(3)若β<α,则平面π与圆锥的交线为双曲线.1234做一做1 已知圆锥的母线与轴的夹角为50°,一个平面与圆锥轴的夹角为40°,则该平面与圆锥面的截线为 ( )?
A.椭圆 B.圆 C.双曲线 D.抛物线
解析因为α=50°,β=40°,β<α,所以该平面与圆锥面的截线为双曲线.
答案C12343.圆锥曲线的结构特点
(1)椭圆上的点到两个定点(焦点)的距离之和为常数(长轴长2a);
(2)双曲线上的点到两个定点(焦点)的距离之差的绝对值为常数(实轴长2a);
(3)抛物线上的点到一个定点(焦点)和一条定直线的距离相等.12344.圆锥曲线的几何性质
(1)焦点:Dandelin球与平面π的切点.
(2)准线:截面与Dandelin球和圆锥交线所在平面的交线.12341234做一做2 已知圆锥的轴截面为等边三角形,一个平面与圆锥轴的夹角为60°,则该平面与圆锥面的截线的离心率等于( )?1234思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)用一个不经过圆锥顶点的平面截圆锥面,截线只可能是椭圆、双曲线、抛物线. ( )
(2)在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别为F1,F2,则F1,F2即为平面π截圆锥所得双曲线的焦点. ( )
(3)所有圆锥曲线都有两个焦点和两条准线. ( )
(4)平面截圆锥面,所得圆锥曲线的离心率等于截面和圆锥的轴的交角的余弦与圆锥的母线和轴所成角的余弦之比. ( )
答案(1)× (2)√ (3)× (4)√探究一探究二思维辨析探究一平面截圆锥面截线形状的判断?
【例1】
在空间中,取直线l为轴,直线l'与l相交于O点,夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面.任取平面π,若它与轴l的交角为β,求证:β<α时,平面π与圆锥面的交线是双曲线(如图所示).分析利用Dandelin双球方法作答. 探究一探究二思维辨析解如图所示,当β<α时,平面π与圆锥的两部分相交.在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别是F1,F2,与圆锥两部分截得的圆分别为S1,S2.
在截口上任取一点P,连接PF1,PF2.过P和圆锥的顶点O作母线,分别与两个球相切于Q1,Q2,则PF1=PQ1,PF2=PQ2,所以|PF1-PF2|=|PQ1-PQ2|=Q1Q2.由于Q1Q2为两圆S1,S2所在平行平面之间的母线线段长,因此Q1Q2为定值.故由双曲线的定义知,平面与圆锥的交线是双曲线.探究一探究二思维辨析变式训练1 在【例1】中的情形下,说明当β=α时,平面π与圆锥面的截线是抛物线(如图所示).?探究一探究二思维辨析解如图所示,设平面π与圆锥内切球相切于点F1,球与圆锥的交线为S,过该交线的平面为π',π与π'相交于直线m.
在平面π与圆锥的截线上任取一点P,连接PF1,
过点P作PA⊥m,交m于点A,
过点P作π'的垂线,垂足为B.
连接AB,则AB⊥m,所以∠PAB是π与π'所成二面角的平面角,连接PO与S相交于Q1,连接BQ1,则∠BPQ1=α,∠APB=β.探究一探究二思维辨析探究一探究二思维辨析探究二平面截圆锥面截线的几何性质?
【例2】一平面截圆锥的截线为椭圆,椭圆的长轴长为8,长轴的两端点到顶点的距离分别为6和10,则椭圆的离心率为( )探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析审题不清致误
典例圆锥的顶角为50°,圆锥的截面与轴成30°角,则截线是( )
A.圆 B.椭圆
C.双曲线 D.抛物线
错解由于α=50°,β=30°,β<α,故所得截线是双曲线,故选C.
正解由于 ,β=30°,β>α,所得截线是椭圆,故选B.探究一探究二思维辨析探究一探究二思维辨析变式训练 圆锥的顶角为60°,截面与母线所成的角为60°,则截面所得的截线是( )?
A.圆 B.椭圆 C.双曲线 D.抛物线
解析该圆锥的轴截面如图所示,由题意知,截面与圆锥的轴垂直,故截线为圆.
答案A123451.已知AD是等边三角形ABC上的高,直线l与AD相交于点P,且与AD的夹角为β,当l与AB(或AB的延长线),AC都相交时,β的取值范围是( )
解析作出图形,由图形计算可得.
答案D123452.一圆锥面的母线和轴线成30°角,当用一与轴线成30°的不过顶点的平面去截圆锥面时,所截得的截线是( )
A.椭圆
B.双曲线
C.抛物线
D.两条相交直线
解析因为α=β=30°,
所以截线为抛物线.
答案C123453.已知圆锥母线与轴线夹角为60°,平面π与轴线夹角为45°,则平面π与圆锥交线的形状是 ,其离心率为 .?123454.用一个平面去截一个正圆锥,而且这个平面不通过圆锥的顶点,则截线会出现四种情况: .?
解析如图:
答案圆、抛物线、椭圆、双曲线123455.设圆锥的顶角(圆锥轴截面上两条母线的夹角)为120°,当圆锥的截面与轴成45°角时,求截得二次曲线的形状及离心率.
解由题意知α=60°,β=45°,满足β<α,这时截面截圆锥得到的交线
