高中数学人教A版选修 4-5课件:3.3 排序不等式 :21张PPT
文档属性
| 名称 | 高中数学人教A版选修 4-5课件:3.3 排序不等式 :21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 00:00:00 | ||
图片预览








文档简介
课件21张PPT。三 排序不等式1.基本概念
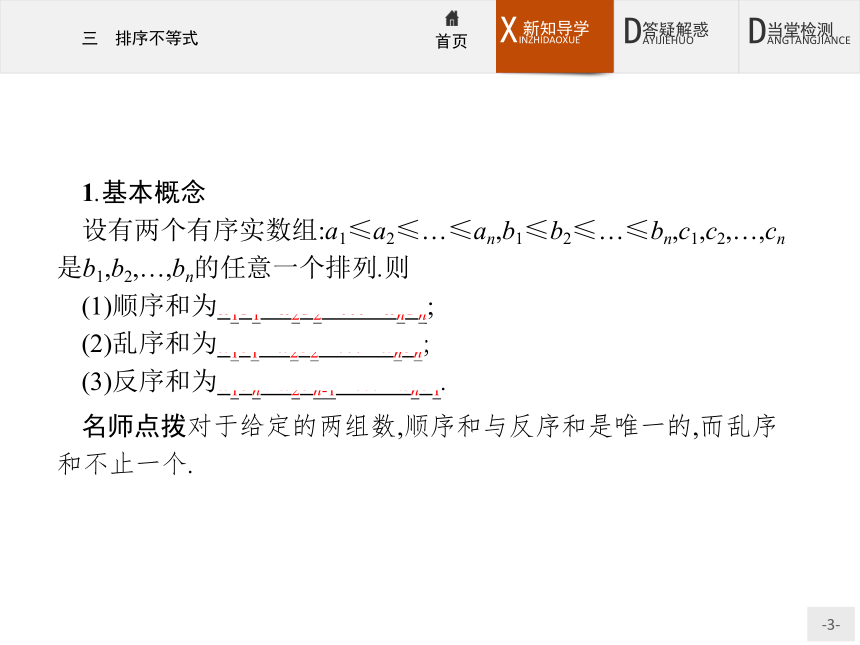
设有两个有序实数组:a1≤a2≤…≤an,b1≤b2≤…≤bn,c1,c2,…,cn是b1,b2,…,bn的任意一个排列.则
(1)顺序和为a1b1+a2b2+…+anbn;
(2)乱序和为a1c1+a2c2+…+ancn;
(3)反序和为a1bn+a2bn-1+…+anb1.名师点拨对于给定的两组数,顺序和与反序和是唯一的,而乱序和不止一个.做一做1 已知两组数:1,2,3和10,15,30,则顺序和等于 ,反序和等于 ,乱序和分别为 、 、 、 .?
解析:顺序和等于1×10+2×15+3×30=130;
反序和等于1×30+2×15+3×10=90;
乱序和分别为1×10+2×30+3×15=115,1×15+2×10+3×30=125,1×15+2×30+3×10=105,1×30+2×10+3×15=95.
答案:130 90 115 125 105 952.排序不等式(排序原理)
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则a1bn+a2bn-1+…+anb1≤a1c1+a2c2+…+ancn≤a1b1+a2b2+…+anbn,当且仅当a1=a2=…=an或b1=b2=…=bn时,反序和等于顺序和.名师点拨1.排序不等式(排序)是对不同的两个数组来研究不同的乘积和的问题,能构造的和按数组中的某种“搭配”的顺序被分为三种形式:顺序和、反序和、乱序和,对这三种不同的搭配形式只需注重是怎样的“次序”,两种较为简单的是“顺与反”,而乱序和则是不按“常规”的顺序.
2.排序不等式中取等号的条件是a1=a2=…=an或b1=b2=…=bn,对于我们解决某些问题非常关键,它是命题成立的一种条件,因此要牢记.做一做2 已知两组数1,2,3和25,30,45.若c1,c2,c3是25,30,45的一个排列,则c1+2c2+3c3的最大值是 ,最小值是 .?
解析:c1+2c2+3c3的最大值应该是顺序和1×25+2×30+3×45=220,最小值则为反序和1×45+2×30+3×25=180.
答案:220 180思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)对于给定的两组数,顺序和、反序和与乱序和都是唯一的. ( )
(2)对于任意给定的两组数,反序和不大于顺序和. ( )
(3)设a1,a2,a3是1,2,3的一个排序,则a1+2a2+3a3的最大值是14. ( )
(4)若a1,a2,a3,a4是1,2,3,4的一个排序,则 的最大值是4. ( )× √ √ × 探究一探究二利用排序不等式证明不等式?
【例1】 设a1,a2,…,an是1,2,…,n的一个排列,分析:构造数组,利用排序不等式证明. 探究一探究二反思感悟当所证不等式中涉及的变量已经给出大小关系时,可以根据待证不等式各部分的结构特点,构造数组,从而可以将待证不等式中的各部分视作是给定数组的顺序和、反序和或乱序和,从而借助排序不等式证得结论.探究一探究二变式训练1 设x,y,z为正数,探究一探究二【例2】 已知a,b,c>0,
分析:由于所要证的不等式中a,b,c的“地位”是对称的,因此可以先设出a,b,c的大小.探究一探究二反思感悟当所证不等式中涉及的变量没有给出大小关系,并且所证不等式与这些变量的大小关系无关时,通常可以先限定或假设出这些变量之间的大小顺序,再将待证不等式中的各部分视作是给定数组的顺序和、反序和或乱序和,从而借助排序不等式证得结论.探究一探究二探究一探究二利用排序不等式求最值?
【例3】 若a,b,c>0,
分析:利用排序不等式求解最小值关键是首先找出两组有序数组,然后根据反序和≤乱序和≤顺序和求解最小值.探究一探究二反思感悟利用排序不等式求最值的方法
利用排序不等式求最值时,先要对求解不等式及已知条件仔细分析,观察不等式的结构,明确两个数组的大小顺序,分清顺序和、乱序和及反序和.由于乱序和是不确定的,根据需要写出其中的一个即可.一般最值是顺序和或反序和.探究一探究二变式训练3 若a1,a2,a3>0,且a1+a2+a3=1, 1 2 3 4 51.已知两组数a1≤a2≤a3≤a4≤a5,b1≤b2≤b3≤b4≤b5,其中a1=2,a2=7,a3=8,a4=9,a5=12,b1=3,b2=4,b3=6,b4=10,b5=11,将bi(i=1,2,3,4,5)重新排列后记为c1,c2,c3,c4,c5,则a1c1+a2c2+a3c3+a4c4+a5c5的最大值与最小值分别为( )
A.132,6 B.304,212
C.22,6 D.21,36
解析:顺序和最大,所以最大值为a1b1+a2b2+a3b3+a4b4+a5b5=304;反序和最小,所以最小值为a1b5+a2b4+a3b3+a4b2+a5b1=212.
答案:B1 2 3 4 52.设a1,a2,…,an都是正数,b1,b2,…,bn是a1,a2,…,an的任意一个排列,则
的最小值为( )
A.1 B.n
C.n2 D.无法确定答案:B 1 2 3 4 53.某班学生要开联欢会,需要购买价格不同的礼品4件、5件及2件,现选择商店中单价为3元、2元和1元的礼品,则购买最少和最多花的钱数分别为( )
A.19元,24元 B.19元,20元
C.19元,25元 D.25元,27元
解析:由排序不等式可知,最少为2×3+4×2+5×1=19(元),最多为2×1+4×2+5×3=25(元).
答案:C1 2 3 4 54.设a≥b>0,则a3+b3与a2b+ab2的大小关系是 .?
解析:因为a≥b>0,所以a2≥b2>0,于是顺序和a·a2+b·b2=a3+b3,反序和为a2b+ab2,由排序不等式可得a3+b3≥a2b+ab2.
答案:a3+b3≥a2b+ab21 2 3 4 5
设有两个有序实数组:a1≤a2≤…≤an,b1≤b2≤…≤bn,c1,c2,…,cn是b1,b2,…,bn的任意一个排列.则
(1)顺序和为a1b1+a2b2+…+anbn;
(2)乱序和为a1c1+a2c2+…+ancn;
(3)反序和为a1bn+a2bn-1+…+anb1.名师点拨对于给定的两组数,顺序和与反序和是唯一的,而乱序和不止一个.做一做1 已知两组数:1,2,3和10,15,30,则顺序和等于 ,反序和等于 ,乱序和分别为 、 、 、 .?
解析:顺序和等于1×10+2×15+3×30=130;
反序和等于1×30+2×15+3×10=90;
乱序和分别为1×10+2×30+3×15=115,1×15+2×10+3×30=125,1×15+2×30+3×10=105,1×30+2×10+3×15=95.
答案:130 90 115 125 105 952.排序不等式(排序原理)
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则a1bn+a2bn-1+…+anb1≤a1c1+a2c2+…+ancn≤a1b1+a2b2+…+anbn,当且仅当a1=a2=…=an或b1=b2=…=bn时,反序和等于顺序和.名师点拨1.排序不等式(排序)是对不同的两个数组来研究不同的乘积和的问题,能构造的和按数组中的某种“搭配”的顺序被分为三种形式:顺序和、反序和、乱序和,对这三种不同的搭配形式只需注重是怎样的“次序”,两种较为简单的是“顺与反”,而乱序和则是不按“常规”的顺序.
2.排序不等式中取等号的条件是a1=a2=…=an或b1=b2=…=bn,对于我们解决某些问题非常关键,它是命题成立的一种条件,因此要牢记.做一做2 已知两组数1,2,3和25,30,45.若c1,c2,c3是25,30,45的一个排列,则c1+2c2+3c3的最大值是 ,最小值是 .?
解析:c1+2c2+3c3的最大值应该是顺序和1×25+2×30+3×45=220,最小值则为反序和1×45+2×30+3×25=180.
答案:220 180思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)对于给定的两组数,顺序和、反序和与乱序和都是唯一的. ( )
(2)对于任意给定的两组数,反序和不大于顺序和. ( )
(3)设a1,a2,a3是1,2,3的一个排序,则a1+2a2+3a3的最大值是14. ( )
(4)若a1,a2,a3,a4是1,2,3,4的一个排序,则 的最大值是4. ( )× √ √ × 探究一探究二利用排序不等式证明不等式?
【例1】 设a1,a2,…,an是1,2,…,n的一个排列,分析:构造数组,利用排序不等式证明. 探究一探究二反思感悟当所证不等式中涉及的变量已经给出大小关系时,可以根据待证不等式各部分的结构特点,构造数组,从而可以将待证不等式中的各部分视作是给定数组的顺序和、反序和或乱序和,从而借助排序不等式证得结论.探究一探究二变式训练1 设x,y,z为正数,探究一探究二【例2】 已知a,b,c>0,
分析:由于所要证的不等式中a,b,c的“地位”是对称的,因此可以先设出a,b,c的大小.探究一探究二反思感悟当所证不等式中涉及的变量没有给出大小关系,并且所证不等式与这些变量的大小关系无关时,通常可以先限定或假设出这些变量之间的大小顺序,再将待证不等式中的各部分视作是给定数组的顺序和、反序和或乱序和,从而借助排序不等式证得结论.探究一探究二探究一探究二利用排序不等式求最值?
【例3】 若a,b,c>0,
分析:利用排序不等式求解最小值关键是首先找出两组有序数组,然后根据反序和≤乱序和≤顺序和求解最小值.探究一探究二反思感悟利用排序不等式求最值的方法
利用排序不等式求最值时,先要对求解不等式及已知条件仔细分析,观察不等式的结构,明确两个数组的大小顺序,分清顺序和、乱序和及反序和.由于乱序和是不确定的,根据需要写出其中的一个即可.一般最值是顺序和或反序和.探究一探究二变式训练3 若a1,a2,a3>0,且a1+a2+a3=1, 1 2 3 4 51.已知两组数a1≤a2≤a3≤a4≤a5,b1≤b2≤b3≤b4≤b5,其中a1=2,a2=7,a3=8,a4=9,a5=12,b1=3,b2=4,b3=6,b4=10,b5=11,将bi(i=1,2,3,4,5)重新排列后记为c1,c2,c3,c4,c5,则a1c1+a2c2+a3c3+a4c4+a5c5的最大值与最小值分别为( )
A.132,6 B.304,212
C.22,6 D.21,36
解析:顺序和最大,所以最大值为a1b1+a2b2+a3b3+a4b4+a5b5=304;反序和最小,所以最小值为a1b5+a2b4+a3b3+a4b2+a5b1=212.
答案:B1 2 3 4 52.设a1,a2,…,an都是正数,b1,b2,…,bn是a1,a2,…,an的任意一个排列,则
的最小值为( )
A.1 B.n
C.n2 D.无法确定答案:B 1 2 3 4 53.某班学生要开联欢会,需要购买价格不同的礼品4件、5件及2件,现选择商店中单价为3元、2元和1元的礼品,则购买最少和最多花的钱数分别为( )
A.19元,24元 B.19元,20元
C.19元,25元 D.25元,27元
解析:由排序不等式可知,最少为2×3+4×2+5×1=19(元),最多为2×1+4×2+5×3=25(元).
答案:C1 2 3 4 54.设a≥b>0,则a3+b3与a2b+ab2的大小关系是 .?
解析:因为a≥b>0,所以a2≥b2>0,于是顺序和a·a2+b·b2=a3+b3,反序和为a2b+ab2,由排序不等式可得a3+b3≥a2b+ab2.
答案:a3+b3≥a2b+ab21 2 3 4 5
