冀教版 七年级上册数学第二章几何图形的初步认识2.7 角的和与差同步检测(解析版)
文档属性
| 名称 | 冀教版 七年级上册数学第二章几何图形的初步认识2.7 角的和与差同步检测(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 335.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-07 00:00:00 | ||
图片预览



文档简介
2.7 角的和与差
基础闯关全练
知识点一 角的和与差
1.如图2-7-1所示,下列式子中错误的是 ( )
A.∠AOC= ∠AOB+∠BOC
B.∠AOC= ∠AOD-∠COD
C.∠AOC= ∠AOB+∠BOD-∠BOC
D.∠AOC= ∠AOD-∠BOD+∠BOC
2.如图2-7-2,∠AOB=∠COD= 90°,∠BOC= 32°,则∠AOD等于 ( )
A.58° B.158° C.148° D.138°
3.把一副三角板按照图2-7-3所示的位置拼在一起,不重叠也没有缝隙,则∠ABC的度数为 .
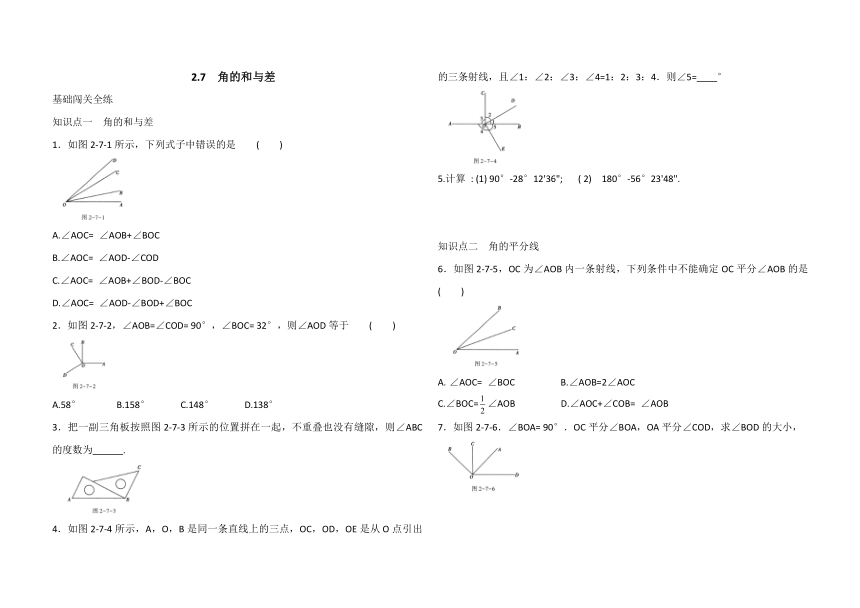
4.如图2-7-4所示,A,O,B是同一条直线上的三点,OC,OD,OE是从O点引出的三条射线,且∠1:∠2:∠3:∠4=1:2:3:4.则∠5= °
5.计算 : (1) 90°-28°12'36"; ( 2) 180°-56°23'48".
知识点二 角的平分线
6.如图2-7-5,OC为∠AOB内一条射线,下列条件中不能确定OC平分∠AOB的是 ( )
∠AOC= ∠BOC B.∠AOB=2∠AOC
C.∠BOC=∠AOB D.∠AOC+∠COB= ∠AOB
7.如图2-7-6.∠BOA= 90°.OC平分∠BOA,OA平分∠COD,求∠BOD的大小,
知识点三 互为余角、互为补角的概念及性质
8.一个角的余角是54°26'.则这个角的补角是 .
9.如图2-7-7所示,将一副三角板的直角顶点O重合,证明∠AOD= ∠COB,并求∠AOC+∠ BOD的度数.
能力提升全练
1.如果∠α和∠β互补,且∠α>∠β,那么下列表示∠β的余角的式子中,正确的有 ( )
①90°-∠β;②∠α - 90°;③(∠α+∠β);④(∠α-∠β).
A.4个 B.3个 C.2个 D.1个
2.如图2-7-8,OM是∠AOB的平分线,OP是∠MOB内的一条射线,已知∠AOP比∠BOP大30°,则∠MOP= .
3.如图2-7-9,∠AOB=∠DOC= 90°,OE平分∠AOD,反向延长射线OE至F.
(1) ∠AOD和∠BOC是否互补?说明理由:
(2)射线OF是∠BOC的平分线吗?说明理由.
4.如图2-7-10.已知∠AOB= ∠COD=90°,∠BOC= 34°.
(1)判断∠BOC与∠AOD之间的数量关系,并说明理由;
(2)若OE平分∠AOC,求∠EOC的余角的度数.
三年模拟全练
一、选择题
1.已知∠α与∠β互补,∠α=5∠β,则∠α等于 ( )
A.150° B.120° C.90° D.60°
2.如图2 -7 - 11,O是直线AB上一点,OD平分∠AOC,∠DOE=90°,则以下结论正确的个数是 ( )
①∠AOD与∠BOE互为余角;②∠AOD=∠COE:
③∠BOE=∠COE;④∠DOC与∠DOB互补.
A.1 B.2 C.3 D.4
二、解答题
3.如图2-7 -12,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOC.
(1)请写出∠EOC的余角;
(2)若∠BOC= 40°,求∠EOF的度数.
4.如图2-7-13,直线AB,CD相交于点O,OF平分∠AOE,∠DOF= 90°,垂足为O.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE= 120°,求∠BOD的度数.
五年中考全练
一、选择题
1.(2018广西梧州中考,4)已知∠A= 55°,则它的余角是 ( )
A.25° B.35° C.45° D.55°
2.(2018甘肃陇南中考,3)若一个角为65°,则它的补角的度数为 ( )
A.25° B.35° C.115° D.125°
二、填空题
3.(2018由东日照中考,13)一个角是70°39',则它的余角的度数是 .
核心素养全练
如图2 -7 - 14,直线AB上有一点O,∠DOB= 90°,∠EOC= 90°.
(1)如果∠DOE= 50°,则∠AOC的度数为 .
(2)直接写出图中相等的锐角,如果∠DOE≠50°,它们还会相等吗?
(3)若∠DOE变大,则∠AOC会如何变化?(不必说明理由)
答案
基础闯关全练
C
解析:易得A,B,D中等式成立,C中,∠AOC= ∠AOB+∠BOD-∠COD.故选C.
C
解析:因为∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°, ∠AOB=∠COD=90°,∠BOC,=32°,所以∠AOD=360°-90°-32°-90°=148°.
3.答案 120°
解析 ∠ABC= 30°+90°= 120°.
4.答案60
解析由A,O,B是同一条直线上的三点,得∠AOB=180°,又由∠1:∠2:∠3=1:2:3,可知∠1= 30°, ∠2= 60°, ∠3=90°,又∠1:∠2:∠3:∠4=1:2:3:4.所以∠4= 120°,所以∠5 =180°-120°= 60°.
5.解析(1)原式=89°59'60"- 28°12'36"=61°47 '24".
(2)原式=179°59'60"- 56°23 '48"= 123°36'12".
6.D
解析:A.∠AOC= ∠BOC能确定OC平分∠AOB,故此选项不合题意;B.∠AOB=2∠AOC能确定OC平分∠AOB,敞此选项不合题意;C.∠BOC=∠AOB,能确定OC平分∠AOB,故此选项不合题意;D.∠AOC+ ∠COB= ∠AOB不能确定OC平分∠AOB,故此选项符合题意.故选D.
7.解析∵∠BOA=90°,OC平分∠BOA.∠COA= 45°,
又∵OA平分∠COD,∴∠AOD= ∠COA=45°,
∴∠BOD= ∠BOA+∠AOD= 90°+45°=135°.
8.答案 144°26'
解析∵一个角的余角是54°26',∴这个角为90°-54°26'=35°34'.∴这个角的补角为180°-35°34'= 144°26'.
9.解析①证明:∵∠AOB= ∠DOC=90°,
∴∠AOB-∠DOB= ∠DOC-∠DOB.
∴ ∠ AOD =∠ BOC.
(2)∵∠AOB = ∠ DOC = 900 , ∴∠AOC+ ∠BOD=∠AOB+ ∠ BOC+ ∠ BOD = ∠AOB+ ∠DOC = 90°+90° = 180°.
能力提升全练
B
解析:因为90°-∠β+∠β=90°,所以①正确;因为∠α- 90°+∠β= ∠α+∠β-90°= 180°-90°= 90°,所以②正确;因为(∠α+∠β)+∠β= x 180°+∠β= 90°+∠β≠90°,所以③错误;因为(∠α-∠β)+∠β=(∠α+∠β)=×180°= 90°,所以④
正确,故选B.
2.答案15°
解析 因为OM是∠AOB的平分线,所以∠AOM= ∠BOM,所以∠AOP- ∠POM=∠BOP+ ∠POM, 所以∠AOP- ∠BOP=2∠POM.因为∠AOP比∠BOP大30°,所以2∠POM= 30°,所以MOP= 15°.
3.解析(1)互补.理由如下:
因为∠AOD+ ∠BOC= 360° -∠ AOB - ∠DOC= 360° - 90° - 90°= 180°,
所以∠ AOD和∠BOC互补.
(2)射线OF是∠BOC的平分线,理由如下:
因为OE平分∠ AOD,
所以∠AOE=∠DOE,
因为∠COF=180°-∠DOC-∠DOE=90°-∠DOE,
∠ BOF= 180°-∠AOB-∠AOE= 90°- ∠AOE.
所以∠ COF=∠BOF,即射线OF是∠BOC的平分线.
4.解析 (1) ∠BOC+∠AOD= 180°,理由如下:
因为∠ AOB= ∠COD= 90°, ∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°,
所以∠ BOC+ ∠AOD= 360°-∠AOB-∠ COD= 180°.
(2)因为∠AOB=90°,∠BOC=34°,
所以∠ AOC= ∠AOB+∠BOC=124°,
因为OE平分∠AOC,
所以∠EOC= ∠AOE=∠AOC=62°.
所以∠EOC的余角的度数为90°-∠EOC=28°,
三年模拟全练
一、选择题
1.A
解析: ∵∠α与∠β互补.∴∠α+ ∠β= 180°,∵∠α=5∠β,
∴5 ∠β+∠β= 180°,∴∠β= 30°,∴∠α= 150°,故选A.
C
解析: (1)∵∠ DOF,= 90°,∴∠AOD+∠ BOE= 90°,∴∠AOD与∠BOE互为余角,故①正确:②∵DD平分∠ AOC,∴∠AOD=∠COD,∵∠DOC+∠COE= 90°,∴∠AOD+ ∠COE= 90°.故② 错误;③∵ OD平分∠AOC.∴∠AOD=∠COD,∵∠DOC+ ∠COE=90°,∠AOD+∠BOE=90°,∴∠CDE=∠BOE,故③正 确;④∵OD平分∠AOC,∴∠AOD=∠COD,∵∠AOD+∠DOB = 180°,∴∠DOC+∠ DOB= 180°,故④正确,故选C.
二、解答题
3.解析 (1) ∠EOC的余角有∠BOC、∠AOD.
(2)∵∠ BOC= 40°,∴∠AOC= 180°-40°= 140°.
∵OF平分∠AOC.∠FOA=×140°=70°,
∵EO⊥AB,∴∠EOA=90°,
∴∠EOF=∠EOA-∠FOA=90°-70°=20°.
4.解析 (1)∵直线AB,CD相交于点O
∴∠AOC,∠BOD与∠AOD互补,
∵OF平分∠AOE,∴∠AOF=∠EOF.
∵∠DOF= 90°.∴∠ COF=∠ DOF= 90°.∴∠DOE=∠AOC.
∴∠DOE也是∠AOD的补角.
∴与∠ AOD互补的角有∠AOC,∠BOD,∠DOE.
(2)∵OF分∠AOE,∴∠AOF=∠AOE=60°,
∵∠ DOF=90°,
∴∠BOD= 180°-∠ AOF -∠DOF= 180°-90°-60°=30°.
五年中考全练
一、选择题
1.B
解析:∵∠A= 55°.∴它的余角的度数是90°-∠A=90°-55°=35°,故选B.
2.C
解析:根据互为补角的两个角的度数的和等于180°,得180°-65°= 115°.
二、填空题
3.答案19°21'
解析它的余角的度数是90°-70°39'= 19°21'.
核心素养全练
解析 (1)∵∠DOB=90°,∴∠AOD=90°,
∵∠ DOE= 50°,∠EOC= 90°,∴∠DOC= 40°,
∴∠AOC= 90°+40°= 130°
故答案为130°.
(2) ∠AOE= ∠DOC,∠EOD=∠ COB,如果∠DOE ≠50°,它们
还会相等.理由:
∵∠AOD= 90°,∠AOF+∠EOD= 90°.
∵∠EOC= 90°.∴∠EOD+∠DOC= 90°,∴∠AOE=∠DOC,
∵∠DOB= 90°,∴∠DOC+∠COB= 90°,∴∠EOD= ∠COB.
(3)若∠DOE变大,则∠AOC变小.
∵∠EOC=90°,∴∠DOE+∠DOC=90°.
∵∠ DOE变大.∴∠DOC变小,
∵∠ AOC= ∠AOD+∠DOC=90°+∠DOC.∴AOC变小.
基础闯关全练
知识点一 角的和与差
1.如图2-7-1所示,下列式子中错误的是 ( )
A.∠AOC= ∠AOB+∠BOC
B.∠AOC= ∠AOD-∠COD
C.∠AOC= ∠AOB+∠BOD-∠BOC
D.∠AOC= ∠AOD-∠BOD+∠BOC
2.如图2-7-2,∠AOB=∠COD= 90°,∠BOC= 32°,则∠AOD等于 ( )
A.58° B.158° C.148° D.138°
3.把一副三角板按照图2-7-3所示的位置拼在一起,不重叠也没有缝隙,则∠ABC的度数为 .
4.如图2-7-4所示,A,O,B是同一条直线上的三点,OC,OD,OE是从O点引出的三条射线,且∠1:∠2:∠3:∠4=1:2:3:4.则∠5= °
5.计算 : (1) 90°-28°12'36"; ( 2) 180°-56°23'48".
知识点二 角的平分线
6.如图2-7-5,OC为∠AOB内一条射线,下列条件中不能确定OC平分∠AOB的是 ( )
∠AOC= ∠BOC B.∠AOB=2∠AOC
C.∠BOC=∠AOB D.∠AOC+∠COB= ∠AOB
7.如图2-7-6.∠BOA= 90°.OC平分∠BOA,OA平分∠COD,求∠BOD的大小,
知识点三 互为余角、互为补角的概念及性质
8.一个角的余角是54°26'.则这个角的补角是 .
9.如图2-7-7所示,将一副三角板的直角顶点O重合,证明∠AOD= ∠COB,并求∠AOC+∠ BOD的度数.
能力提升全练
1.如果∠α和∠β互补,且∠α>∠β,那么下列表示∠β的余角的式子中,正确的有 ( )
①90°-∠β;②∠α - 90°;③(∠α+∠β);④(∠α-∠β).
A.4个 B.3个 C.2个 D.1个
2.如图2-7-8,OM是∠AOB的平分线,OP是∠MOB内的一条射线,已知∠AOP比∠BOP大30°,则∠MOP= .
3.如图2-7-9,∠AOB=∠DOC= 90°,OE平分∠AOD,反向延长射线OE至F.
(1) ∠AOD和∠BOC是否互补?说明理由:
(2)射线OF是∠BOC的平分线吗?说明理由.
4.如图2-7-10.已知∠AOB= ∠COD=90°,∠BOC= 34°.
(1)判断∠BOC与∠AOD之间的数量关系,并说明理由;
(2)若OE平分∠AOC,求∠EOC的余角的度数.
三年模拟全练
一、选择题
1.已知∠α与∠β互补,∠α=5∠β,则∠α等于 ( )
A.150° B.120° C.90° D.60°
2.如图2 -7 - 11,O是直线AB上一点,OD平分∠AOC,∠DOE=90°,则以下结论正确的个数是 ( )
①∠AOD与∠BOE互为余角;②∠AOD=∠COE:
③∠BOE=∠COE;④∠DOC与∠DOB互补.
A.1 B.2 C.3 D.4
二、解答题
3.如图2-7 -12,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOC.
(1)请写出∠EOC的余角;
(2)若∠BOC= 40°,求∠EOF的度数.
4.如图2-7-13,直线AB,CD相交于点O,OF平分∠AOE,∠DOF= 90°,垂足为O.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE= 120°,求∠BOD的度数.
五年中考全练
一、选择题
1.(2018广西梧州中考,4)已知∠A= 55°,则它的余角是 ( )
A.25° B.35° C.45° D.55°
2.(2018甘肃陇南中考,3)若一个角为65°,则它的补角的度数为 ( )
A.25° B.35° C.115° D.125°
二、填空题
3.(2018由东日照中考,13)一个角是70°39',则它的余角的度数是 .
核心素养全练
如图2 -7 - 14,直线AB上有一点O,∠DOB= 90°,∠EOC= 90°.
(1)如果∠DOE= 50°,则∠AOC的度数为 .
(2)直接写出图中相等的锐角,如果∠DOE≠50°,它们还会相等吗?
(3)若∠DOE变大,则∠AOC会如何变化?(不必说明理由)
答案
基础闯关全练
C
解析:易得A,B,D中等式成立,C中,∠AOC= ∠AOB+∠BOD-∠COD.故选C.
C
解析:因为∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°, ∠AOB=∠COD=90°,∠BOC,=32°,所以∠AOD=360°-90°-32°-90°=148°.
3.答案 120°
解析 ∠ABC= 30°+90°= 120°.
4.答案60
解析由A,O,B是同一条直线上的三点,得∠AOB=180°,又由∠1:∠2:∠3=1:2:3,可知∠1= 30°, ∠2= 60°, ∠3=90°,又∠1:∠2:∠3:∠4=1:2:3:4.所以∠4= 120°,所以∠5 =180°-120°= 60°.
5.解析(1)原式=89°59'60"- 28°12'36"=61°47 '24".
(2)原式=179°59'60"- 56°23 '48"= 123°36'12".
6.D
解析:A.∠AOC= ∠BOC能确定OC平分∠AOB,故此选项不合题意;B.∠AOB=2∠AOC能确定OC平分∠AOB,敞此选项不合题意;C.∠BOC=∠AOB,能确定OC平分∠AOB,故此选项不合题意;D.∠AOC+ ∠COB= ∠AOB不能确定OC平分∠AOB,故此选项符合题意.故选D.
7.解析∵∠BOA=90°,OC平分∠BOA.∠COA= 45°,
又∵OA平分∠COD,∴∠AOD= ∠COA=45°,
∴∠BOD= ∠BOA+∠AOD= 90°+45°=135°.
8.答案 144°26'
解析∵一个角的余角是54°26',∴这个角为90°-54°26'=35°34'.∴这个角的补角为180°-35°34'= 144°26'.
9.解析①证明:∵∠AOB= ∠DOC=90°,
∴∠AOB-∠DOB= ∠DOC-∠DOB.
∴ ∠ AOD =∠ BOC.
(2)∵∠AOB = ∠ DOC = 900 , ∴∠AOC+ ∠BOD=∠AOB+ ∠ BOC+ ∠ BOD = ∠AOB+ ∠DOC = 90°+90° = 180°.
能力提升全练
B
解析:因为90°-∠β+∠β=90°,所以①正确;因为∠α- 90°+∠β= ∠α+∠β-90°= 180°-90°= 90°,所以②正确;因为(∠α+∠β)+∠β= x 180°+∠β= 90°+∠β≠90°,所以③错误;因为(∠α-∠β)+∠β=(∠α+∠β)=×180°= 90°,所以④
正确,故选B.
2.答案15°
解析 因为OM是∠AOB的平分线,所以∠AOM= ∠BOM,所以∠AOP- ∠POM=∠BOP+ ∠POM, 所以∠AOP- ∠BOP=2∠POM.因为∠AOP比∠BOP大30°,所以2∠POM= 30°,所以MOP= 15°.
3.解析(1)互补.理由如下:
因为∠AOD+ ∠BOC= 360° -∠ AOB - ∠DOC= 360° - 90° - 90°= 180°,
所以∠ AOD和∠BOC互补.
(2)射线OF是∠BOC的平分线,理由如下:
因为OE平分∠ AOD,
所以∠AOE=∠DOE,
因为∠COF=180°-∠DOC-∠DOE=90°-∠DOE,
∠ BOF= 180°-∠AOB-∠AOE= 90°- ∠AOE.
所以∠ COF=∠BOF,即射线OF是∠BOC的平分线.
4.解析 (1) ∠BOC+∠AOD= 180°,理由如下:
因为∠ AOB= ∠COD= 90°, ∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°,
所以∠ BOC+ ∠AOD= 360°-∠AOB-∠ COD= 180°.
(2)因为∠AOB=90°,∠BOC=34°,
所以∠ AOC= ∠AOB+∠BOC=124°,
因为OE平分∠AOC,
所以∠EOC= ∠AOE=∠AOC=62°.
所以∠EOC的余角的度数为90°-∠EOC=28°,
三年模拟全练
一、选择题
1.A
解析: ∵∠α与∠β互补.∴∠α+ ∠β= 180°,∵∠α=5∠β,
∴5 ∠β+∠β= 180°,∴∠β= 30°,∴∠α= 150°,故选A.
C
解析: (1)∵∠ DOF,= 90°,∴∠AOD+∠ BOE= 90°,∴∠AOD与∠BOE互为余角,故①正确:②∵DD平分∠ AOC,∴∠AOD=∠COD,∵∠DOC+∠COE= 90°,∴∠AOD+ ∠COE= 90°.故② 错误;③∵ OD平分∠AOC.∴∠AOD=∠COD,∵∠DOC+ ∠COE=90°,∠AOD+∠BOE=90°,∴∠CDE=∠BOE,故③正 确;④∵OD平分∠AOC,∴∠AOD=∠COD,∵∠AOD+∠DOB = 180°,∴∠DOC+∠ DOB= 180°,故④正确,故选C.
二、解答题
3.解析 (1) ∠EOC的余角有∠BOC、∠AOD.
(2)∵∠ BOC= 40°,∴∠AOC= 180°-40°= 140°.
∵OF平分∠AOC.∠FOA=×140°=70°,
∵EO⊥AB,∴∠EOA=90°,
∴∠EOF=∠EOA-∠FOA=90°-70°=20°.
4.解析 (1)∵直线AB,CD相交于点O
∴∠AOC,∠BOD与∠AOD互补,
∵OF平分∠AOE,∴∠AOF=∠EOF.
∵∠DOF= 90°.∴∠ COF=∠ DOF= 90°.∴∠DOE=∠AOC.
∴∠DOE也是∠AOD的补角.
∴与∠ AOD互补的角有∠AOC,∠BOD,∠DOE.
(2)∵OF分∠AOE,∴∠AOF=∠AOE=60°,
∵∠ DOF=90°,
∴∠BOD= 180°-∠ AOF -∠DOF= 180°-90°-60°=30°.
五年中考全练
一、选择题
1.B
解析:∵∠A= 55°.∴它的余角的度数是90°-∠A=90°-55°=35°,故选B.
2.C
解析:根据互为补角的两个角的度数的和等于180°,得180°-65°= 115°.
二、填空题
3.答案19°21'
解析它的余角的度数是90°-70°39'= 19°21'.
核心素养全练
解析 (1)∵∠DOB=90°,∴∠AOD=90°,
∵∠ DOE= 50°,∠EOC= 90°,∴∠DOC= 40°,
∴∠AOC= 90°+40°= 130°
故答案为130°.
(2) ∠AOE= ∠DOC,∠EOD=∠ COB,如果∠DOE ≠50°,它们
还会相等.理由:
∵∠AOD= 90°,∠AOF+∠EOD= 90°.
∵∠EOC= 90°.∴∠EOD+∠DOC= 90°,∴∠AOE=∠DOC,
∵∠DOB= 90°,∴∠DOC+∠COB= 90°,∴∠EOD= ∠COB.
(3)若∠DOE变大,则∠AOC变小.
∵∠EOC=90°,∴∠DOE+∠DOC=90°.
∵∠ DOE变大.∴∠DOC变小,
∵∠ AOC= ∠AOD+∠DOC=90°+∠DOC.∴AOC变小.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
