4.1.1 立体图形与平面图形 同步练习(解析版)
文档属性
| 名称 | 4.1.1 立体图形与平面图形 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-08 00:00:00 | ||
图片预览


文档简介
初中数学人教版七年级上学期 第四章 4.1.1 立体图形与平面图形
一、基础巩固
1.长方形剪去一个角后所得的图形一定不是(? )
A.?五边形?????????????????????????????????B.?梯形?????????????????????????????????C.?长方形?????????????????????????????????D.?三角形
2.图中的几何体有(?? )条棱.
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
3.观察下列实物模型,其形状是圆柱体的是(?? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.下列图形属于圆锥的是(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
5.下面几何图形是平面图形的是(???? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
6.写出下图中各个几何体的名称,并按锥体和柱体把它们分类.
二、强化提升
7.某正方体的平面展开图如图所示,则原正方体中与“春”字所在的面相对的面上的字是(??? )
A.?青?????????????????????????????????????????B.?来?????????????????????????????????????????C.?斗?????????????????????????????????????????D.?奋
8.下列哪个图形是正方体的展开图( ??)
A.??????????????B.??????????????C.??????????????D.?
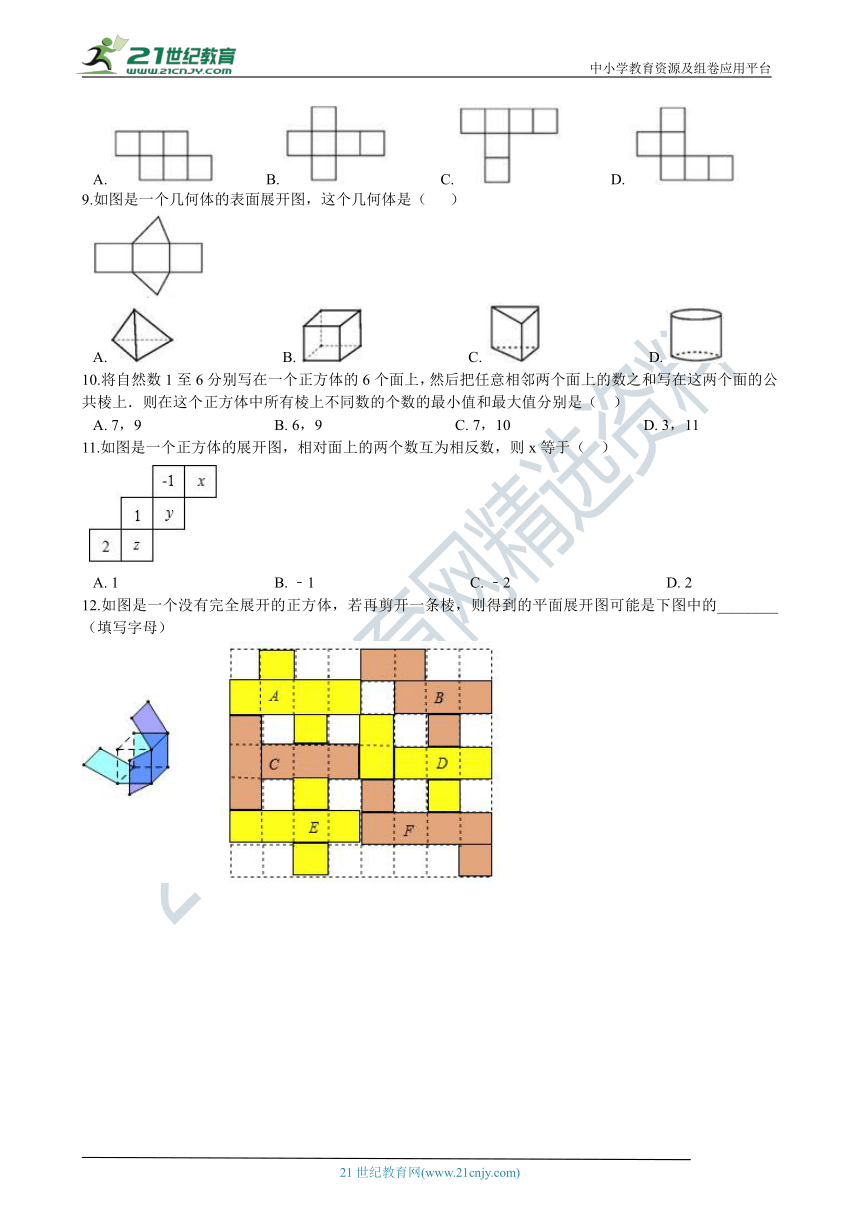
9.如图是一个几何体的表面展开图,这个几何体是(???? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
10.将自然数1至6分别写在一个正方体的6个面上,然后把任意相邻两个面上的数之和写在这两个面的公共棱上.则在这个正方体中所有棱上不同数的个数的最小值和最大值分别是(?? )
A.?7,9???????????????????????????????????B.?6,9???????????????????????????????????C.?7,10???????????????????????????????????D.?3,11
11.如图是一个正方体的展开图,相对面上的两个数互为相反数,则x等于(?? )
A.?1?????????????????????????????????????????B.?﹣1?????????????????????????????????????????C.?﹣2?????????????????????????????????????????D.?2
12.如图是一个没有完全展开的正方体,若再剪开一条棱,则得到的平面展开图可能是下图中的________(填写字母)21世纪教育网版权所有
答案解析部分
一、基础巩固
1. C
解:如图 当截线为经过正方形对角2个顶点的直线时,剩余图形为三角形(如图1); 当截线如图2所示,剩余图形是梯形(如图2); 当截线为只经过正方形一组邻边的一条直线时,剩余图形是五边形(如图3). 故不可能是长方形。 故答案为:C 21教育网
【分析】分情况讨论:当截线为经过正方形对角2个顶点的直线时如图1;当截线如图2所示;当截线为只经过正方形一组邻边的一条直线时,如图3,观察图形即可得出答案。21cnjy.com
2. D
解:此几何体有6条棱,
故答案为:D. 【分析】由图即可找出几何体的棱的数量。
3. D
解:圆柱的上下底面都是圆,所以正确的是D。 故答案为:D。 【分析】根据立体图形的特点及概念即可一一判断得出答案。21·cn·jy·com
4. C
A、此立体图形是四棱锥,不符合题意;
B、此立体图形是圆柱,不符合题意;
C、此立体图形是圆锥,符合题意;
D、此立体图形是直三棱柱,不符合题意;
故答案为:C. 【分析】根据圆锥、圆柱、棱柱、棱锥的特点分别分析即可求解.
5. A
解:由平面图形和立体图形的定义可知:A是平面图形,B、C、D是立体图形,
故答案为:A. 【分析】根据平面图形和立体图形的定义可求解.
6. 解:①圆柱②圆锥③四棱锥④五棱柱⑤三棱锥⑥四棱柱(或长方体)锥体有:②③⑤柱体有:①④⑥
【分析】柱体包括圆柱与棱柱,椎体包括圆锥和棱锥。棱柱:两底面是对应边平行的全等多边形,侧面,对角面都是平行四边形,侧棱平行且相等。圆柱:两个大小相同、互相平行的圆形底面,以及一个侧曲面。棱锥:侧面,对角面都是三角形。圆锥:有个圆形底面,侧面展开图是扇形。
二、强化提升
7. D
解:“ ”字型对面,可知春字对应的面上的字是奋;
故答案为:D.
【分析】根据正方体展开图的“Z”字型找对面的方法,就可得到答案。
8. B
解:根据正方形展开图的特征,只有选项B是正方体的展开图.
故答案为:B。 【分析】根据正方体展开图的11种特征,B选项属于中正方体展开图的“1-3-2”型,只有B符合.
9. C
解:由平面图形的折叠及三棱柱的展开图的特征可知,这个几何体是三棱柱.
故答案为:C. 【分析】由平面图形的折叠以及四个选项中的立体图形的展开图的特征即可作出判断。
10. A
证明:①根据题意,相邻两面上的数相加,正方体每个面都有4个相邻面,
所以:每个面的数字都是加4遍; 1、2、3、4、5、6这6个数的和为21;
所以:不论数字怎么摆放,12条棱12个数字的和恒等于:4×21=84
这6个数任取2个相加,只有9个不重复的数字:3,4,5,6,7,8,9,10,11
所以:根据“抽屉原理”,12条棱的数字至少重复3个.
即:棱上不同和数的个数最多9个! ②9个和数3,4,5,6,7,8,9,10,11分解:
3=1+2
4=1+3
5=1+4=2+3[可重复1次]
6=1+5=2+4[可重复1次]
7=1+6=2+5=3+4[可重复2次]
8=2+6=3+5[可重复1次]
9=3+6=4+5[可重复1次]
10=4+6
11=5+6
如果所有重复的情况都出现,这些重复的数字的和为:
2×(5+6+8+9)+3×7=56+21=77
12个和数字的和恒为84,剩余一个和数=84﹣77=7,而7已经被重复了2次,不可能再出现.
所以这种情况不成立.
所以最多只能重复5次.
即:棱上和数最少7个.
故答案为:A. 【分析】根据题意,相邻两面上的数相加,正方体每个面都有4个相邻面,所以每个面的数字都是加4遍,故不论数字怎么摆放,12条棱12个数字的和恒等于:4×21=84,这6个数任取2个相加,只有9个不重复的数字:3,4,5,6,7,8,9,10,11,棱上不同和数的个数最多9个!9个和数3,4,5,6,7,8,9,10,11分解:如果所有重复的情况都出现,这些重复的数字的和为:77,12个和数字的和恒为84,剩余一个和数=84﹣77=7,而7已经被重复了2次,不可能再出现,从而排除此种情况不成立,故最多只能重复5次,棱上和数最少7个.www.21-cn-jy.com
11. B
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴x与1是相对面,
∴x表示的数是﹣1,
故答案为:B.
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,然后确定出相对面,即x与1是相对面。又由于相对面上的两个数互为相反数,据此求解x。2·1·c·n·j·y
12.ABE
解:沿后面下面剪开可得E,沿后面右面剪开可得A,沿下面右面剪开即可得B, 故答案为:A,B,E.【来源:21·世纪·教育·网】
【分析】根据正方体展开图的特点,结合本题实际情况,即可得出答案。
一、基础巩固
1.长方形剪去一个角后所得的图形一定不是(? )
A.?五边形?????????????????????????????????B.?梯形?????????????????????????????????C.?长方形?????????????????????????????????D.?三角形
2.图中的几何体有(?? )条棱.
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
3.观察下列实物模型,其形状是圆柱体的是(?? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.下列图形属于圆锥的是(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
5.下面几何图形是平面图形的是(???? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
6.写出下图中各个几何体的名称,并按锥体和柱体把它们分类.
二、强化提升
7.某正方体的平面展开图如图所示,则原正方体中与“春”字所在的面相对的面上的字是(??? )
A.?青?????????????????????????????????????????B.?来?????????????????????????????????????????C.?斗?????????????????????????????????????????D.?奋
8.下列哪个图形是正方体的展开图( ??)
A.??????????????B.??????????????C.??????????????D.?
9.如图是一个几何体的表面展开图,这个几何体是(???? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
10.将自然数1至6分别写在一个正方体的6个面上,然后把任意相邻两个面上的数之和写在这两个面的公共棱上.则在这个正方体中所有棱上不同数的个数的最小值和最大值分别是(?? )
A.?7,9???????????????????????????????????B.?6,9???????????????????????????????????C.?7,10???????????????????????????????????D.?3,11
11.如图是一个正方体的展开图,相对面上的两个数互为相反数,则x等于(?? )
A.?1?????????????????????????????????????????B.?﹣1?????????????????????????????????????????C.?﹣2?????????????????????????????????????????D.?2
12.如图是一个没有完全展开的正方体,若再剪开一条棱,则得到的平面展开图可能是下图中的________(填写字母)21世纪教育网版权所有
答案解析部分
一、基础巩固
1. C
解:如图 当截线为经过正方形对角2个顶点的直线时,剩余图形为三角形(如图1); 当截线如图2所示,剩余图形是梯形(如图2); 当截线为只经过正方形一组邻边的一条直线时,剩余图形是五边形(如图3). 故不可能是长方形。 故答案为:C 21教育网
【分析】分情况讨论:当截线为经过正方形对角2个顶点的直线时如图1;当截线如图2所示;当截线为只经过正方形一组邻边的一条直线时,如图3,观察图形即可得出答案。21cnjy.com
2. D
解:此几何体有6条棱,
故答案为:D. 【分析】由图即可找出几何体的棱的数量。
3. D
解:圆柱的上下底面都是圆,所以正确的是D。 故答案为:D。 【分析】根据立体图形的特点及概念即可一一判断得出答案。21·cn·jy·com
4. C
A、此立体图形是四棱锥,不符合题意;
B、此立体图形是圆柱,不符合题意;
C、此立体图形是圆锥,符合题意;
D、此立体图形是直三棱柱,不符合题意;
故答案为:C. 【分析】根据圆锥、圆柱、棱柱、棱锥的特点分别分析即可求解.
5. A
解:由平面图形和立体图形的定义可知:A是平面图形,B、C、D是立体图形,
故答案为:A. 【分析】根据平面图形和立体图形的定义可求解.
6. 解:①圆柱②圆锥③四棱锥④五棱柱⑤三棱锥⑥四棱柱(或长方体)锥体有:②③⑤柱体有:①④⑥
【分析】柱体包括圆柱与棱柱,椎体包括圆锥和棱锥。棱柱:两底面是对应边平行的全等多边形,侧面,对角面都是平行四边形,侧棱平行且相等。圆柱:两个大小相同、互相平行的圆形底面,以及一个侧曲面。棱锥:侧面,对角面都是三角形。圆锥:有个圆形底面,侧面展开图是扇形。
二、强化提升
7. D
解:“ ”字型对面,可知春字对应的面上的字是奋;
故答案为:D.
【分析】根据正方体展开图的“Z”字型找对面的方法,就可得到答案。
8. B
解:根据正方形展开图的特征,只有选项B是正方体的展开图.
故答案为:B。 【分析】根据正方体展开图的11种特征,B选项属于中正方体展开图的“1-3-2”型,只有B符合.
9. C
解:由平面图形的折叠及三棱柱的展开图的特征可知,这个几何体是三棱柱.
故答案为:C. 【分析】由平面图形的折叠以及四个选项中的立体图形的展开图的特征即可作出判断。
10. A
证明:①根据题意,相邻两面上的数相加,正方体每个面都有4个相邻面,
所以:每个面的数字都是加4遍; 1、2、3、4、5、6这6个数的和为21;
所以:不论数字怎么摆放,12条棱12个数字的和恒等于:4×21=84
这6个数任取2个相加,只有9个不重复的数字:3,4,5,6,7,8,9,10,11
所以:根据“抽屉原理”,12条棱的数字至少重复3个.
即:棱上不同和数的个数最多9个! ②9个和数3,4,5,6,7,8,9,10,11分解:
3=1+2
4=1+3
5=1+4=2+3[可重复1次]
6=1+5=2+4[可重复1次]
7=1+6=2+5=3+4[可重复2次]
8=2+6=3+5[可重复1次]
9=3+6=4+5[可重复1次]
10=4+6
11=5+6
如果所有重复的情况都出现,这些重复的数字的和为:
2×(5+6+8+9)+3×7=56+21=77
12个和数字的和恒为84,剩余一个和数=84﹣77=7,而7已经被重复了2次,不可能再出现.
所以这种情况不成立.
所以最多只能重复5次.
即:棱上和数最少7个.
故答案为:A. 【分析】根据题意,相邻两面上的数相加,正方体每个面都有4个相邻面,所以每个面的数字都是加4遍,故不论数字怎么摆放,12条棱12个数字的和恒等于:4×21=84,这6个数任取2个相加,只有9个不重复的数字:3,4,5,6,7,8,9,10,11,棱上不同和数的个数最多9个!9个和数3,4,5,6,7,8,9,10,11分解:如果所有重复的情况都出现,这些重复的数字的和为:77,12个和数字的和恒为84,剩余一个和数=84﹣77=7,而7已经被重复了2次,不可能再出现,从而排除此种情况不成立,故最多只能重复5次,棱上和数最少7个.www.21-cn-jy.com
11. B
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴x与1是相对面,
∴x表示的数是﹣1,
故答案为:B.
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,然后确定出相对面,即x与1是相对面。又由于相对面上的两个数互为相反数,据此求解x。2·1·c·n·j·y
12.ABE
解:沿后面下面剪开可得E,沿后面右面剪开可得A,沿下面右面剪开即可得B, 故答案为:A,B,E.【来源:21·世纪·教育·网】
【分析】根据正方体展开图的特点,结合本题实际情况,即可得出答案。
