湘教版七年级数学上册第4章 图形的认识4.3.1 角与角的大小比较教学课件(共34张)
文档属性
| 名称 | 湘教版七年级数学上册第4章 图形的认识4.3.1 角与角的大小比较教学课件(共34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-11 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
角与角的大小比较
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
思考:这些实物带给我们的共同印象是什么呢?
新课导入
这些生活中的常见物品都包含了很多的不同大小的“角”
今天,就让我们来探究一下如何判断哪个角大,哪个角小。
02 新知探究
新知探究
观察角的图像,你能归纳出角的概念吗?尝试去描述一下角是由什么组成的图形?
角的定义及表示方法
新知探究
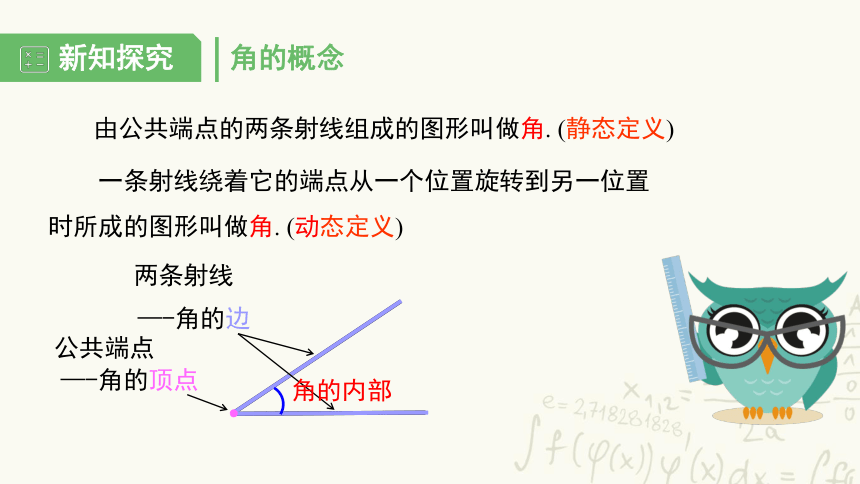
角的概念
由公共端点的两条射线组成的图形叫做角. (静态定义)
一条射线绕着它的端点从一个位置旋转到另一位置时所成的图形叫做角. (动态定义)
公共端点
—-角的顶点
两条射线
—-角的边
角的内部
新知探究
小归纳
O
A
B
O
A
(B)
平角
周角
O
A
B
(B)
平角的两边成一条直线.
周角的两边重合成一条射线.
当射线绕端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
当射线绕端点旋转一周,又重新回到原来的位置时,所成的角叫做周角.
新知探究
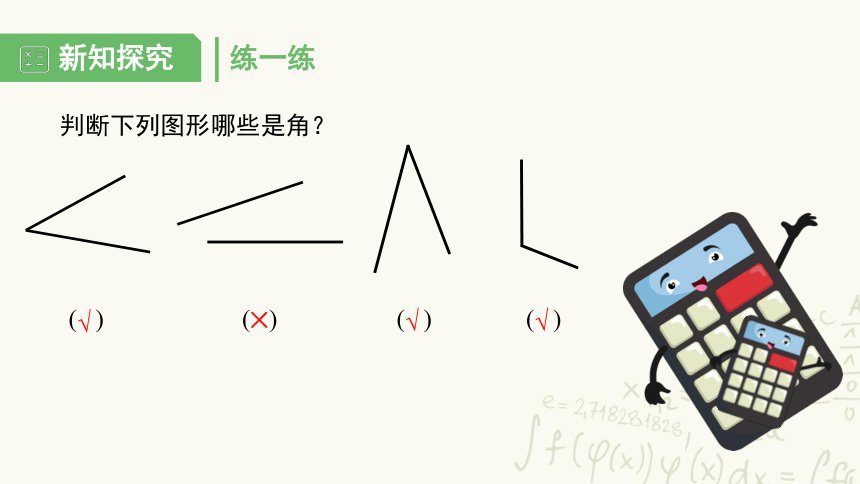
练一练
判断下列图形哪些是角?
( ) ( ) ( ) ( )
√
×
√
√
新知探究
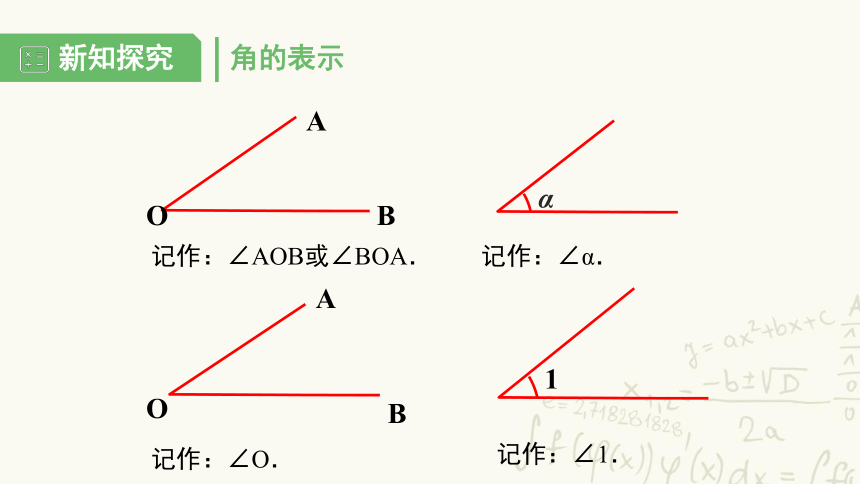
角的表示
A
O
B
记作:∠AOB或∠BOA.
A
O
B
记作:∠O.
α
记作:∠α.
1
记作:∠1.
新知探究
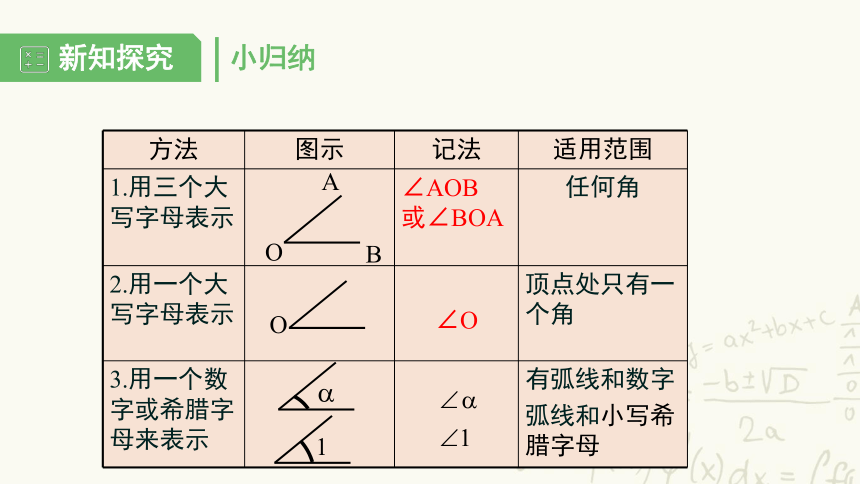
小归纳
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
新知探究
比较角的大小
类比线段长短的比较方法,你认为该如何比较两个角的大小?
角的大小比较:度量法、叠合法
新知探究
小归纳
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那∠DO'C___∠AOB.
=
>
<
O'
C
D
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
新知探究
想一想
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
新知探究
结论:角的两边张开越大,角就越大,与所画边的长短无关.
新知探究
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
角平分线
新知探究
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
新知探究
练一练
如图,若∠AOC=∠BOD,那么∠AOD与
∠BOC的关系是( )
A.∠AOD>∠BOC
B.∠AOD<∠BOC
C.∠AOD=∠BOC
D.无法确定
C
新知探究
动脑筋
如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
03 典型例题
典型例题
1.如图,下面的表示方法对不对,如果错了,应该怎样改正?
(1)图中的∠1表示成∠A;
(2)图中的∠2表示成∠D;
(3)图中的∠3表示成∠C.
解:(1)图中的∠1表示成∠DAC;
(2)图中的∠2表示成∠ADC;
(3)图中的∠3表示成∠ECF.
2.根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小;
(2)在图中找出角的三个等量关系.
解:(1)由图可知∠AOB>∠AOC>∠AOD>∠AOE.
(2)等量关系:
∠COE=∠EOD+∠COD,
∠AOB=∠AOE+∠BOE,
∠DOB=∠COD+∠BOC等.
典型例题
类似地,∠AOC-∠AOB= .
A
B
O
C
3.图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
它们的关系:
∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC-∠BOC;
∠BOC
∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;
典型例题
4.判断
(1) 直线是一个平角 ( )
(2) 如图①,点 P 不在 ∠AOB 的内部 ( )
(3) 如图②, ∠ABC与∠DBE是同一个角 ( )
A
O
B
·
P
D
A
B
C
·
E
·
×
×
图① 图②
√
典型例题
5.选择
(1)下列语句正确的是 ( )
A. 两条直线相交,组成的图形叫做角
B. 两条有公共端点的线段组成的图形叫做角
C. 两条有公共点的射线组成的图形叫做角
D. 从同一点引出的两条射线组成的图形叫做角
D
(2)下列说法不正确的是 ( )
A. ∠AOB 的顶点是O
B. 射线BO,AO分别是∠AOB的两条边
C. ∠AOB的边是两条射线
D. ∠AOB与∠BOA表示同一个角
B
典型例题
04 拓展提高
拓展提高
1.如图所示:
(1) 图中共有多少个角?请写出能用一个字母表示的角;
(2) 把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
答案:8个;∠A,∠O.
答案:∠A,∠O,∠1,
∠2,∠3,∠4,
∠ABC,∠ACB.
拓展提高
(3) 如图∠AOB内部画1条射线,问图中一共有多少个角?如果是画2条、3条呢?
(4) ∠AOB内部画99条射线,问图中一共有多少个角?如果是 (n-1)条呢?
答案:5050个,(1+2+3+…+n)个.
A
O
B
答案:3个,6个,10个.
A
O
B
…
05 课堂小结
课堂小结
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
06 作业布置
作业布置
熟记:1、角的定义及角的比较方法
2、完成课后习题1-3
谢 谢 观 看
角与角的大小比较
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
思考:这些实物带给我们的共同印象是什么呢?
新课导入
这些生活中的常见物品都包含了很多的不同大小的“角”
今天,就让我们来探究一下如何判断哪个角大,哪个角小。
02 新知探究
新知探究
观察角的图像,你能归纳出角的概念吗?尝试去描述一下角是由什么组成的图形?
角的定义及表示方法
新知探究
角的概念
由公共端点的两条射线组成的图形叫做角. (静态定义)
一条射线绕着它的端点从一个位置旋转到另一位置时所成的图形叫做角. (动态定义)
公共端点
—-角的顶点
两条射线
—-角的边
角的内部
新知探究
小归纳
O
A
B
O
A
(B)
平角
周角
O
A
B
(B)
平角的两边成一条直线.
周角的两边重合成一条射线.
当射线绕端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
当射线绕端点旋转一周,又重新回到原来的位置时,所成的角叫做周角.
新知探究
练一练
判断下列图形哪些是角?
( ) ( ) ( ) ( )
√
×
√
√
新知探究
角的表示
A
O
B
记作:∠AOB或∠BOA.
A
O
B
记作:∠O.
α
记作:∠α.
1
记作:∠1.
新知探究
小归纳
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
新知探究
比较角的大小
类比线段长短的比较方法,你认为该如何比较两个角的大小?
角的大小比较:度量法、叠合法
新知探究
小归纳
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那∠DO'C___∠AOB.
=
>
<
O'
C
D
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
新知探究
想一想
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
新知探究
结论:角的两边张开越大,角就越大,与所画边的长短无关.
新知探究
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
角平分线
新知探究
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
新知探究
练一练
如图,若∠AOC=∠BOD,那么∠AOD与
∠BOC的关系是( )
A.∠AOD>∠BOC
B.∠AOD<∠BOC
C.∠AOD=∠BOC
D.无法确定
C
新知探究
动脑筋
如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
03 典型例题
典型例题
1.如图,下面的表示方法对不对,如果错了,应该怎样改正?
(1)图中的∠1表示成∠A;
(2)图中的∠2表示成∠D;
(3)图中的∠3表示成∠C.
解:(1)图中的∠1表示成∠DAC;
(2)图中的∠2表示成∠ADC;
(3)图中的∠3表示成∠ECF.
2.根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小;
(2)在图中找出角的三个等量关系.
解:(1)由图可知∠AOB>∠AOC>∠AOD>∠AOE.
(2)等量关系:
∠COE=∠EOD+∠COD,
∠AOB=∠AOE+∠BOE,
∠DOB=∠COD+∠BOC等.
典型例题
类似地,∠AOC-∠AOB= .
A
B
O
C
3.图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
它们的关系:
∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC-∠BOC;
∠BOC
∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;
典型例题
4.判断
(1) 直线是一个平角 ( )
(2) 如图①,点 P 不在 ∠AOB 的内部 ( )
(3) 如图②, ∠ABC与∠DBE是同一个角 ( )
A
O
B
·
P
D
A
B
C
·
E
·
×
×
图① 图②
√
典型例题
5.选择
(1)下列语句正确的是 ( )
A. 两条直线相交,组成的图形叫做角
B. 两条有公共端点的线段组成的图形叫做角
C. 两条有公共点的射线组成的图形叫做角
D. 从同一点引出的两条射线组成的图形叫做角
D
(2)下列说法不正确的是 ( )
A. ∠AOB 的顶点是O
B. 射线BO,AO分别是∠AOB的两条边
C. ∠AOB的边是两条射线
D. ∠AOB与∠BOA表示同一个角
B
典型例题
04 拓展提高
拓展提高
1.如图所示:
(1) 图中共有多少个角?请写出能用一个字母表示的角;
(2) 把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
答案:8个;∠A,∠O.
答案:∠A,∠O,∠1,
∠2,∠3,∠4,
∠ABC,∠ACB.
拓展提高
(3) 如图∠AOB内部画1条射线,问图中一共有多少个角?如果是画2条、3条呢?
(4) ∠AOB内部画99条射线,问图中一共有多少个角?如果是 (n-1)条呢?
答案:5050个,(1+2+3+…+n)个.
A
O
B
答案:3个,6个,10个.
A
O
B
…
05 课堂小结
课堂小结
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
06 作业布置
作业布置
熟记:1、角的定义及角的比较方法
2、完成课后习题1-3
谢 谢 观 看
同课章节目录
