江苏省常州市2020届高三上学期期中考试数学文试题(PDF版)
文档属性
| 名称 | 江苏省常州市2020届高三上学期期中考试数学文试题(PDF版) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-10 12:39:39 | ||
图片预览




文档简介
11.若f(x)=C0sx-snx在[-a上是减函数,则a的最大值是▲
2.已知a,b为正实数,且(a+b)(+2b)+2a+3b=3,则3+4b的最小值为
13、已知圆O的半径为2,若PA、PB为该圆的两条切线,其中A、B为两切点,
则PAPB的最小值为
4.设函数f(x)=a-a-2-2x(a>e且a为常数,其中e为自然对数的底数)
则不等式(
g1x-1)≤0的解集是
解答题;(本大题共6小题,共计90分,请把答案写在答题卡相应的位置上.解
答时应写出文字说明,证明这程或演算步聚.)
15.(本小题满分14分)
如图,在直三棱柱ABC-A1BC中,AC=BC,AA1=AB,D为BB1的中点,E为AB1
上的一点,且AE
证:DE∥平面ABC
(2)求证:DE⊥CD
2-B
16、(本小题满分14分)
如图,在△4BC中,D为边BC上的一点,BD=3,simB=5,c0∠ADC=3
)求边AD的长
2)若△ABC的面积为480,求角C的值
高三文科数学试卷第2页(共4页)
7.(本小题满分14分)
已知函数f(x)=3ax4-2(3a+1)x2+4x
(1)当a=时,求∫(x)的极值;
(2)若函数∫(x)在(-1)上是增函数,求实数a的取值范围
(本小题满分16分)
已知数列{an}和仇n}满足a=1,b=0,4an1=3an-bn+4,4bn=3bn-an-4
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列
2)求{a}和}的通项公式
(3)设cn=an2-b2,记Sn=∑cn证明:2sSn+cn<6
19.(本小题满分16分)
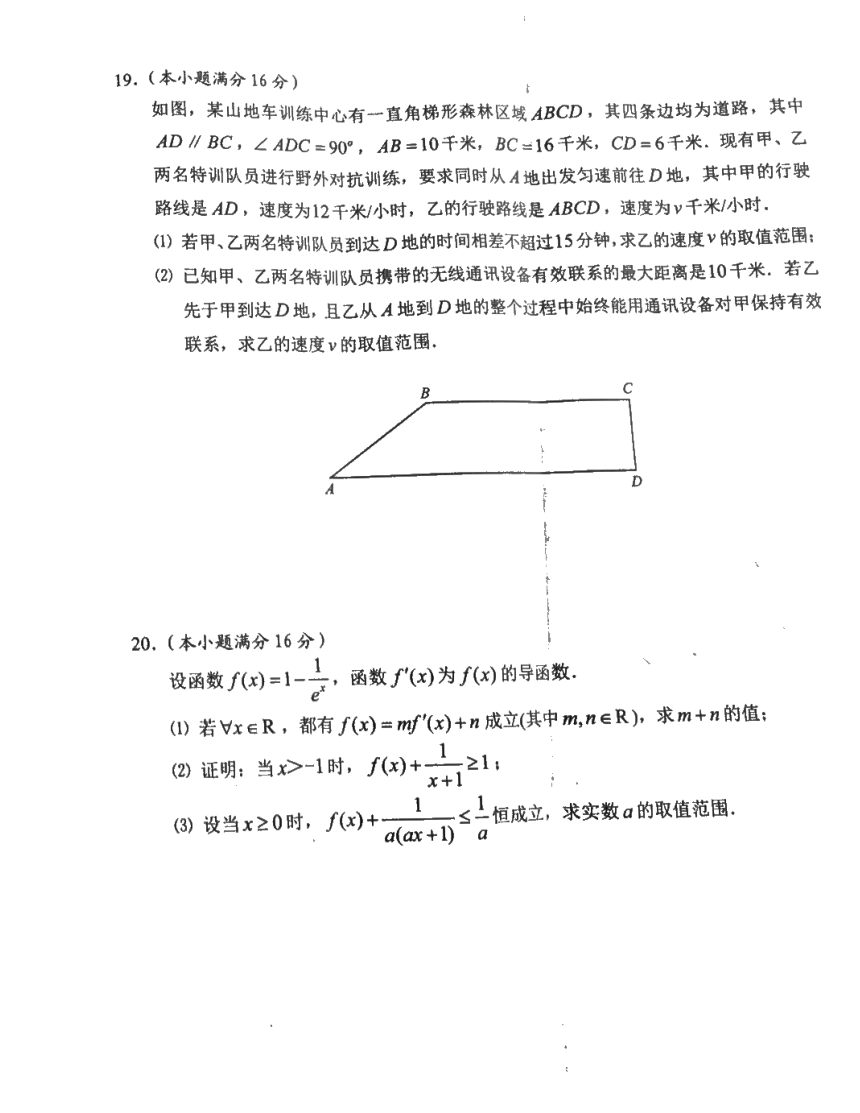
如图,某山地车训练中心有一直角梯形森林区域ABCD,其四条边均为道路,其中
AD∥BC,∠ADC=90°,AB=10千米,BC=16千米,CD=6千米.现有甲、乙
两名特训队员进行野外对抗训练,要求同时从A地出发匀速前往D地,其中甲的行驶
路线是AD,速度为12千米小时,乙的行驶路线是ABCD,速度为v千米小时
(1)若甲、乙两名特训队员到达D地的时间相差不超过15分钟,求乙的速度v的取值范围
(2)已知甲、乙两名特训队员携带的无线通讯设备有效联系的最大距离是10千米.若乙
先于甲到达D地,且乙从A地到D地的整个过程中始终能用通讯设备对甲保持有效
联系,求乙的速度ν的取值范围
20,(本小题满分16分)
设函数f(x)=1--,函数∫(x)为f(x)的导函数
(1)若vx∈R,都有f(x)=m(x)+n成立(其中m,n∈R),求m+n的值
(2)证明:当x>-1时,f(x)+
x+1
(3)设当x≥0时,∫(x)+
≤-恒成立,求实数a的取值范围
a(ax+1)
2.已知a,b为正实数,且(a+b)(+2b)+2a+3b=3,则3+4b的最小值为
13、已知圆O的半径为2,若PA、PB为该圆的两条切线,其中A、B为两切点,
则PAPB的最小值为
4.设函数f(x)=a-a-2-2x(a>e且a为常数,其中e为自然对数的底数)
则不等式(
g1x-1)≤0的解集是
解答题;(本大题共6小题,共计90分,请把答案写在答题卡相应的位置上.解
答时应写出文字说明,证明这程或演算步聚.)
15.(本小题满分14分)
如图,在直三棱柱ABC-A1BC中,AC=BC,AA1=AB,D为BB1的中点,E为AB1
上的一点,且AE
证:DE∥平面ABC
(2)求证:DE⊥CD
2-B
16、(本小题满分14分)
如图,在△4BC中,D为边BC上的一点,BD=3,simB=5,c0∠ADC=3
)求边AD的长
2)若△ABC的面积为480,求角C的值
高三文科数学试卷第2页(共4页)
7.(本小题满分14分)
已知函数f(x)=3ax4-2(3a+1)x2+4x
(1)当a=时,求∫(x)的极值;
(2)若函数∫(x)在(-1)上是增函数,求实数a的取值范围
(本小题满分16分)
已知数列{an}和仇n}满足a=1,b=0,4an1=3an-bn+4,4bn=3bn-an-4
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列
2)求{a}和}的通项公式
(3)设cn=an2-b2,记Sn=∑cn证明:2sSn+cn<6
19.(本小题满分16分)
如图,某山地车训练中心有一直角梯形森林区域ABCD,其四条边均为道路,其中
AD∥BC,∠ADC=90°,AB=10千米,BC=16千米,CD=6千米.现有甲、乙
两名特训队员进行野外对抗训练,要求同时从A地出发匀速前往D地,其中甲的行驶
路线是AD,速度为12千米小时,乙的行驶路线是ABCD,速度为v千米小时
(1)若甲、乙两名特训队员到达D地的时间相差不超过15分钟,求乙的速度v的取值范围
(2)已知甲、乙两名特训队员携带的无线通讯设备有效联系的最大距离是10千米.若乙
先于甲到达D地,且乙从A地到D地的整个过程中始终能用通讯设备对甲保持有效
联系,求乙的速度ν的取值范围
20,(本小题满分16分)
设函数f(x)=1--,函数∫(x)为f(x)的导函数
(1)若vx∈R,都有f(x)=m(x)+n成立(其中m,n∈R),求m+n的值
(2)证明:当x>-1时,f(x)+
x+1
(3)设当x≥0时,∫(x)+
≤-恒成立,求实数a的取值范围
a(ax+1)
同课章节目录
