高中数学北师大版必修3课件:2.2.1 顺序结构与选择结构 :30张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:2.2.1 顺序结构与选择结构 :30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 920.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-10 00:00:00 | ||
图片预览






文档简介
课件30张PPT。2.1 顺序结构与选择结构1.算法框图
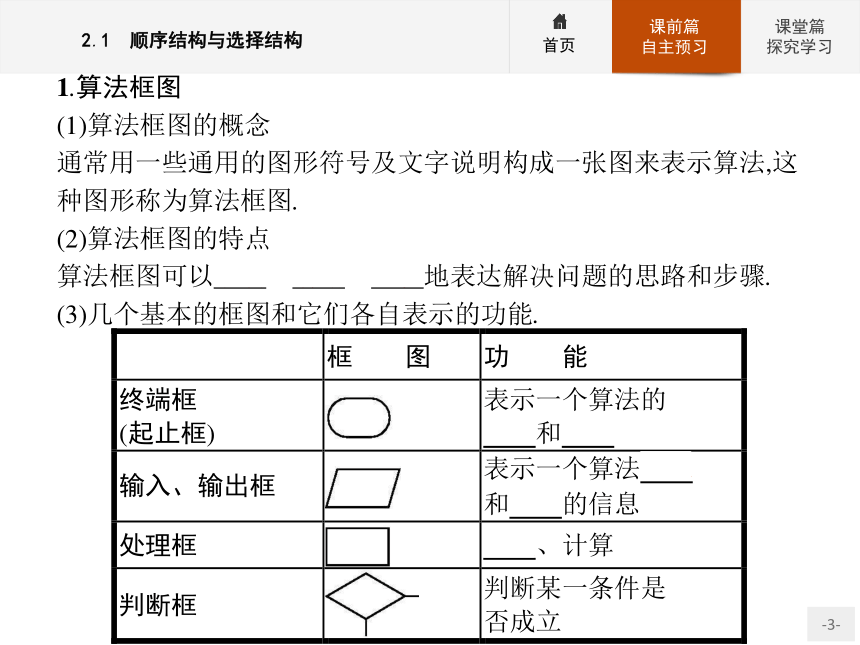
(1)算法框图的概念
通常用一些通用的图形符号及文字说明构成一张图来表示算法,这种图形称为算法框图.
(2)算法框图的特点
算法框图可以准确、清晰、直观地表达解决问题的思路和步骤.
(3)几个基本的框图和它们各自表示的功能.(4)算法框图的基本结构
算法框图有三种基本结构:顺序结构、选择结构和循环结构.【做一做1】 下列关于算法框图的说法正确的是 ( )
①算法框图只有一个入口,也只有一个出口;
②算法框图中的每一部分都应有一条从入口到出口的路径通过它;
③流程线只要是从上到下方向就表示上下执行,可以不要箭头;
④连接点是用来连接两个算法框图的.
A.①②③ B.②③ C.①④ D.①②
解析:由框图符号及作用可知③④错误,流程线表示算法步骤执行的顺序,用来连接算法框图,是带箭头的直线或折线,应用时必须带箭头;连接点是连接同一个算法框图的不同部分的.
答案:D规律总结画算法框图的规则
(1)使用标准的框图符号;
(2)框图一般按从上到下,从左到右的方向画;
(3)除判断框外,大多数框图符号只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号;
(4)在图形符号内描述的语言要简练准确.2.顺序结构
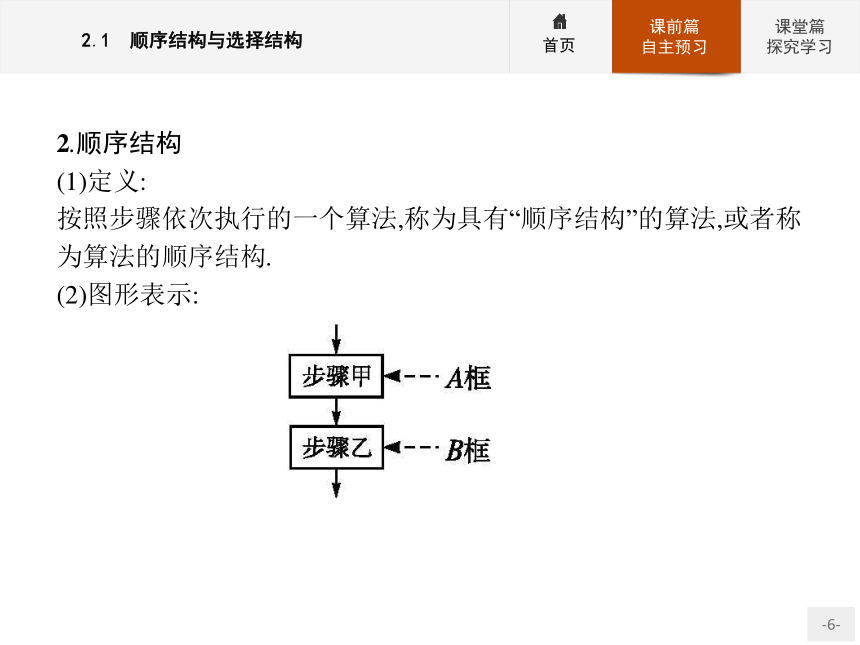
(1)定义:
按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.?
(2)图形表示:(3)特点:
①顺序结构是最简单的算法结构,它按自上而下的顺序依次执行,不会引起算法步骤的跳转.
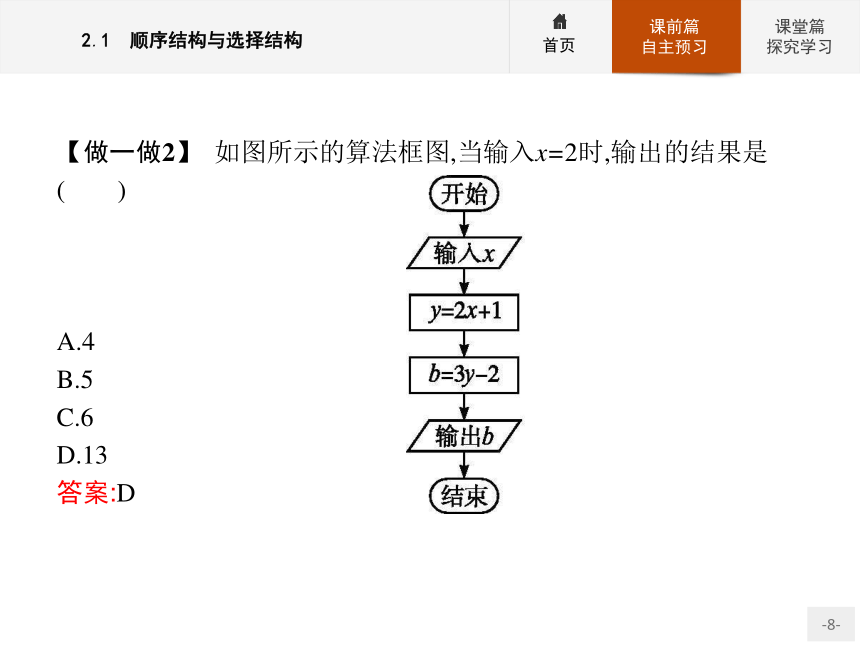
②顺序结构在算法框图中的体现就是用流程线将算法框自上而下地连接起来、按顺序执行算法步骤.如图,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.【做一做2】 如图所示的算法框图,当输入x=2时,输出的结果是( )
A.4
B.5
C.6
D.13
答案:D3.选择结构
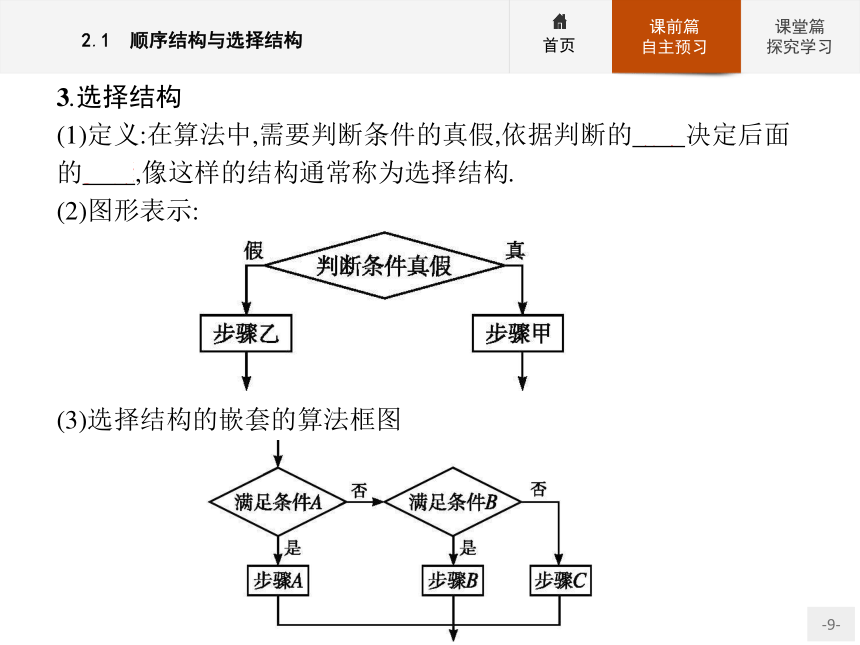
(1)定义:在算法中,需要判断条件的真假,依据判断的结果决定后面的步骤,像这样的结构通常称为选择结构.
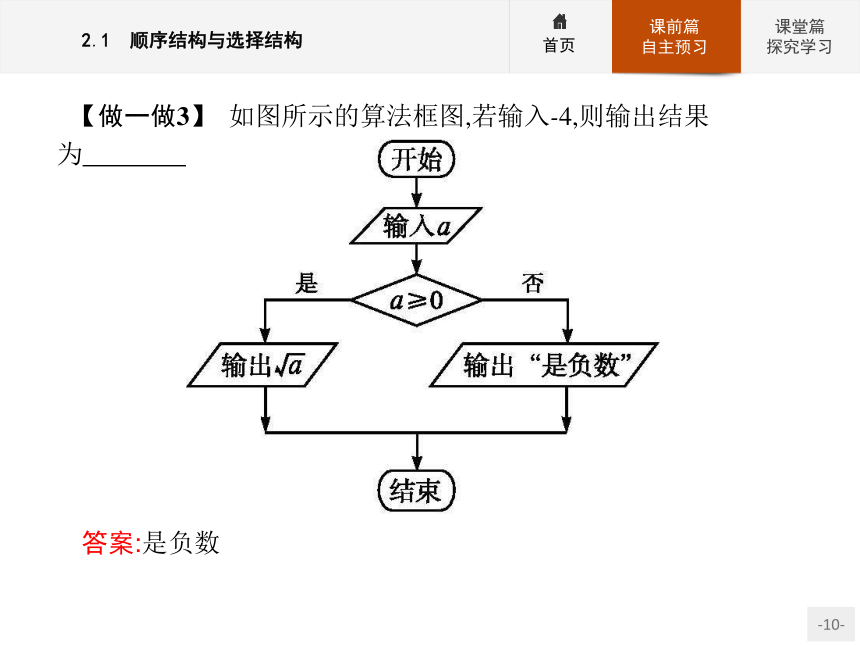
(2)图形表示:(3)选择结构的嵌套的算法框图 【做一做3】 如图所示的算法框图,若输入-4,则输出结果为 .?答案:是负数 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)一个算法只能对应一个算法框图. ( )
(2)一个算法中必须同时有顺序结构和选择结构. ( )
(3)选择结构中必须要含有判断框. ( )
(4)选择结构被执行时,判断框的两个出口有且只有一个被执行,不可能两个出口同时被执行,也不可能两个出口都不被执行. ( )
答案:(1)× (2)× (3)√ (4)√探究一探究二探究三思维辨析当堂检测 顺序结构的算法设计及算法框图
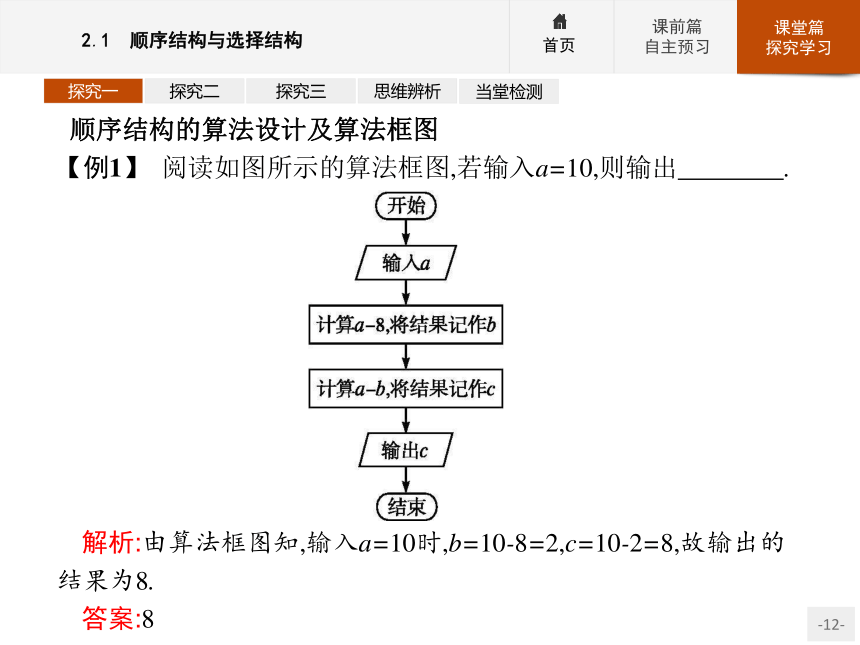
【例1】 阅读如图所示的算法框图,若输入a=10,则输出 .解析:由算法框图知,输入a=10时,b=10-8=2,c=10-2=8,故输出的结果为8.
答案:8探究一探究二探究三思维辨析当堂检测反思感悟1.顺序结构是任何一个算法都离不开的最基本、最简单的基本结构,其算法框图中不含有判断框.
2.对于套用公式求解问题往往运用顺序结构.编写顺序结构的算法,应写出公式,看公式中的条件是否满足,若不满足先求出需要的量,再将公式中涉及的量全部代入求值即可.
3.画顺序结构的算法框图时,一般按照“输入(赋值)—运算—输出”的顺序设计.探究一探究二探究三思维辨析当堂检测变式训练1(2018甘肃兰州高一同步检测)如图所示,图①是计算图②中空白部分面积的一个算法框图,则“?”处应填 .?探究一探究二探究三思维辨析当堂检测 选择结构的算法设计及算法框图【例2】 设计输入一个数x,求分段函数 的函数值的算法框图.
分析分段函数求值,首先要判断自变量x的所在范围,然后选择对应解析式.首先写出其算法,然后利用算法框图表示相应的算法.
解算法如下:
1.输入x;
2.若x<0,则y=ex;
否则,y= ;
3.输出y.
算法框图如图所示.探究一探究二探究三思维辨析当堂检测反思感悟选择结构的一般模式如图①、图②所示.(1)在图①所示的选择结构中,根据给定的条件P是否成立而选择执行A框或B框.请注意,无论条件P是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框,也不可能A框、B框都不执行.无论走哪一条路径,在执行完A或B之后,都要脱离本选择结构.
(2)在A或B两个框中,可以有一个是空的(如图②),即不执行任何操作.探究一探究二探究三思维辨析当堂检测 变式训练2(1)给出以下四个问题:
①输入一个数x,输出它的相反数.
②求面积为6的正方形的周长.
③求三个数a,b,c中的最大数.其中不需要用选择结构来描述其算法的有( )
A.1个 B.2个 C.3个 D.4个
(2)某居民区的物业部门每月向居民收取卫生费,计算方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,只需画出算法框图即可.探究一探究二探究三思维辨析当堂检测(1)答案:A
(2)解:依题意费用y与人数n之间的关系为算法框图如图所示: 探究一探究二探究三思维辨析当堂检测算法框图的应用
【例3】如图所示的算法框图,根据该图回答下面的问题:探究一探究二探究三思维辨析当堂检测(1)该算法框图解决的是一个什么问题?
(2)当输入x的值为0和4时,输出的值相等.
①当输入x的值为3时,输出的值为多少?
②要想使输出的值最大,输入x的值应为多少?
③按照这个算法框图输出f(x)的值,当x的值都大于2时,x越大输出f(x)的值反而越小,为什么?
④要想使输出的值等于3,输入x的值应为多少?
⑤要想使输入的值与输出的值相等,输入的值应该是多少?
分析:本题中的算法与二次函数有关,因此可借助二次函数的有关知识求解.探究一探究二探究三思维辨析当堂检测解:(1)该算法框图解决的是求二次函数f(x)=-x2+mx的函数值的问题.
(2)当输入x的值为0和4时,输出的值相等,
即f(0)=f(4).
∵f(0)=0,f(4)=-16+4m,
∴-16+4m=0.
∴m=4,
∴f(x)=-x2+4x.
①∵f(3)=-32+4×3=3,
∴当输入x的值为3时,输出的值为3.
②∵f(x)=-x2+4x=-(x-2)2+4,当x=2时,f(x)max=4.
∴要想使输出的值最大,输入x的值应为2.探究一探究二探究三思维辨析当堂检测③∵f(x)=-(x-2)2+4,
∴函数f(x)在[2,+∞)内是减少的.
∴在[2,+∞)内,x越大对应的函数值反而越小,从而当输入x的值大于2时,x越大输出f(x)的值反而越小.
④令f(x)=3,即-x2+4x=3,
解得x=1或x=3,
∴要想使输出的值等于3,输入x的值应为1或3.
⑤由f(x)=x,即-x2+4x=x,
解得x=0或x=3.
∴要使输入的值与输出的值相等,输入x的值应为0或3.
反思感悟给出算法框图时,要准确理解框图中各个图形符号的含义及其功能,明确各个框、各部分的功能和作用,从而理解整个算法框图的意义,明确其对应算法的功能,有时要与函数的相关知识结合起来.探究一探究二探究三思维辨析当堂检测 变式训练3阅读如下的算法框图,判断下列说法:
?
①该框图中含有顺序结构和选择结构;
②该框图中只含有选择结构;
③当输入x=2时,输出结果为2;
④当输出结果为0时,输入x=-2.
其中正确的说法是 .?
解析:由框图可知,该算法框图中含有顺序结构和选择结构,故①正确,②不正确;当x=2时,由于2>2不成立,应输出2+2=4,故③不正确;当输出结果为0时,由于0<2,因此x+2=0,即x=-2,故④正确.
答案:①④探究一探究二探究三思维辨析当堂检测忽视判断框内的条件而致误
【典例】 已知算法框图如下:若输出y的值为4,则输入x的值为 .?探究一探究二探究三思维辨析当堂检测纠错心得本题错误的根源在于忽视了判断框内的条件,要明确类似这种根据函数值求自变量x的问题注意对x的值进行取舍.探究一探究二探究三思维辨析当堂检测 变式训练如图所示的算法框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( )
?
A.c>x B.x>c
C.c>b D.b>c
解析:第1个判断框比较a与b的大小,第2个判断框比较a与b中的较大者与c的关系,应为c>x.
答案:A探究一探究二探究三思维辨析当堂检测1.选择结构不同于顺序结构的一个特征是其一定含有 ( )
A.处理框 B.判断框
C.输入框 D.起止框
答案:B
2.如图所示的算法框图,能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
?
A.m=0 B.x=0
C.x=1 D.m=1
答案:A探究一探究二探究三思维辨析当堂检测3.如图所示的算法框图,若输出的结果是S=7,则输入A的值为 .
解析:该算法框图的功能是输入A,计算2A+1的值.令2A+1=7,解得A=3.
答案:3探究一探究二探究三思维辨析当堂检测4.如图是一个算法框图,当输入的值为3时,输出的结果是 .答案:8 探究一探究二探究三思维辨析当堂检测5.若已知梯形上、下底边长和面积,求该梯形的高.
分析首先根据梯形面积公式列出方程,表示出梯形的高,然后根据高的表达式设计相应的算法,最后用算法框图语言表示相应的算法步骤.
解算法如下:
1.输入梯形的上、下底边长a,b和面积S.
2.计算a+b的值.
4.输出h.
算法框图如图所示:
(1)算法框图的概念
通常用一些通用的图形符号及文字说明构成一张图来表示算法,这种图形称为算法框图.
(2)算法框图的特点
算法框图可以准确、清晰、直观地表达解决问题的思路和步骤.
(3)几个基本的框图和它们各自表示的功能.(4)算法框图的基本结构
算法框图有三种基本结构:顺序结构、选择结构和循环结构.【做一做1】 下列关于算法框图的说法正确的是 ( )
①算法框图只有一个入口,也只有一个出口;
②算法框图中的每一部分都应有一条从入口到出口的路径通过它;
③流程线只要是从上到下方向就表示上下执行,可以不要箭头;
④连接点是用来连接两个算法框图的.
A.①②③ B.②③ C.①④ D.①②
解析:由框图符号及作用可知③④错误,流程线表示算法步骤执行的顺序,用来连接算法框图,是带箭头的直线或折线,应用时必须带箭头;连接点是连接同一个算法框图的不同部分的.
答案:D规律总结画算法框图的规则
(1)使用标准的框图符号;
(2)框图一般按从上到下,从左到右的方向画;
(3)除判断框外,大多数框图符号只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号;
(4)在图形符号内描述的语言要简练准确.2.顺序结构
(1)定义:
按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.?
(2)图形表示:(3)特点:
①顺序结构是最简单的算法结构,它按自上而下的顺序依次执行,不会引起算法步骤的跳转.
②顺序结构在算法框图中的体现就是用流程线将算法框自上而下地连接起来、按顺序执行算法步骤.如图,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.【做一做2】 如图所示的算法框图,当输入x=2时,输出的结果是( )
A.4
B.5
C.6
D.13
答案:D3.选择结构
(1)定义:在算法中,需要判断条件的真假,依据判断的结果决定后面的步骤,像这样的结构通常称为选择结构.
(2)图形表示:(3)选择结构的嵌套的算法框图 【做一做3】 如图所示的算法框图,若输入-4,则输出结果为 .?答案:是负数 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)一个算法只能对应一个算法框图. ( )
(2)一个算法中必须同时有顺序结构和选择结构. ( )
(3)选择结构中必须要含有判断框. ( )
(4)选择结构被执行时,判断框的两个出口有且只有一个被执行,不可能两个出口同时被执行,也不可能两个出口都不被执行. ( )
答案:(1)× (2)× (3)√ (4)√探究一探究二探究三思维辨析当堂检测 顺序结构的算法设计及算法框图
【例1】 阅读如图所示的算法框图,若输入a=10,则输出 .解析:由算法框图知,输入a=10时,b=10-8=2,c=10-2=8,故输出的结果为8.
答案:8探究一探究二探究三思维辨析当堂检测反思感悟1.顺序结构是任何一个算法都离不开的最基本、最简单的基本结构,其算法框图中不含有判断框.
2.对于套用公式求解问题往往运用顺序结构.编写顺序结构的算法,应写出公式,看公式中的条件是否满足,若不满足先求出需要的量,再将公式中涉及的量全部代入求值即可.
3.画顺序结构的算法框图时,一般按照“输入(赋值)—运算—输出”的顺序设计.探究一探究二探究三思维辨析当堂检测变式训练1(2018甘肃兰州高一同步检测)如图所示,图①是计算图②中空白部分面积的一个算法框图,则“?”处应填 .?探究一探究二探究三思维辨析当堂检测 选择结构的算法设计及算法框图【例2】 设计输入一个数x,求分段函数 的函数值的算法框图.
分析分段函数求值,首先要判断自变量x的所在范围,然后选择对应解析式.首先写出其算法,然后利用算法框图表示相应的算法.
解算法如下:
1.输入x;
2.若x<0,则y=ex;
否则,y= ;
3.输出y.
算法框图如图所示.探究一探究二探究三思维辨析当堂检测反思感悟选择结构的一般模式如图①、图②所示.(1)在图①所示的选择结构中,根据给定的条件P是否成立而选择执行A框或B框.请注意,无论条件P是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框,也不可能A框、B框都不执行.无论走哪一条路径,在执行完A或B之后,都要脱离本选择结构.
(2)在A或B两个框中,可以有一个是空的(如图②),即不执行任何操作.探究一探究二探究三思维辨析当堂检测 变式训练2(1)给出以下四个问题:
①输入一个数x,输出它的相反数.
②求面积为6的正方形的周长.
③求三个数a,b,c中的最大数.其中不需要用选择结构来描述其算法的有( )
A.1个 B.2个 C.3个 D.4个
(2)某居民区的物业部门每月向居民收取卫生费,计算方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,只需画出算法框图即可.探究一探究二探究三思维辨析当堂检测(1)答案:A
(2)解:依题意费用y与人数n之间的关系为算法框图如图所示: 探究一探究二探究三思维辨析当堂检测算法框图的应用
【例3】如图所示的算法框图,根据该图回答下面的问题:探究一探究二探究三思维辨析当堂检测(1)该算法框图解决的是一个什么问题?
(2)当输入x的值为0和4时,输出的值相等.
①当输入x的值为3时,输出的值为多少?
②要想使输出的值最大,输入x的值应为多少?
③按照这个算法框图输出f(x)的值,当x的值都大于2时,x越大输出f(x)的值反而越小,为什么?
④要想使输出的值等于3,输入x的值应为多少?
⑤要想使输入的值与输出的值相等,输入的值应该是多少?
分析:本题中的算法与二次函数有关,因此可借助二次函数的有关知识求解.探究一探究二探究三思维辨析当堂检测解:(1)该算法框图解决的是求二次函数f(x)=-x2+mx的函数值的问题.
(2)当输入x的值为0和4时,输出的值相等,
即f(0)=f(4).
∵f(0)=0,f(4)=-16+4m,
∴-16+4m=0.
∴m=4,
∴f(x)=-x2+4x.
①∵f(3)=-32+4×3=3,
∴当输入x的值为3时,输出的值为3.
②∵f(x)=-x2+4x=-(x-2)2+4,当x=2时,f(x)max=4.
∴要想使输出的值最大,输入x的值应为2.探究一探究二探究三思维辨析当堂检测③∵f(x)=-(x-2)2+4,
∴函数f(x)在[2,+∞)内是减少的.
∴在[2,+∞)内,x越大对应的函数值反而越小,从而当输入x的值大于2时,x越大输出f(x)的值反而越小.
④令f(x)=3,即-x2+4x=3,
解得x=1或x=3,
∴要想使输出的值等于3,输入x的值应为1或3.
⑤由f(x)=x,即-x2+4x=x,
解得x=0或x=3.
∴要使输入的值与输出的值相等,输入x的值应为0或3.
反思感悟给出算法框图时,要准确理解框图中各个图形符号的含义及其功能,明确各个框、各部分的功能和作用,从而理解整个算法框图的意义,明确其对应算法的功能,有时要与函数的相关知识结合起来.探究一探究二探究三思维辨析当堂检测 变式训练3阅读如下的算法框图,判断下列说法:
?
①该框图中含有顺序结构和选择结构;
②该框图中只含有选择结构;
③当输入x=2时,输出结果为2;
④当输出结果为0时,输入x=-2.
其中正确的说法是 .?
解析:由框图可知,该算法框图中含有顺序结构和选择结构,故①正确,②不正确;当x=2时,由于2>2不成立,应输出2+2=4,故③不正确;当输出结果为0时,由于0<2,因此x+2=0,即x=-2,故④正确.
答案:①④探究一探究二探究三思维辨析当堂检测忽视判断框内的条件而致误
【典例】 已知算法框图如下:若输出y的值为4,则输入x的值为 .?探究一探究二探究三思维辨析当堂检测纠错心得本题错误的根源在于忽视了判断框内的条件,要明确类似这种根据函数值求自变量x的问题注意对x的值进行取舍.探究一探究二探究三思维辨析当堂检测 变式训练如图所示的算法框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( )
?
A.c>x B.x>c
C.c>b D.b>c
解析:第1个判断框比较a与b的大小,第2个判断框比较a与b中的较大者与c的关系,应为c>x.
答案:A探究一探究二探究三思维辨析当堂检测1.选择结构不同于顺序结构的一个特征是其一定含有 ( )
A.处理框 B.判断框
C.输入框 D.起止框
答案:B
2.如图所示的算法框图,能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
?
A.m=0 B.x=0
C.x=1 D.m=1
答案:A探究一探究二探究三思维辨析当堂检测3.如图所示的算法框图,若输出的结果是S=7,则输入A的值为 .
解析:该算法框图的功能是输入A,计算2A+1的值.令2A+1=7,解得A=3.
答案:3探究一探究二探究三思维辨析当堂检测4.如图是一个算法框图,当输入的值为3时,输出的结果是 .答案:8 探究一探究二探究三思维辨析当堂检测5.若已知梯形上、下底边长和面积,求该梯形的高.
分析首先根据梯形面积公式列出方程,表示出梯形的高,然后根据高的表达式设计相应的算法,最后用算法框图语言表示相应的算法步骤.
解算法如下:
1.输入梯形的上、下底边长a,b和面积S.
2.计算a+b的值.
4.输出h.
算法框图如图所示:
