高中数学北师大版选修4-4课件:2.2.1 直线的参数方程 :21张PPT
文档属性
| 名称 | 高中数学北师大版选修4-4课件:2.2.1 直线的参数方程 :21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 773.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-12 00:00:00 | ||
图片预览








文档简介
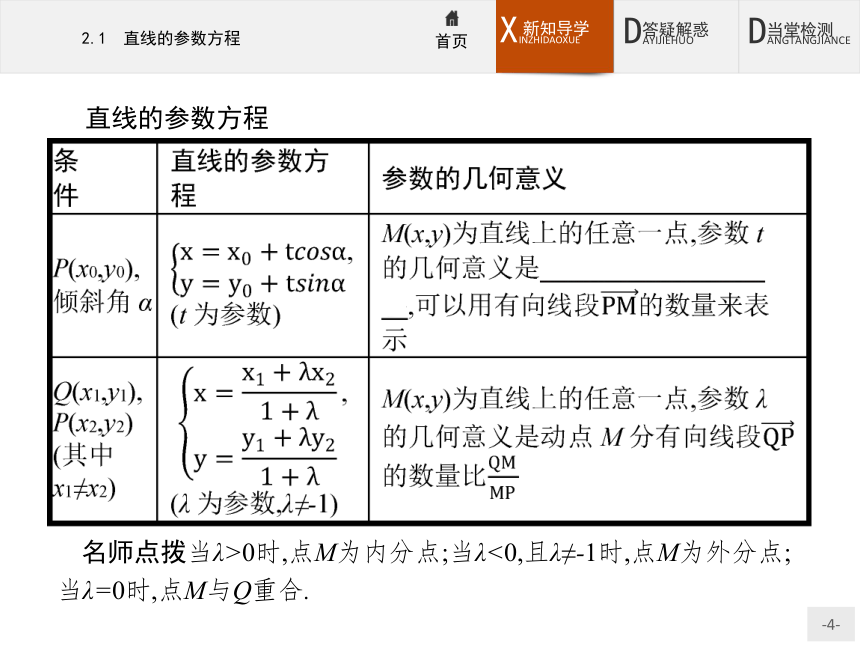
课件21张PPT。§2 直线和圆锥曲线的参数方程2.1 直线的参数方程直线的参数方程 名师点拨当λ>0时,点M为内分点;当λ<0,且λ≠-1时,点M为外分点;当λ=0时,点M与Q重合.做一做 直线 (t为参数)的倾斜角α等于( )?
A.30° B.60° C.-45° D.135°
解析:由参数方程知 两式相加,得直线的普通方
程x+y=1,倾斜角为α,则tan α=-1,所以α=135°.
答案:D思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)有方向的线段 的数量既可以为正值,也可以为负值. ( )√ × √ 探究一探究二思维辨析直线的参数方程与参数的几何意义?
【例1】 已知直线l的方程为3x-4y+1=0,点P(1,1)在直线l上,写出直线l的参数方程,并分别求出点P到点M(5,4)和点N(-2,6)的距离.探究一探究二思维辨析探究一探究二思维辨析反思感悟对于一般的参数方程,其中的参数可能不具有一定的几何意义,但是直线参数方程中的参数有一定的几何意义.过定点
M0(x0,y0)、倾斜角为α的直线l的参数方程都可以写成 (t为参数),其中直线上的动点M(x,y)到定点M0的距离等于参数t的绝对值.当点M在点M0的上方时,t>0;当点M在点M0的下方时,t<0;当点M与点M0重合时,t=0.很多与线段长度有关的问题,我们可以考虑应用直线参数方程中t的几何意义去求解.探究一探究二思维辨析变式训练1 一直线过点P0(3,4),倾斜角α= ,求此直线与直线3x+2y=6的交点M与点P0之间的距离.?探究一探究二思维辨析直线参数方程的应用?
【例2】 已知直线的参数方程为 (t为参数),则该直线被圆x2+y2=9截得的弦长是 .?探究一探究二思维辨析反思感悟设过定点P0的直线l与二次曲线f(x,y)=0相交于P,Q两点,将直线l的参数方程代入曲线方程f(x,y)=0,得到关于t的二次方程At2+Bt+C=0(A≠0).
设P,Q两点对应的参数分别为t1,t2,则t1,t2为上述方程的两根,(2)若点P0为PQ的中点,则有t1+t2=0,即B=0,P0对应参数t0= ;
(3)若点P0为PQ的一个三等分点,则有t1=-2t2或t2=-2t1.探究一探究二思维辨析变式训练2 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别相交于A,B两点,求|PA|·|PB|的值为最小时直线l的方程.探究一探究二思维辨析因未理解直线参数方程的标准形式而致误
典例直线 (t为参数)的倾斜角是 .?探究一探究二思维辨析答案:110° 消去t,得y=(x-3)tan 110°,
所以直线的倾斜角为110°.所以直线的倾斜角为110°. 探究一探究二思维辨析纠错心得1.本题未正确理解直线参数方程的标准形式,把 2.只有在 (t为参数)中,θ才表示直线的倾斜角.若不是这种形式,则需要进行转化.探究一探究二思维辨析变式训练 求直线 (t为参数)被双曲线x2-y2=1截得的弦长|AB|.?1 2 3 41.直线 (t为参数)上对应t=0,t=1两点间的距离是( )解析:因为题目所给方程不是参数方程的标准形式,参数t不具有几何意义,故不能直接由1-0=1来得距离,应将t=0,t=1分别代入方程得到两点坐标(2,-1)和(5,0),由两点间距离公式来求出距离,即
答案:B1 2 3 42.经过点Q(1,2),P(3,7)的直线的参数方程为( ) 答案:B 1 2 3 43.经过点M(-2,3),倾斜角为 的直线l的参数方程是 .?1 2 3 44.导学号64470031已知直线l:x+y-1=0与抛物线y=x2交于A,B两点,求线段AB的长和点M(-1,2)到A,B两点的距离之积.
A.30° B.60° C.-45° D.135°
解析:由参数方程知 两式相加,得直线的普通方
程x+y=1,倾斜角为α,则tan α=-1,所以α=135°.
答案:D思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)有方向的线段 的数量既可以为正值,也可以为负值. ( )√ × √ 探究一探究二思维辨析直线的参数方程与参数的几何意义?
【例1】 已知直线l的方程为3x-4y+1=0,点P(1,1)在直线l上,写出直线l的参数方程,并分别求出点P到点M(5,4)和点N(-2,6)的距离.探究一探究二思维辨析探究一探究二思维辨析反思感悟对于一般的参数方程,其中的参数可能不具有一定的几何意义,但是直线参数方程中的参数有一定的几何意义.过定点
M0(x0,y0)、倾斜角为α的直线l的参数方程都可以写成 (t为参数),其中直线上的动点M(x,y)到定点M0的距离等于参数t的绝对值.当点M在点M0的上方时,t>0;当点M在点M0的下方时,t<0;当点M与点M0重合时,t=0.很多与线段长度有关的问题,我们可以考虑应用直线参数方程中t的几何意义去求解.探究一探究二思维辨析变式训练1 一直线过点P0(3,4),倾斜角α= ,求此直线与直线3x+2y=6的交点M与点P0之间的距离.?探究一探究二思维辨析直线参数方程的应用?
【例2】 已知直线的参数方程为 (t为参数),则该直线被圆x2+y2=9截得的弦长是 .?探究一探究二思维辨析反思感悟设过定点P0的直线l与二次曲线f(x,y)=0相交于P,Q两点,将直线l的参数方程代入曲线方程f(x,y)=0,得到关于t的二次方程At2+Bt+C=0(A≠0).
设P,Q两点对应的参数分别为t1,t2,则t1,t2为上述方程的两根,(2)若点P0为PQ的中点,则有t1+t2=0,即B=0,P0对应参数t0= ;
(3)若点P0为PQ的一个三等分点,则有t1=-2t2或t2=-2t1.探究一探究二思维辨析变式训练2 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别相交于A,B两点,求|PA|·|PB|的值为最小时直线l的方程.探究一探究二思维辨析因未理解直线参数方程的标准形式而致误
典例直线 (t为参数)的倾斜角是 .?探究一探究二思维辨析答案:110° 消去t,得y=(x-3)tan 110°,
所以直线的倾斜角为110°.所以直线的倾斜角为110°. 探究一探究二思维辨析纠错心得1.本题未正确理解直线参数方程的标准形式,把 2.只有在 (t为参数)中,θ才表示直线的倾斜角.若不是这种形式,则需要进行转化.探究一探究二思维辨析变式训练 求直线 (t为参数)被双曲线x2-y2=1截得的弦长|AB|.?1 2 3 41.直线 (t为参数)上对应t=0,t=1两点间的距离是( )解析:因为题目所给方程不是参数方程的标准形式,参数t不具有几何意义,故不能直接由1-0=1来得距离,应将t=0,t=1分别代入方程得到两点坐标(2,-1)和(5,0),由两点间距离公式来求出距离,即
答案:B1 2 3 42.经过点Q(1,2),P(3,7)的直线的参数方程为( ) 答案:B 1 2 3 43.经过点M(-2,3),倾斜角为 的直线l的参数方程是 .?1 2 3 44.导学号64470031已知直线l:x+y-1=0与抛物线y=x2交于A,B两点,求线段AB的长和点M(-1,2)到A,B两点的距离之积.
同课章节目录
