高中数学北师大版选修4-5课件:第二章 几个重要的不等式 本章整合 :26张PPT
文档属性
| 名称 | 高中数学北师大版选修4-5课件:第二章 几个重要的不等式 本章整合 :26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 667.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-13 00:00:00 | ||
图片预览








文档简介
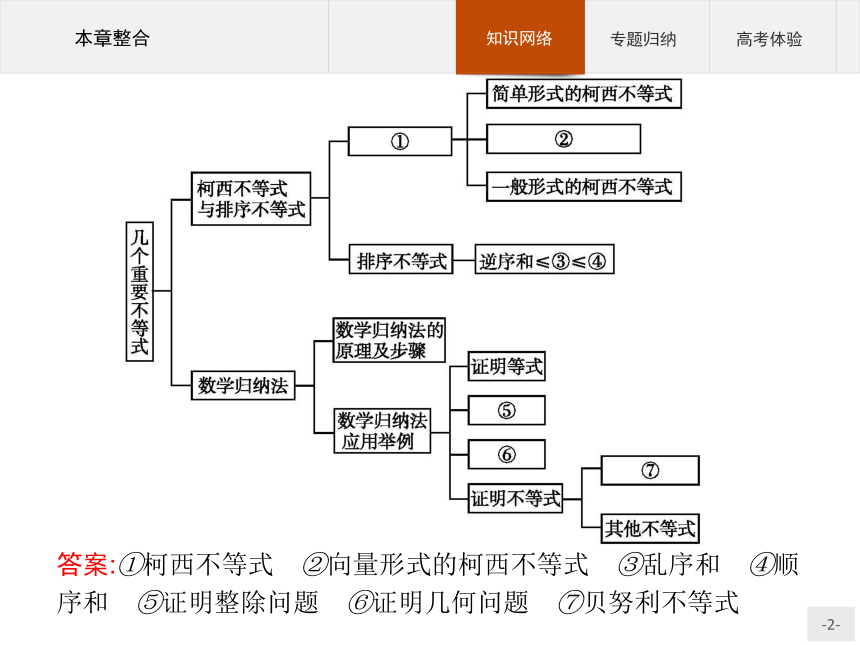
课件26张PPT。本章整合答案:①柯西不等式 ②向量形式的柯西不等式 ③乱序和 ④顺序和 ⑤证明整除问题 ⑥证明几何问题 ⑦贝努利不等式 专题一专题二专题三专题一 柯西不等式的应用
2.利用柯西不等式证明其他不等式的关键是构造两组数,并向着柯西不等式的形式进行转化,运用时要注意体会拼凑和变形技巧.
3.利用柯西不等式证明不等式,特别是求最值时要注意等号是否成立.专题一专题二专题三专题一专题二专题三证明因为a+2b+c=1,a2+b2+c2=1,
所以a+2b=1-c,a2+b2=1-c2.
由柯西不等式可得(12+22)(a2+b2)≥(a+2b)2,
即5(1-c2)≥(1-c)2.
整理得3c2-c-2≤0,专题一专题二专题三专题二 排序不等式的应用
1.在利用排序不等式证明不等式时,首先考虑构造出两个合适的有序数组,并能根据需要进行恰当地组合,这需要结合题目的已知条件及待证不等式的结构特点进行合理选择.
2.根据排序不等式的特点,与多变量间的大小顺序有关的不等式问题,利用排序不等式解决往往很简捷.
3.利用排序不等式求最值时,也要关注等号成立的条件,不能忽略.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题三 数学归纳法的应用
利用数学归纳法证明数列不等式和构造函数利用单调性解决数列中的不等关系是高考重点.在证明不等式时注意以下几点:
(1)在从n=k到n=k+1的过程中,应分析清楚不等式两端项数的变化,也就是认清不等式的结构特征.
(2)对n=k+1中的式子进行等价变形,要用上n=k时的假设.
(3)活用起点位置.
(4)有的试题需先作等价变换.专题一专题二专题三 分析注意到这是与正整数n有关的命题,可考虑用数学归纳法证明. 专题一专题二专题三专题一专题二专题三变式训练3求证:2n+2>n2,n∈N+.
证明(1)当n=1时,左边=21+2=4,右边=1,左边>右边;
当n=2时,左边=22+2=6,右边=22=4,所以左边>右边;
当n=3时,左边=23+2=10,右边=32=9,所以左边>右边.因此当n=1,2,3时,不等式成立.
(2)假设当n=k(k≥3,且k∈N+)时,不等式成立,即2k+2>k2.
则当n=k+1时,2k+1+2=2·2k+2=2(2k+2)-2>2k2-2=k2+2k+1+k2-2k-3=(k2+2k+1)+(k+1)(k-3)≥k2+2k+1=(k+1)2.
所以2k+1+2>(k+1)2.
故当n=k+1时,原不等式也成立.
根据(1)(2)可知,原不等式对于任何n∈N+都成立.2341562341562341562341563.(2017江苏高考)已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明:ac+bd≤8.
证明由柯西不等式可得:(ac+bd)2≤(a2+b2)(c2+d2).
因为a2+b2=4,c2+d2=16,
所以(ac+bd)2≤64,
因此ac+bd≤8.234156考点2:数学归纳法的应用
4.(2015安徽高考)设n∈N+,xn是曲线y=x2n+2+1在点(1,2)处的切线与x轴交点的横坐标.
(1)求数列{xn}的通项公式;234156234156解(1)f(x)的定义域为(-∞,+∞),f'(x)=1-ex.
当f'(x)>0,即x<0时,f(x)单调递增;
当f'(x)<0,即x>0时,f(x)单调递减.
故f(x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞).
当x>0时,f(x)(1)0234156解(1)用数学归纳法证明:xn>0.
当n=1时,x1=1>0,
假设n=k时,xk>0,
那么n=k+1时,若xk+1≤0,
则00.
因此xn>0(n∈N+).
所以xn=xn+1+ln(1+xn+1)>xn+1.
因此0
2.利用柯西不等式证明其他不等式的关键是构造两组数,并向着柯西不等式的形式进行转化,运用时要注意体会拼凑和变形技巧.
3.利用柯西不等式证明不等式,特别是求最值时要注意等号是否成立.专题一专题二专题三专题一专题二专题三证明因为a+2b+c=1,a2+b2+c2=1,
所以a+2b=1-c,a2+b2=1-c2.
由柯西不等式可得(12+22)(a2+b2)≥(a+2b)2,
即5(1-c2)≥(1-c)2.
整理得3c2-c-2≤0,专题一专题二专题三专题二 排序不等式的应用
1.在利用排序不等式证明不等式时,首先考虑构造出两个合适的有序数组,并能根据需要进行恰当地组合,这需要结合题目的已知条件及待证不等式的结构特点进行合理选择.
2.根据排序不等式的特点,与多变量间的大小顺序有关的不等式问题,利用排序不等式解决往往很简捷.
3.利用排序不等式求最值时,也要关注等号成立的条件,不能忽略.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题三 数学归纳法的应用
利用数学归纳法证明数列不等式和构造函数利用单调性解决数列中的不等关系是高考重点.在证明不等式时注意以下几点:
(1)在从n=k到n=k+1的过程中,应分析清楚不等式两端项数的变化,也就是认清不等式的结构特征.
(2)对n=k+1中的式子进行等价变形,要用上n=k时的假设.
(3)活用起点位置.
(4)有的试题需先作等价变换.专题一专题二专题三 分析注意到这是与正整数n有关的命题,可考虑用数学归纳法证明. 专题一专题二专题三专题一专题二专题三变式训练3求证:2n+2>n2,n∈N+.
证明(1)当n=1时,左边=21+2=4,右边=1,左边>右边;
当n=2时,左边=22+2=6,右边=22=4,所以左边>右边;
当n=3时,左边=23+2=10,右边=32=9,所以左边>右边.因此当n=1,2,3时,不等式成立.
(2)假设当n=k(k≥3,且k∈N+)时,不等式成立,即2k+2>k2.
则当n=k+1时,2k+1+2=2·2k+2=2(2k+2)-2>2k2-2=k2+2k+1+k2-2k-3=(k2+2k+1)+(k+1)(k-3)≥k2+2k+1=(k+1)2.
所以2k+1+2>(k+1)2.
故当n=k+1时,原不等式也成立.
根据(1)(2)可知,原不等式对于任何n∈N+都成立.2341562341562341562341563.(2017江苏高考)已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明:ac+bd≤8.
证明由柯西不等式可得:(ac+bd)2≤(a2+b2)(c2+d2).
因为a2+b2=4,c2+d2=16,
所以(ac+bd)2≤64,
因此ac+bd≤8.234156考点2:数学归纳法的应用
4.(2015安徽高考)设n∈N+,xn是曲线y=x2n+2+1在点(1,2)处的切线与x轴交点的横坐标.
(1)求数列{xn}的通项公式;234156234156解(1)f(x)的定义域为(-∞,+∞),f'(x)=1-ex.
当f'(x)>0,即x<0时,f(x)单调递增;
当f'(x)<0,即x>0时,f(x)单调递减.
故f(x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞).
当x>0时,f(x)
当n=1时,x1=1>0,
假设n=k时,xk>0,
那么n=k+1时,若xk+1≤0,
则0
因此xn>0(n∈N+).
所以xn=xn+1+ln(1+xn+1)>xn+1.
因此0
同课章节目录
