高中数学北师大版选修4-4课件:1.1.2 平面直角坐标轴中的伸缩变换 :20张PPT
文档属性
| 名称 | 高中数学北师大版选修4-4课件:1.1.2 平面直角坐标轴中的伸缩变换 :20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-13 15:56:23 | ||
图片预览








文档简介
课件20张PPT。1.2 平面直角坐标轴中的伸缩变换平面直角坐标轴中的伸缩变换
在平面直角坐标系中进行伸缩变换,即改变x轴或y轴的单位长度,将会对图形产生影响.名师点拨对平面直角坐标轴中伸缩变换的理解
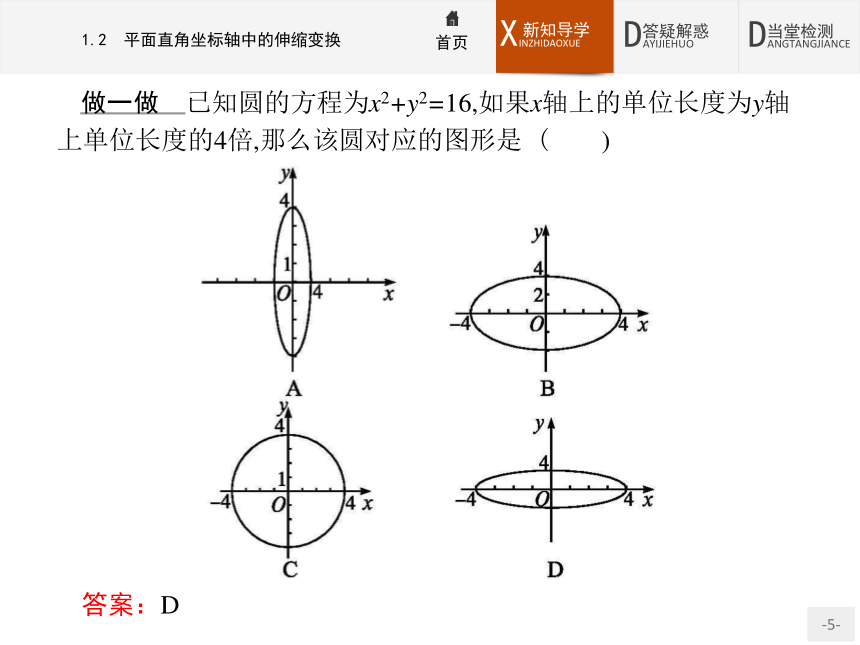
在平面直角坐标系中进行伸缩变换的特点是坐标系和图形发生了改变.如在下列平面直角坐标系中,分别作出f(x,y)=0的图形:(1)x轴与y轴具有相同的单位长度;(2)x轴上的单位长度为y轴上单位长度的k倍;(3)x轴上的单位长度为y轴上单位长度的 倍.第(1)种坐标系中的意思是x轴与y轴上的单位长度一样,f(x,y)=0的图形就是我们以前学过的平面直角坐标系中f(x,y)=0的图形;第(2)种坐标系中的意思是如果x轴上的单位长度保持不变,y轴上的单位长度缩小为原来的 ,那么此时f(x,y)=0表示的图形与第(1)种坐标系中的图形是不同的;第(3)种坐标系中的意思是如果y轴上的单位长度保持不变,x轴上的单位长度缩小为原来的 ,那么此时f(x,y)=0表示的图形与第(1)种坐标系中的图形也是不同的.做一做 已知圆的方程为x2+y2=16,如果x轴上的单位长度为y轴上单位长度的4倍,那么该圆对应的图形是 ( )?答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)在平面直角坐标系中,直线通过伸缩变换还是直线. ( )
(2)在平面直角坐标系中,通过伸缩变换可以把圆变成椭圆. ( )
(3)在平面直角坐标系中,通过伸缩变换可以把双曲线变成抛物线. ( )√ √ × 探究一探究二椭圆在平面直角坐标系中的伸缩变换?
【例1】 在下列平面直角坐标系中,分别作出椭圆 的图形.
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.
分析:先按要求改变x轴或y轴的单位长度,建立平面直角坐标系,再在新坐标系中作出图形.探究一探究二探究一探究二反思感悟在平面直角坐标系中,改变x轴或y轴的单位长度会对图探究一探究二变式训练1 将曲线C按伸缩变换公式 变换得到曲线方程x'2+y'2=1,则曲线C的方程为( )?解析:将 代入x'2+y'2=1,可得到关于x,y的式子,即为曲线C的方程4x2+9y2=1.
答案:D探究一探究二双曲线在平面直角坐标系中的伸缩变换 ?
【例2】 在下列平面直角坐标系中,分别作出双曲线 的图形:
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.解:(1)建立平面直角坐标系,使x轴与y轴具有相同的单位长度,
的图形如下图.探究一探究二探究一探究二反思感悟一般地,在平面直角坐标系中,经过伸缩变换,直线伸缩后仍是直线,双曲线伸缩后仍是双曲线,抛物线伸缩后仍是抛物线,而椭圆伸缩后可能是椭圆或圆.探究一探究二变式训练2 将双曲线C经过伸缩变换 后对应图形的方程为x2-y2=1,则双曲线C的焦点坐标为 .?1 2 3 4 5答案:B 1 2 3 4 52.将直线x+y=1变换为直线2x+3y=6的一个伸缩变换为( )答案:A 1 2 3 4 53.一个平行四边形经过平面直角坐标轴中的伸缩变换后,其图形是 .?
答案:平行四边形1 2 3 4 54.设平面上的伸缩变换的坐标表达式为 则在这一坐标变换下正弦曲线y=sin x的方程变为 .?答案:y'=3sin 2x‘ 1 2 3 4 55.在下列平面直角坐标系中,分别作出以点O'(2,2)为圆心,以1为半径的圆:
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.
解:(1)建立平面直角坐标系使x轴与y轴具有相同的单位长度,以点O'(2,2)为圆心,以1为半径的圆,如图:1 2 3 4 5(2)如果x轴上的单位长度保持不变,y轴上的单位长度缩小为原来的 ,那么以点O'(2,2)为圆心,以1为半径的圆的图形为:(3)如果y轴上的单位长度保持不变,x轴上的单位长度缩小为原来的 ,那么以点O'(2,2)为圆心,以1为半径的圆的图形为:
在平面直角坐标系中进行伸缩变换,即改变x轴或y轴的单位长度,将会对图形产生影响.名师点拨对平面直角坐标轴中伸缩变换的理解
在平面直角坐标系中进行伸缩变换的特点是坐标系和图形发生了改变.如在下列平面直角坐标系中,分别作出f(x,y)=0的图形:(1)x轴与y轴具有相同的单位长度;(2)x轴上的单位长度为y轴上单位长度的k倍;(3)x轴上的单位长度为y轴上单位长度的 倍.第(1)种坐标系中的意思是x轴与y轴上的单位长度一样,f(x,y)=0的图形就是我们以前学过的平面直角坐标系中f(x,y)=0的图形;第(2)种坐标系中的意思是如果x轴上的单位长度保持不变,y轴上的单位长度缩小为原来的 ,那么此时f(x,y)=0表示的图形与第(1)种坐标系中的图形是不同的;第(3)种坐标系中的意思是如果y轴上的单位长度保持不变,x轴上的单位长度缩小为原来的 ,那么此时f(x,y)=0表示的图形与第(1)种坐标系中的图形也是不同的.做一做 已知圆的方程为x2+y2=16,如果x轴上的单位长度为y轴上单位长度的4倍,那么该圆对应的图形是 ( )?答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)在平面直角坐标系中,直线通过伸缩变换还是直线. ( )
(2)在平面直角坐标系中,通过伸缩变换可以把圆变成椭圆. ( )
(3)在平面直角坐标系中,通过伸缩变换可以把双曲线变成抛物线. ( )√ √ × 探究一探究二椭圆在平面直角坐标系中的伸缩变换?
【例1】 在下列平面直角坐标系中,分别作出椭圆 的图形.
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.
分析:先按要求改变x轴或y轴的单位长度,建立平面直角坐标系,再在新坐标系中作出图形.探究一探究二探究一探究二反思感悟在平面直角坐标系中,改变x轴或y轴的单位长度会对图探究一探究二变式训练1 将曲线C按伸缩变换公式 变换得到曲线方程x'2+y'2=1,则曲线C的方程为( )?解析:将 代入x'2+y'2=1,可得到关于x,y的式子,即为曲线C的方程4x2+9y2=1.
答案:D探究一探究二双曲线在平面直角坐标系中的伸缩变换 ?
【例2】 在下列平面直角坐标系中,分别作出双曲线 的图形:
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.解:(1)建立平面直角坐标系,使x轴与y轴具有相同的单位长度,
的图形如下图.探究一探究二探究一探究二反思感悟一般地,在平面直角坐标系中,经过伸缩变换,直线伸缩后仍是直线,双曲线伸缩后仍是双曲线,抛物线伸缩后仍是抛物线,而椭圆伸缩后可能是椭圆或圆.探究一探究二变式训练2 将双曲线C经过伸缩变换 后对应图形的方程为x2-y2=1,则双曲线C的焦点坐标为 .?1 2 3 4 5答案:B 1 2 3 4 52.将直线x+y=1变换为直线2x+3y=6的一个伸缩变换为( )答案:A 1 2 3 4 53.一个平行四边形经过平面直角坐标轴中的伸缩变换后,其图形是 .?
答案:平行四边形1 2 3 4 54.设平面上的伸缩变换的坐标表达式为 则在这一坐标变换下正弦曲线y=sin x的方程变为 .?答案:y'=3sin 2x‘ 1 2 3 4 55.在下列平面直角坐标系中,分别作出以点O'(2,2)为圆心,以1为半径的圆:
(1)x轴与y轴具有相同的单位长度;
(2)x轴上的单位长度为y轴上单位长度的2倍;
(3)x轴上的单位长度为y轴上单位长度的 倍.
解:(1)建立平面直角坐标系使x轴与y轴具有相同的单位长度,以点O'(2,2)为圆心,以1为半径的圆,如图:1 2 3 4 5(2)如果x轴上的单位长度保持不变,y轴上的单位长度缩小为原来的 ,那么以点O'(2,2)为圆心,以1为半径的圆的图形为:(3)如果y轴上的单位长度保持不变,x轴上的单位长度缩小为原来的 ,那么以点O'(2,2)为圆心,以1为半径的圆的图形为:
同课章节目录
