高中数学人教A版选修4-1课件:本讲整合1 :25张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:本讲整合1 :25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 798.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-13 00:00:00 | ||
图片预览






文档简介
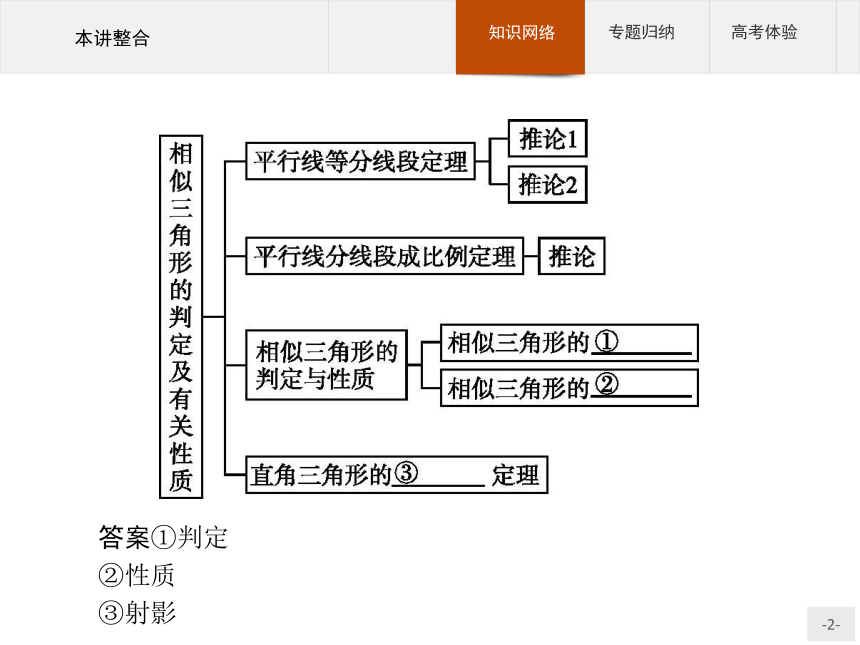
课件25张PPT。本讲整合答案①判定
②性质
③射影专题一专题二专题三专题一:平行线分线段成比例定理及其应用
1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.
2.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.专题一专题二专题三例1如图,在四边形ABCD中,AC,BD交于点O,过点O作AB的平行线,与AD,BC分别交于点E,F,与CD的延长线交于点K,则解析延长CK,BA,设它们交于点H, 专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题二:相似三角形的判定与性质
1.相似三角形的定义
对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).
2.相似三角形的判定
(1)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
(2)两角对应相等的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(4)三边对应成比例的两个三角形相似.专题一专题二专题三3.直角三角形相似的判定
(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
4.相似三角形的性质
(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(2)相似三角形周长的比等于相似比.
(3)相似三角形面积的比等于相似比的平方.
(4)相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.专题一专题二专题三例2如图,在梯形ABCD中,AB∥CD,且AB=2CD,点E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM的长.
分析对于(1),可通过证明CB∥DE并结合相似三角形的判定定理证明;(2)可由(1)结合相似三角形的性质求解.专题一专题二专题三(1)证明∵点E是AB的中点,∴AB=2BE.
又AB=2CD,∴CD=EB.
∵AB∥CD,∴四边形CBED是平行四边形.
∴CB∥DE,∴∠DEM=∠BFM,∠EDM=∠FBM,
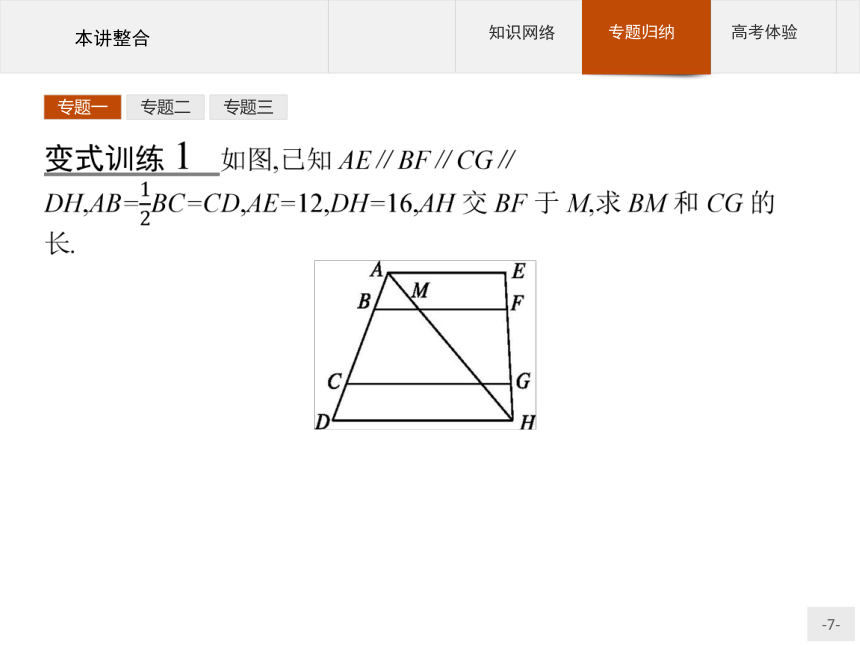
∴△EDM∽△FBM.专题一专题二专题三专题一专题二专题三变式训练2 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:?
(1)△ABC≌△DCB;
(2)DE·DC=AE·BD.
证明(1)∵四边形ABCD是等腰梯形,∴AC=DB,AB=DC.又BC=CB,∴△ABC≌△DCB.
(2)由(1)知,△ABC≌△DCB,
∴∠ACB=∠DBC,∠ABC=∠DCB.
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC.
又ED∥AC,∴∠EDA=∠DAC.
∴∠EDA=∠DBC,∠EAD=∠DCB.
∴△ADE∽△CBD,∴DE∶BD=AE∶CD.
∴DE·DC=AE·BD.专题一专题二专题三专题三:直角三角形的射影定理及其应用
直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.专题一专题二专题三例3如图所示,在Rt△ABC中有正方形DEFG,点D,G分别在AB,AC上,点E,F在斜边BC上,求证:EF2=BE·FC.
?
证明如图所示,过点A作AH⊥BC于点H,
则DE∥AH∥GF. 专题一专题二专题三专题一专题二专题三专题一专题二专题三变式训练3 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于点E,EF⊥AB于点F,若BD·DF=4,则CE= .? 考点1考点2考点1:相似三角形的判定与性质
1.(2013·陕西高考)如图,弦AB与CD相交于☉O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE= .?考点1考点22.(2014·陕西高考)如图,△ABC中,BC=6,以BC为
直径的半圆分别交AB,AC于点E,F,若AC=2AE,
则EF= .?解析由已知得四边形BCFE为圆的内接四边形,因此∠AEF=∠ACB,∠AFE=∠ABC,所以△AEF∽△ACB,于是有
,而AC=2AE,BC=6,所以EF=3.
答案3考点1考点2考点1考点24.(2016·江苏高考)
如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.
求证:∠EDC=∠ABD.
证明在△ADB与△ABC中,因为∠ABC=90°,BD⊥AC,∠A为公共角,所以△ADB∽△ABC,
于是∠ABD=∠C.
在Rt△BDC中,因为E是BC的中点,
所以ED=EC,从而∠EDC=∠C.
所以∠EDC=∠ABD.考点1考点2考点2:射影定理
5.
(2013·广东高考)如图,在矩形ABCD中,AB= ,BC=3,BE⊥AC,垂足为E,则ED= .?考点1考点2
②性质
③射影专题一专题二专题三专题一:平行线分线段成比例定理及其应用
1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.
2.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.专题一专题二专题三例1如图,在四边形ABCD中,AC,BD交于点O,过点O作AB的平行线,与AD,BC分别交于点E,F,与CD的延长线交于点K,则解析延长CK,BA,设它们交于点H, 专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题二:相似三角形的判定与性质
1.相似三角形的定义
对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).
2.相似三角形的判定
(1)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
(2)两角对应相等的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(4)三边对应成比例的两个三角形相似.专题一专题二专题三3.直角三角形相似的判定
(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
4.相似三角形的性质
(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(2)相似三角形周长的比等于相似比.
(3)相似三角形面积的比等于相似比的平方.
(4)相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.专题一专题二专题三例2如图,在梯形ABCD中,AB∥CD,且AB=2CD,点E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM的长.
分析对于(1),可通过证明CB∥DE并结合相似三角形的判定定理证明;(2)可由(1)结合相似三角形的性质求解.专题一专题二专题三(1)证明∵点E是AB的中点,∴AB=2BE.
又AB=2CD,∴CD=EB.
∵AB∥CD,∴四边形CBED是平行四边形.
∴CB∥DE,∴∠DEM=∠BFM,∠EDM=∠FBM,
∴△EDM∽△FBM.专题一专题二专题三专题一专题二专题三变式训练2 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:?
(1)△ABC≌△DCB;
(2)DE·DC=AE·BD.
证明(1)∵四边形ABCD是等腰梯形,∴AC=DB,AB=DC.又BC=CB,∴△ABC≌△DCB.
(2)由(1)知,△ABC≌△DCB,
∴∠ACB=∠DBC,∠ABC=∠DCB.
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC.
又ED∥AC,∴∠EDA=∠DAC.
∴∠EDA=∠DBC,∠EAD=∠DCB.
∴△ADE∽△CBD,∴DE∶BD=AE∶CD.
∴DE·DC=AE·BD.专题一专题二专题三专题三:直角三角形的射影定理及其应用
直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.专题一专题二专题三例3如图所示,在Rt△ABC中有正方形DEFG,点D,G分别在AB,AC上,点E,F在斜边BC上,求证:EF2=BE·FC.
?
证明如图所示,过点A作AH⊥BC于点H,
则DE∥AH∥GF. 专题一专题二专题三专题一专题二专题三专题一专题二专题三变式训练3 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于点E,EF⊥AB于点F,若BD·DF=4,则CE= .? 考点1考点2考点1:相似三角形的判定与性质
1.(2013·陕西高考)如图,弦AB与CD相交于☉O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE= .?考点1考点22.(2014·陕西高考)如图,△ABC中,BC=6,以BC为
直径的半圆分别交AB,AC于点E,F,若AC=2AE,
则EF= .?解析由已知得四边形BCFE为圆的内接四边形,因此∠AEF=∠ACB,∠AFE=∠ABC,所以△AEF∽△ACB,于是有
,而AC=2AE,BC=6,所以EF=3.
答案3考点1考点2考点1考点24.(2016·江苏高考)
如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.
求证:∠EDC=∠ABD.
证明在△ADB与△ABC中,因为∠ABC=90°,BD⊥AC,∠A为公共角,所以△ADB∽△ABC,
于是∠ABD=∠C.
在Rt△BDC中,因为E是BC的中点,
所以ED=EC,从而∠EDC=∠C.
所以∠EDC=∠ABD.考点1考点2考点2:射影定理
5.
(2013·广东高考)如图,在矩形ABCD中,AB= ,BC=3,BE⊥AC,垂足为E,则ED= .?考点1考点2
