高中数学人教A版选修4-1课件:1.3.1 相似三角形的判定 :35张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:1.3.1 相似三角形的判定 :35张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-13 00:00:00 | ||
图片预览









文档简介
课件35张PPT。三 相似三角形的判定及性质1.相似三角形的判定121.相似三角形
(1)相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形.
(2)相似比:相似三角形对应边的比值叫做相似比(或相似系数).
(3)表示方法:两个三角形相似,用符号“∽”表示.例如:△ABC与△A'B'C'相似,记为△ABC∽△A'B'C'.312做一做1 若△ABC∽△A1B1C1,则下列结论中正确的是( )?
A.AB=A1B1 B.∠ABC=∠A1B1C1
答案B3122.相似三角形的判定
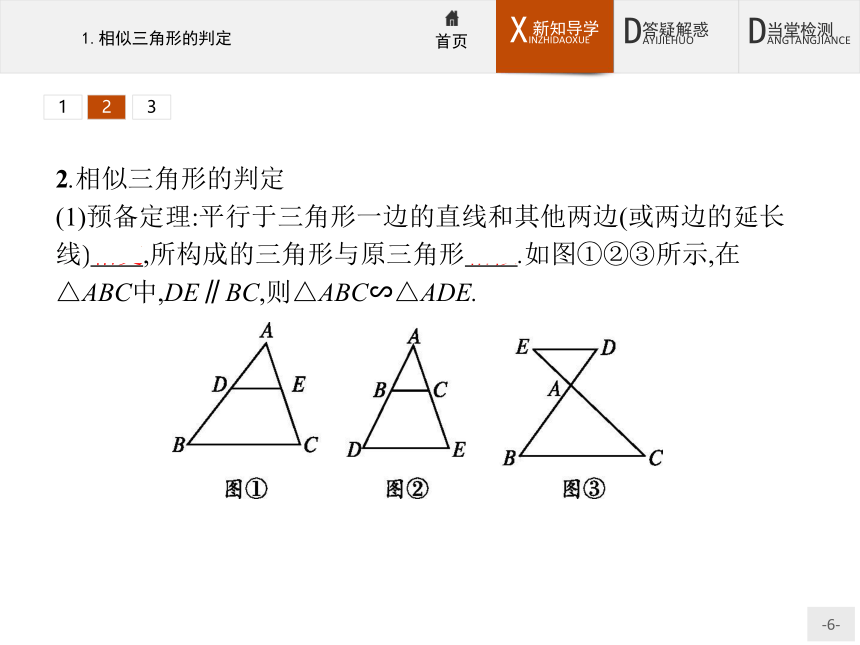
(1)预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.如图①②③所示,在△ABC中,DE∥BC,则△ABC∽△ADE.312(2)判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.
(3)引理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
(4)判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.
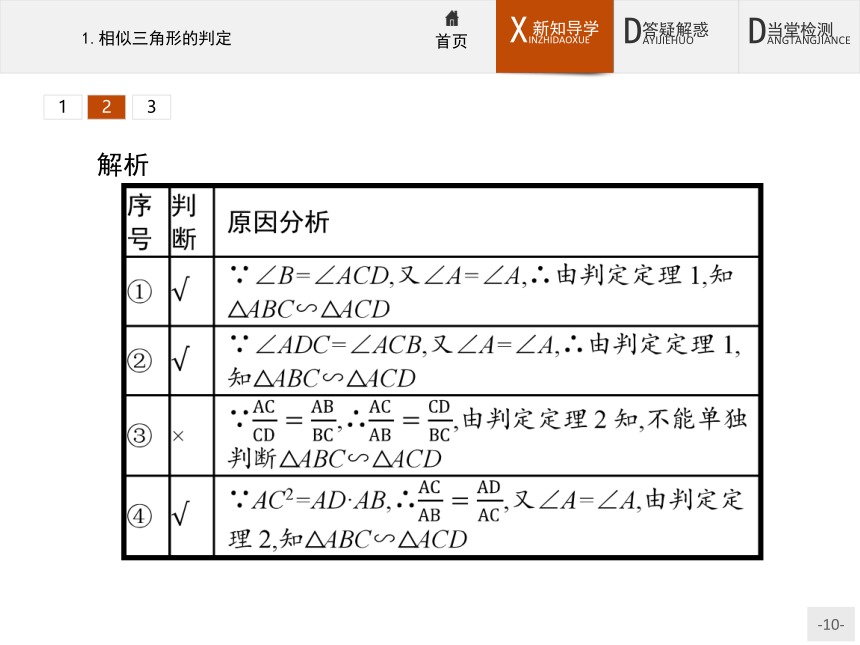
(5)判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.312312做一做2 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠
的个数为( )?
A.1 B.2 C.3 D.4312解析 答案C 31233.直角三角形相似的判定
(1)定理1:如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)定理2:如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)定理3:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形
相似.123123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)有两边对应成比例及一个角相等的两个三角形相似. ( )
(2)有三边分别对应平行的两个三角形相似. ( )
(3)有两边成比例的两个等腰三角形相似. ( )
(4)有两边及一边上的高对应成比例的两个三角形相似. ( )
(5)如果两个直角三角形中有一个内角相等,那么它们一定相似. ( )
答案(1)× (2)√ (3)× (4)× (5)×探究一探究二探究三思维辨析探究一三角形相似的定义?
【例1】如图所示,在△ABC中,AB=AC,
∠A=36°,BD是∠B的平分线,
试证明:AD2=DC·AC.
分析顶角是36°的等腰三角形,它的底角是72°,而BD是底角的平分线,所以∠CBD=36°,则可推出△ABC∽△BCD,进而由相似三角形对应边成比例推出线段之间的比例关系.
证明∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.
又BD平分∠ABC,∴∠ABD=∠CBD=36°.
∴AD=BD=BC,且△ABC∽△BCD.
∴BC∶AB=CD∶BC.
∴BC2=AB·CD.又AD=BC,AB=AC,
∴AD2=CD·AC.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练1 如图,在平行四边形ABCD中,点E在DC上,若DE∶EC=1∶2,则BF∶BE= .?
解析∵DE∶EC=1∶2,
∴DC∶EC=3∶2,∴AB∶EC=3∶2.
∵AB∥EC,∴△ABF∽△CEF,
答案3∶5探究一探究二探究三思维辨析探究二三角形相似的判定?
【例2】 如图所示,已知在△ABC中,AB=AC,AD是BC边上的中线,CF∥BA,BF交AD于点P,交AC于点E.求证:△PCE∽△PFC.
分析由于△PCE和△PFC有公共角,因此只需再证得另一组对应角相等即可.探究一探究二探究三思维辨析证明如图,在△ABC中,∵AB=AC,D为BC的中点,
∴AD垂直平分BC.
∴PB=PC,∠1=∠2.
∵AB=AC,∴∠ABC=∠ACB.
∴∠ABC-∠1=∠ACB-∠2,即∠3=∠4.
∵CF∥AB,∴∠3=∠F,∴∠4=∠F.
又∠EPC=∠CPF,
故△PCE∽△PFC.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练2?如图,在Rt△ABC中,∠BAC=90°,BM是AC边上的中线,AD⊥BM,垂足是点D.求证:△MCD∽△MBC.探究一探究二探究三思维辨析探究三直角三角形相似的判定?
【例3】 如图所示,直线EF分别交AB,AC于点F,E,交BC的延长线于点D,AC⊥BC于点C,且AB·CD=DE·AC.求证:AE·CE=DE·EF.
分析先证△ACB∽△DCE,再证△AEF∽△DEC即可.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3 如图,已知在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.? 探究一探究二探究三思维辨析对相似三角形的判定定理理解不准确致误
典例如图所示,在△ABC和△A1B1C1中,∠1=∠2,∠3=∠4 探究一探究二探究三思维辨析三角形的判定定理可知△ABD∽△A1B1D1,△ACD∽△A1C1D1,从而△ABC∽△A1B1C1.
正解如图所示,过点C作CE∥AB,交AD的延长线于点E,过点C1作C1E1∥A1B1,交A1D1的延长线于点E1,则∠E=∠1,∠E1=∠3.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练 如图所示,O是△ABC外一点,D,E,F分别是OA,OB,OC的中点,求证:△DEF∽△ABC.?123451.如图所示,AB=8,AD=3,AC=6,当AE=( )时,可推出△ADE∽△ACB.12345123453.如图所示,DE∥BC,则△ADE∽△ ,∠A=∠ ,∠ADE=∠ ,∠AED=∠ .若AD=5,DB=3,则△ADE与△ABC的相似比是 .?123454.如图,BD,CE是△ABC的高,BD,CE交于点F,则图中所有与△ACE相似的三角形有 .?
解析Rt△ACE与Rt△FCD和Rt△ABD各有一个公共角,因而它们均相似.又易知∠BFE=∠A,
故Rt△ACE∽Rt△FBE.
答案△FCD,△FBE,△ABD123455.如图,在梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM的长.12345(1)证明因为E是AB的中点,
所以AB=2EB.
因为AB=2CD,所以CD=EB.
又AB∥CD,所以四边形CBED是平行四边形.
所以CB∥DE,
所以∠DEM=∠BFM,∠EDM=∠FBM,
所以△EDM∽△FBM.
(1)相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形.
(2)相似比:相似三角形对应边的比值叫做相似比(或相似系数).
(3)表示方法:两个三角形相似,用符号“∽”表示.例如:△ABC与△A'B'C'相似,记为△ABC∽△A'B'C'.312做一做1 若△ABC∽△A1B1C1,则下列结论中正确的是( )?
A.AB=A1B1 B.∠ABC=∠A1B1C1
答案B3122.相似三角形的判定
(1)预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.如图①②③所示,在△ABC中,DE∥BC,则△ABC∽△ADE.312(2)判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.
(3)引理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
(4)判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.
(5)判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.312312做一做2 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠
的个数为( )?
A.1 B.2 C.3 D.4312解析 答案C 31233.直角三角形相似的判定
(1)定理1:如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)定理2:如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)定理3:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形
相似.123123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)有两边对应成比例及一个角相等的两个三角形相似. ( )
(2)有三边分别对应平行的两个三角形相似. ( )
(3)有两边成比例的两个等腰三角形相似. ( )
(4)有两边及一边上的高对应成比例的两个三角形相似. ( )
(5)如果两个直角三角形中有一个内角相等,那么它们一定相似. ( )
答案(1)× (2)√ (3)× (4)× (5)×探究一探究二探究三思维辨析探究一三角形相似的定义?
【例1】如图所示,在△ABC中,AB=AC,
∠A=36°,BD是∠B的平分线,
试证明:AD2=DC·AC.
分析顶角是36°的等腰三角形,它的底角是72°,而BD是底角的平分线,所以∠CBD=36°,则可推出△ABC∽△BCD,进而由相似三角形对应边成比例推出线段之间的比例关系.
证明∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.
又BD平分∠ABC,∴∠ABD=∠CBD=36°.
∴AD=BD=BC,且△ABC∽△BCD.
∴BC∶AB=CD∶BC.
∴BC2=AB·CD.又AD=BC,AB=AC,
∴AD2=CD·AC.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练1 如图,在平行四边形ABCD中,点E在DC上,若DE∶EC=1∶2,则BF∶BE= .?
解析∵DE∶EC=1∶2,
∴DC∶EC=3∶2,∴AB∶EC=3∶2.
∵AB∥EC,∴△ABF∽△CEF,
答案3∶5探究一探究二探究三思维辨析探究二三角形相似的判定?
【例2】 如图所示,已知在△ABC中,AB=AC,AD是BC边上的中线,CF∥BA,BF交AD于点P,交AC于点E.求证:△PCE∽△PFC.
分析由于△PCE和△PFC有公共角,因此只需再证得另一组对应角相等即可.探究一探究二探究三思维辨析证明如图,在△ABC中,∵AB=AC,D为BC的中点,
∴AD垂直平分BC.
∴PB=PC,∠1=∠2.
∵AB=AC,∴∠ABC=∠ACB.
∴∠ABC-∠1=∠ACB-∠2,即∠3=∠4.
∵CF∥AB,∴∠3=∠F,∴∠4=∠F.
又∠EPC=∠CPF,
故△PCE∽△PFC.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练2?如图,在Rt△ABC中,∠BAC=90°,BM是AC边上的中线,AD⊥BM,垂足是点D.求证:△MCD∽△MBC.探究一探究二探究三思维辨析探究三直角三角形相似的判定?
【例3】 如图所示,直线EF分别交AB,AC于点F,E,交BC的延长线于点D,AC⊥BC于点C,且AB·CD=DE·AC.求证:AE·CE=DE·EF.
分析先证△ACB∽△DCE,再证△AEF∽△DEC即可.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3 如图,已知在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.? 探究一探究二探究三思维辨析对相似三角形的判定定理理解不准确致误
典例如图所示,在△ABC和△A1B1C1中,∠1=∠2,∠3=∠4 探究一探究二探究三思维辨析三角形的判定定理可知△ABD∽△A1B1D1,△ACD∽△A1C1D1,从而△ABC∽△A1B1C1.
正解如图所示,过点C作CE∥AB,交AD的延长线于点E,过点C1作C1E1∥A1B1,交A1D1的延长线于点E1,则∠E=∠1,∠E1=∠3.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练 如图所示,O是△ABC外一点,D,E,F分别是OA,OB,OC的中点,求证:△DEF∽△ABC.?123451.如图所示,AB=8,AD=3,AC=6,当AE=( )时,可推出△ADE∽△ACB.12345123453.如图所示,DE∥BC,则△ADE∽△ ,∠A=∠ ,∠ADE=∠ ,∠AED=∠ .若AD=5,DB=3,则△ADE与△ABC的相似比是 .?123454.如图,BD,CE是△ABC的高,BD,CE交于点F,则图中所有与△ACE相似的三角形有 .?
解析Rt△ACE与Rt△FCD和Rt△ABD各有一个公共角,因而它们均相似.又易知∠BFE=∠A,
故Rt△ACE∽Rt△FBE.
答案△FCD,△FBE,△ABD123455.如图,在梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM的长.12345(1)证明因为E是AB的中点,
所以AB=2EB.
因为AB=2CD,所以CD=EB.
又AB∥CD,所以四边形CBED是平行四边形.
所以CB∥DE,
所以∠DEM=∠BFM,∠EDM=∠FBM,
所以△EDM∽△FBM.
